1 条题解
-
0
自动搬运
来自洛谷,原作者为

Y_B_X
...搬运于
2025-08-24 22:01:25,当前版本为作者最后更新于2022-02-09 11:36:13,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
在 的天幕下,点分治、边分治与虚树的磨合正轰轰烈烈地进行着,似将前路雪封。
正当边分治能以一个 的优势一马当先之际;
殊不知,怀揣着 的三人小队已一举拿下暂时最优解。
他们是谁?不出所料,正是小常数三人组:,树剖,。题意:给定两棵树,边有边权,求 $\mathrm{MAX}\left(\operatorname{dep}_x+\operatorname{dep}_y-\operatorname{dep}_{\operatorname{lca}(x,y)}-\operatorname{\hat {dep}}_{\operatorname{\hat{lca}}(x,y)}\right)$,
对第一棵树进行 ,目标是在每个节点处理出跨过它的所有点对。
由于式子具有良好的对称性,所以重儿子的信息能直接利用,只需在轻子树内查询,每个儿子子树查完后更新信息。
假设目前在处理节点 ,则 ,而 在 的一个轻儿子子树内, 是 之前遍历过的儿子子树内一点(包括重儿子)。
轻子树是允许直接遍历的,所以此时 与 都已知,只需求 $\mathrm{MAX}\left(\operatorname{dep}_y-\operatorname{\hat {dep}}_{\operatorname{\hat{lca}}(x,y)}\right)$
这仅仅与第二棵树有关了,问题转化为一个树上动态加 ,查 $\mathrm{MAX}\left(a_y-\operatorname{dep}_{\operatorname{lca}(x,y)}\right)$
这可以用树剖优化了,上图:
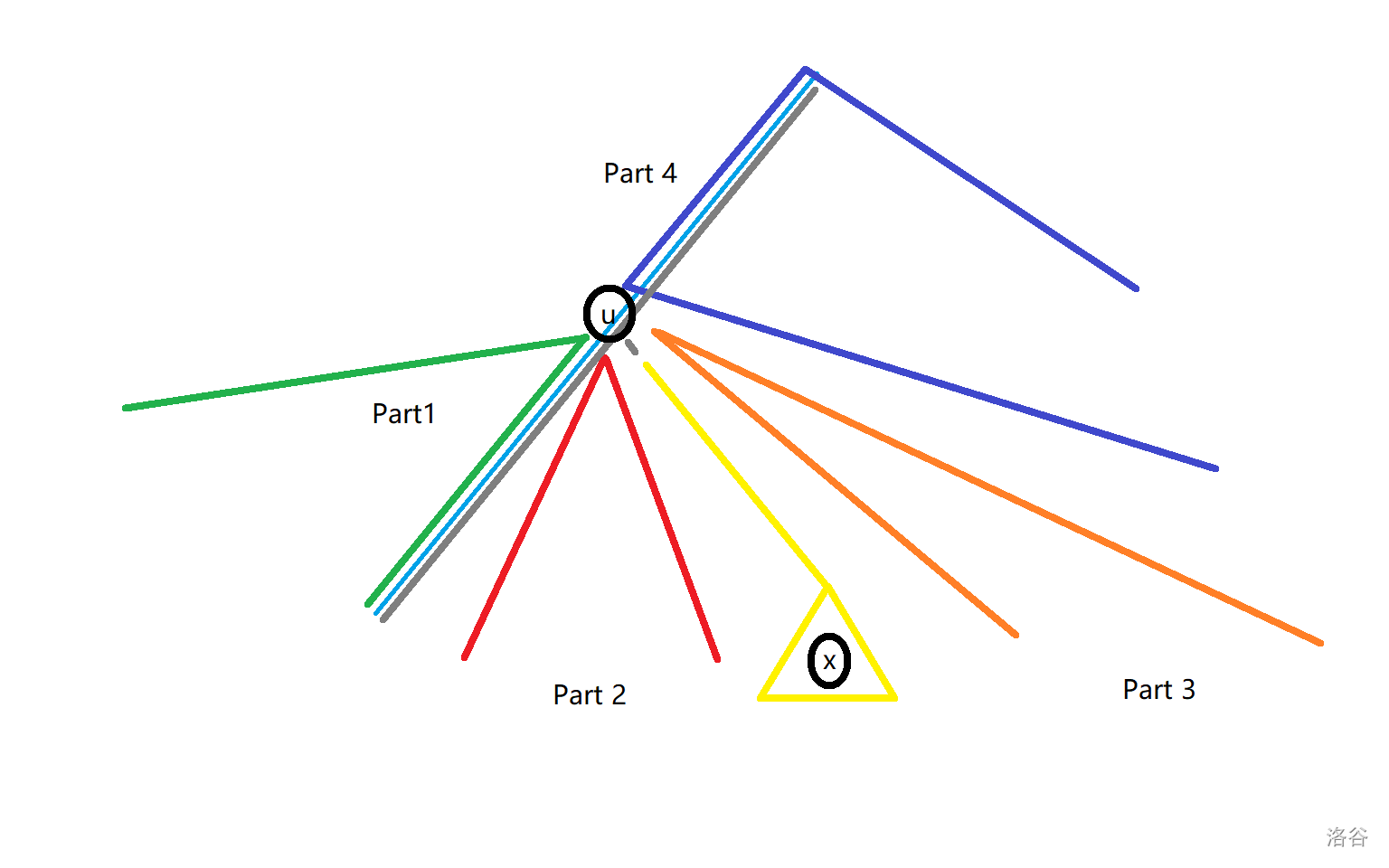
其中 是 跳到的一个重链上一点, 是 子树中除了 一边的两部分, 是重链 上下的部分。
如果 在 中, 只需求这部分的 。
这可以在每次加入 时向上跳链,将信息存在链上 以及点上
而 在 中, 一定是重链上 跳到的位置,在更新 时同样可以存到重链上。
而对于重链以及儿子信息的存储,可以对每条链,每个点开树状数组实现。
查询与更新就此结束,但 还会自带一个删除,似乎树状数组实现不了。
但由于 时时只会处理一个子树,直接在第二棵树把影响的点清除即可。
理论时间复杂度是 ,后面的树剖以及树状数组其实也能用 做到大常数 。
由于外层有 ,十分难卡满,但临时最优解确实出乎意料。
代码:
#include<bits/stdc++.h> #define ll long long using namespace std; const int N=4e5+10; const ll inf=1e18; int n,m,x,y,v,tot;ll res,ans; int to[N<<1],nextn[N<<1],w[N<<1],h[N],edg; int son[N],sz[N],tmp[N];ll d[N]; char ch;bool rf; inline void read(int &x){ x=0;ch=getchar();while(ch<47)ch=getchar(); while(ch>47)x=(x<<1)+(x<<3)+(ch^48),ch=getchar(); } inline void read_(int &x){ x=0;ch=getchar();rf=0;while(ch<47&&ch^'-')ch=getchar(); if(ch=='-')rf=1,ch=getchar(); while(ch>47)x=(x<<1)+(x<<3)+(ch^48),ch=getchar(); if(rf)x=-x; } inline ll max(ll a,ll b){return a>b?a:b;} inline void add(){to[++edg]=y,nextn[edg]=h[x],h[x]=edg,w[edg]=v;} void init(int x,int anc){ int i,y;sz[x]=1; for(i=h[x];y=to[i];i=nextn[i])if(y^anc){ d[y]=d[x]+w[i];init(y,x);sz[x]+=sz[y]; sz[y]>sz[son[x]]?son[x]=y:0; } } #define lowbit(i) i&(-i) struct bit{ ll *t,res;int n;bit()=default; bit(ll *tt,int nn):t(tt),n(nn){for(int i=1;i<=n;++i)t[i]=-inf;} inline void update(int i,ll v){for(;i<=n;i+=lowbit(i))t[i]=max(t[i],v);} inline void inquiry(int i){for(res=-inf;i;i-=lowbit(i))res=max(res,t[i]);} inline void clear(int i){for(;i<=n;i+=lowbit(i))t[i]=-inf;} }; struct the_second_tree{ int x,y,tot,nn,i,edg; int to[N<<1],nextn[N<<1],w[N<<1],h[N],tmp[N],id[N]; int sz[N],son[N],anc[N],top[N],cnum[N],vnum[N]; int crk[N],crk_[N],vrk[N],vrk_[N]; ll up_[N<<1],*upp=up_,dn_[N<<1],*dnn=dn_; ll vl_[N<<1],*vll=vl_,vr_[N<<1],*vrr=vr_; bit up[N],dn[N],vl[N],vr[N]; ll a[N],d[N],res,ax,dx;bool b[N]; inline void add(){to[++edg]=y,nextn[edg]=h[x],h[x]=edg,w[edg]=v;} void dfs(int x,int anc_){ anc[x]=anc_;sz[x]=1;int i,y; for(i=h[x];y=to[i];i=nextn[i])if(y^anc_){ d[y]=d[x]+w[i];dfs(y,x);sz[x]+=sz[y]; sz[y]>sz[son[x]]?son[x]=y:0; } } void init(int x,int anc_,int tp){ top[x]=tp; if(!son[x]){ ++nn;i=0;id[tp]=nn; while(top[x]==tp)++i,crk[x]=i,x=anc[x];cnum[nn]=i; up[nn]=bit(upp,i),upp+=i+1;dn[nn]=bit(dnn,i),dnn+=i+1; } else { init(son[x],x,tp);int i,y,j=0; for(i=h[x];y=to[i];i=nextn[i])if(y^anc_&&y^son[x]) vrk[y]=++j,init(y,x,y);vnum[x]=j; vl[x]=bit(vll,j),vll+=j+1;vr[x]=bit(vrr,j),vrr+=j+1; } } void update(int x){ ax=a[x];b[x]=1; while(x){ y=top[x];i=id[y]; dn[i].update(crk[x],ax); up[i].update(crk_[x],ax-d[x]); x=anc[y]; if(x){ vl[x].update(vrk[y],ax); vr[x].update(vrk_[y],ax); } } } void inquiry(int x){ res=-inf; if(vnum[x]){ vl[x].inquiry(vnum[x]);res=max(res,vl[x].res-d[x]); vr[x].inquiry(vnum[x]);res=max(res,vr[x].res-d[x]); } while(x){ y=top[x];i=id[y]; dn[i].inquiry(crk[x]-1);res=max(res,dn[i].res-d[x]); up[i].inquiry(crk_[x]-1);res=max(res,up[i].res); x=anc[y];b[x]?res=max(res,a[x]-d[x]):0;x=anc[y]; if(x){ vl[x].inquiry(vrk[y]-1);res=max(res,vl[x].res-d[x]); vr[x].inquiry(vrk_[y]-1);res=max(res,vr[x].res-d[x]); } } } void clear(int x){ b[x]=0; while(x){ y=top[x];i=id[y]; dn[i].clear(crk[x]); up[i].clear(crk_[x]); x=anc[y]; if(x){ vl[x].clear(vrk[y]); vr[x].clear(vrk_[y]); } } } void pre_work(){ int i; for(i=1;i^n;++i)read(x),read(y),read_(v),add(),x^=y^=x^=y,add(); dfs(1,0);init(1,0,1); for(i=1;i<=n;++i)crk_[i]=cnum[id[top[i]]]-crk[i]+1; for(i=1;i<=n;++i)if(vrk[i])vrk_[i]=vnum[anc[i]]-vrk[i]+1; } }T; void clear(int x,int anc){ int i,y;T.clear(x); for(i=h[x];y=to[i];i=nextn[i])if(y^anc)clear(y,x); } void dfs(int x,int anc){ int i,y;T.inquiry(x);res=max(res,T.res+d[x]);tmp[++tot]=x; for(i=h[x];y=to[i];i=nextn[i])if(y^anc)dfs(y,x); } void solve(int x,int anc){ int i,y,j; for(i=h[x];y=to[i];i=nextn[i])if(y^anc&&y^son[x])solve(y,x),clear(y,x); if(son[x])solve(son[x],x);res=-inf; for(i=h[x];y=to[i];i=nextn[i])if(y^anc&&y^son[x]){ tot=0;dfs(y,x); for(j=1;j<=tot;++j)T.update(tmp[j]); } T.inquiry(x);res=max(res,T.res+d[x]); T.update(x);ans=max(ans,res-d[x]); } main(){ read(n);register int i; for(i=1;i^n;++i)read(x),read(y),read_(v),add(),x^=y^=x^=y,add(); init(1,0);T.pre_work();for(i=1;i<=n;++i)T.a[i]=d[i]; solve(1,0); for(i=1;i<=n;++i)ans=max(ans,d[i]-T.d[i]); printf("%lld",ans); }
- 1
信息
- ID
- 3494
- 时间
- 4000ms
- 内存
- 512MiB
- 难度
- 7
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
