自动搬运

查看原文

来自洛谷，原作者为

	GKxx 欲买桂花同载酒，终不似，少年游。

搬运于2025-08-24 22:00:56，当前版本为作者最后更新于2018-11-04 00:31:59，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

一道树上背包简单题

状态很好推。设$dp[x][i][0/1][0/1]$表示以$x$为根的子树中共放了$i$个监听装置，其中$x$点放没放装置，$x$点有没有被监听到的方案数（在以$x$为根的子树中除$x$外的其它结点都被监听到了）

不难看出这是一个树上背包，树上背包的转移套路是

$dp[x][i+j]=combine(dp[x][i],dp[v][j])$，其中$v$是$x$的子节点

所以本题的转移也就这样来考虑。把树画成这样，分为$x$侧和$v$侧

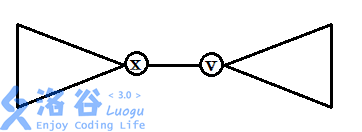
如果您有能力请自行推出方程，跳过这一段

• 如果$x$没被监听，那么$v$一定不能放装置，因此 $dp[x][i+j][0][0]=\sum dp[x][i][0][0]*dp[v][j][0][1]$

• 如果$x$没被监听但是放了装置，$x$侧的状态一定是$dp[x][i][1][0]$，$v$是否被监听无所谓但是一定不能放装置，因此 $dp[x][i+j][1][0]=\sum dp[x][i][1][0]*(dp[v][j][0][0]+dp[v][j][0][1])$

• 如果$x$没放装置但是被监听了，这时候要分情况：

  $x$侧的状态是$dp[x][i][0][1]$，这时候反正$x$已经被监听了，$v$放不放装置都无所谓，但是必须保证$v$是被监听的，所以贡献是$dp[x][i][0][1]*(dp[v][j][0][1]+dp[v][j][1][1])$

  $x$侧的状态是$dp[x][i][0][0]$，这时候监听$x$的重任就要交给$v$了，同时$v$自己必须是被监听的，所以贡献是$dp[x][i][0][0]*dp[v][j][1][1]$

  因此$dp[x][i+j][0][1]=\sum (dp[x][i][0][1]*(dp[v][j][0][1]+dp[v][j][1][1])+dp[x][i][0][0]*dp[v][j][1][1])$

• 如果$x$既放了装置又被监听，同样要分两种情况：

  $x$侧的状态是$dp[x][i][1][0]$，需要让$v$来监听$x$，但是$v$是否被监听无所谓，因为$x$上放了装置可以保证$v$被监听，所以贡献是$dp[x][i][1][0]*(dp[v][j][1][0]+dp[v][j][1][1])$

  $x$侧的状态是$dp[x][i][1][1]$，这时候$x$的所有要求都满足了，$v$怎么样都行，贡献是$dp[x][i][1][1]*(dp[v][j][0][0]+dp[v][j][0][1]+dp[v][j][1][0]+dp[v][j][1][1])$

  因此$dp[x][i+j][1][1]=\sum (dp[x][i][1][0]*(dp[v][j][1][0]+dp[v][j][1][1])+dp[x][i][1][1]*(dp[v][j][0][0]+dp[v][j][0][1]+dp[v][j][1][0]+dp[v][j][1][1]))$

整理一下：

$dp[x][i+j][0][0]=\sum dp[x][i][0][0]*dp[v][j][0][1]$

$dp[x][i+j][1][0]=\sum dp[x][i][1][0]*(dp[v][j][0][0]+dp[v][j][0][1])$

$dp[x][i+j][0][1]=\sum (dp[x][i][0][1]*(dp[v][j][0][1]+dp[v][j][1][1])+dp[x][i][0][0]*dp[v][j][1][1])$

$dp[x][i+j][1][1]=\sum (dp[x][i][1][0]*(dp[v][j][1][0]+dp[v][j][1][1])+dp[x][i][1][1]*(dp[v][j][0][0]+dp[v][j][0][1]+dp[v][j][1][0]+dp[v][j][1][1]))$

不是很长对吧

小心：这题dp数组开long long是会MLE的，要中间运算过程中转long long然后再转回int

就差不多了

#include <cctype>
#include <cstdio>
#include <climits>
#include <algorithm>
#include <vector>

template <typename T> inline void read(T& t) {
    int f = 0, c = getchar(); t = 0;
    while (!isdigit(c)) f |= c == '-', c = getchar();
    while (isdigit(c)) t = t * 10 + c - 48, c = getchar();
    if (f) t = -t;
}
template <typename T> inline bool chkMin(T& x, const T& y) { return y < x ? (x = y, true) : false; }
template <typename T> inline bool chkMax(T& x, const T& y) { return x < y ? (x = y, true) : false; }
#ifdef WIN32
#define LLIO "%I64d"
#else
#define LLIO "%lld"
#endif	// WIN32 long long
#define rep(I, A, B) for (int I = (A); I <= (B); ++I)
#define dwn(I, A, B) for (int I = (A); I >= (B); --I)
#define erp(I, X) for (int I = head[X]; I; I = next[I])

const int maxn = 1e5 + 7;
const long long mod = 1e9 + 7;
std::vector<int> G[maxn];
int dp[maxn][107][2][2], tmp[107][2][2];
int size[maxn];
int n, K;

inline int add(int x, long long y) {
    if (y >= mod) y %= mod;
    for (x += y; x >= mod; x -= mod);
    return x;
}
inline void ae(int x, int y) {
    G[x].push_back(y);
    G[y].push_back(x);
}
void dfs(int x, int fa) {
    size[x] = dp[x][0][0][0] = dp[x][1][1][0] = 1;
    for (unsigned e = 0; e < G[x].size(); ++e) {
        int v = G[x][e];
        if (v != fa) {
            dfs(v, x);
            rep(i, 0, std::min(size[x], K)) {
                tmp[i][0][0] = dp[x][i][0][0]; dp[x][i][0][0] = 0;
                tmp[i][0][1] = dp[x][i][0][1]; dp[x][i][0][1] = 0;
                tmp[i][1][0] = dp[x][i][1][0]; dp[x][i][1][0] = 0;
                tmp[i][1][1] = dp[x][i][1][1]; dp[x][i][1][1] = 0;
            }
            rep(i, 0, std::min(size[x], K))
                rep(j, 0, std::min(size[v], K - i)) {
                    dp[x][i + j][0][0] = add(dp[x][i + j][0][0], 1ll * tmp[i][0][0] * dp[v][j][0][1]);

                    dp[x][i + j][0][1] = add(dp[x][i + j][0][1], 1ll * tmp[i][0][1] * (dp[v][j][0][1] + dp[v][j][1][1]));
                    dp[x][i + j][0][1] = add(dp[x][i + j][0][1], 1ll * tmp[i][0][0] * dp[v][j][1][1]);

                    dp[x][i + j][1][0] = add(dp[x][i + j][1][0], 1ll * tmp[i][1][0] * (dp[v][j][0][0] + dp[v][j][0][1]));

                    dp[x][i + j][1][1] = add(dp[x][i + j][1][1], 1ll * tmp[i][1][0] * (dp[v][j][1][0] + dp[v][j][1][1]));
                    dp[x][i + j][1][1] = add(dp[x][i + j][1][1], 1ll * tmp[i][1][1] * (1ll * dp[v][j][0][0] + dp[v][j][0][1] + 1ll * dp[v][j][1][0] + dp[v][j][1][1]));
                }
                size[x] += size[v];
        }
    }
}

int main() {
    read(n); read(K);
    rep(i, 1, n - 1) {
        int x, y;
        read(x); read(y); ae(x, y);
    }
    dfs(1, 0);
    printf("%d\n", (int)((dp[1][K][0][1] + dp[1][K][1][1]) % mod));
    return 0;
}