自动搬运

查看原文

来自洛谷，原作者为

	nekko **

搬运于2025-08-24 22:00:56，当前版本为作者最后更新于2018-09-07 18:59:02，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

同步于：我的博客

首先要解决一个问题，如何求一堆三角形的面积交？

首先$S=R^2$，求最终交出来的三角形的直角边长也行

设第$i$个三角形的左下角顶点坐标为$(x_i,y_i)$，边长为$r_i$，记$c_i=x_i+y_i+r_i$

则$R_{\cap}=\max(0,\min(c_i)-\max(x_i)-\max(y_i))$

既$S_{\cap}=R_{\cap}^2$

证明：

如果最终可以交出来三角形，那么无非也就如下几种情况（黑色为$c_i$最小的三角形，红色为交出的三角形）：

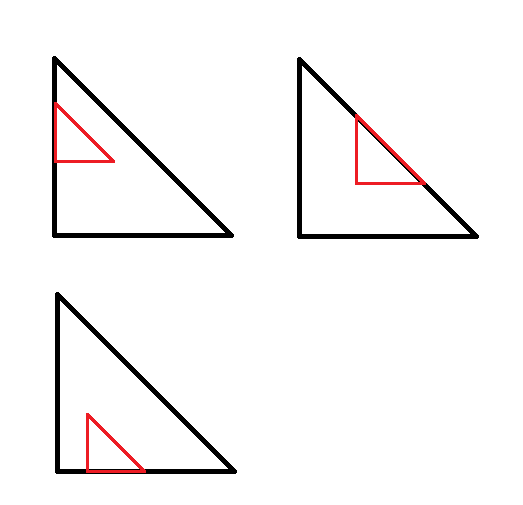
将变量设出来后显然得证

设$f(S)$表示选用集合$S$的三角形所交出来的三角形的面积

现在的目标是求$ans=\sum_{\emptyset \subsetneq S \subseteq U} f(S)g(| S |)$

也就是凑容斥系数

实际上$g(|S|)=(-1)^{|S|+1}2^{|S|-1}=(-2)^{|S|-1}$

证明：

对于一个交出来的三角形，设一共有$k$个三角形中包含这个三角形

即证：

$$\sum_{i=1}^{k}{k \choose i}(-1)^{i+1}2^{i-1}=[2 \nmid k] $$

也就是

$$\begin{aligned}\sum_{i=1}^{k}{k \choose i}(-1)^{i+1}2^{i-1}&=\sum_{i=1}^{k}{k \choose i}(-2)^{i-1} \\&=\frac{1}{-2}\sum_{i=1}^{k}{k \choose i}(-2)^{i} \\&=\frac{-{k \choose 0}(-2)^0+\sum_{i=0}^{k}{k \choose i}(-2)^{i}}{-2} \\&=\frac{-1+(-2+1)^{k}}{-2} \\&=\frac{1-(-1)^{k}}{2} \\ &=[2 \nmid k]\end{aligned} $$

于是就做完了

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
struct TRI { ll x, y, r, c; } tri[12];
ll ans; int n;
void dfs(int i, ll x, ll y, ll c, int sz, int sig) {
	if(x + y >= c) return ;
	if(i == n + 1) sz ? (ans += sig * (1ll << (sz - 1)) * (c - x - y) * (c - x - y)) : 0;
	else dfs(i + 1, x, y, c, sz, sig), dfs(i + 1, max(x, tri[i].x), max(y, tri[i].y), min(c, tri[i].c), sz + 1, -sig);
}
int main() {
	cin >> n;
	for(int i = 1 ; i <= n ; ++ i) cin >> tri[i].x >> tri[i].y >> tri[i].r, tri[i].c = tri[i].x + tri[i].y + tri[i].r;
	dfs(1, 0, 0, 1e18, 0, -1);
	printf("%.1lf\n", ans / 2.0);
}