1 条题解

  • 0
    @ 2025-8-24 22:00:48

    自动搬运

    查看原文

    来自洛谷，原作者为

    avatar xzyxzy
    被pku里高三的巨佬们虐惨了啊啊啊啊

    搬运于2025-08-24 22:00:48，当前版本为作者最后更新于2019-02-08 11:18:21，作者可能在搬运后再次修改，您可在原文处查看最新版

    自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

    以下是正文

    追求更佳阅读体验：BLOG。记得推荐&点赞哦！

    [ZJOI2018]保镖

    Tags：题解

    题意

    链接

    初始在平面上有一些点，九条可怜随机出现在一个矩形内的任意一点。若九条可怜出现在OO点，则平面上所有的点都从PiP_i移动到Pi′P'_i，使得Pi′P'_i在射线OPiOP_i上，且满足∣OPi∣∗∣OPi′∣=1|OP_i|*|OP'_i|=1。现在给定矩形范围，求这些点移动后所构成的凸包的期望点数。

    n≤2000,x,y≤105n\le 2000,x,y\le 10^5，精度要求绝对误差或相对误差不超过10−710^{-7}。

    题解

    前言

    神仙不可做题终于被杠下来了！撒花！

    不得不说九老师这个多合一是出的真的牛逼！（比lalaxu不知道高明到哪里去了）

    首先感谢Ez3real的代码框架（不过LOJ两人AC代码一样什么鬼）和yuhaoxiang的题解（这个网站很慢）。

    Part 1 前置知识：圆与矩形的面积交

    在计算几何基础里有。

    Part 2 前置知识：三维凸包

    在三维凸包里有。

    Part 3 前置知识：欧拉公式

    在Pick定理、欧拉公式和圆的反演里有。

    Part 4 前置知识：反演

    这道题显然是要求平面上的点关于OO的、以11为反演幂（反演半径）的反形的凸包期望点数。

    至于反演是什么可以看这个：Pick定理、欧拉公式和圆的反演

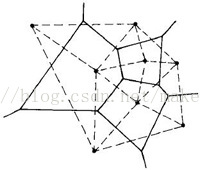
    Part 5 前置知识：Voronoi图

    又称泰森多边形。

    大概就是一个平面划分，平面上的每个点划分到离它最近的关键点上。

    Wiki有张十分形象的图

    Part 6 前置知识：Delaunay三角剖分

    三角剖分

    感性理解一下就是

    Delaunay三角剖分是一种有着优秀性质的三角剖分。

    定理：对于任何一种三角剖分，三角形个数和外围凸包点数之和为2n-2。

    这里凸包是严格凸的，也就是没有三点共线情况。

    考虑用欧拉公式证明：设凸包上的点数为kk，三角形个数为F−1F-1，则有

    $$V-E+F=n-((F-1)*3+k)/2+F=2$$凸包上的边算了一次，三角形上的边算了两次、 即$$k+F=2n-1,k+F-1=2n-2$$

    立体Delaunay三角剖分

    当然我们目前只考虑平面的Delaunay三角剖分，至于立体的可以看看这张图，本文不会涉及。

    （图片来源于网络）


    Delaunay三角剖分和泰森多边形

    Delaunay三角剖分和泰森多边形是对偶图。

    对偶图是什么呢，看下面的构造方法：

    泰森多边形的交点一般属于三个区域，将这三个区域的标志点连起来，就得到了一个原图的三角剖分。

    （图片来源于网络）

    上图中，实线是泰森多边形，虚线链接，得到标志点的一个Delaunay三角剖分。


    Delaunay三角剖分的性质

    由于其美妙的构造，可以得到一些美妙的性质：

    • 平面上的点集有且仅有唯一的Delaunay三角剖分（除出现四点共圆的情况，这时泰森多边形有顶点属于四个区域）。

    • 任意一个Delaunay三角形的外接圆不包含点集中的其他点。（称为Delaunay三角形的空圆性质）。

    • Delaunay三角剖分相比其他的三角剖分，所有三角形的最小角最大


    Delaunay三角剖分的构造

    以下内容摘自百度百科

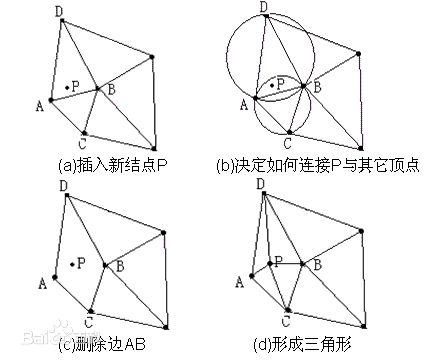
    Bowyer-Watson算法

    1. 构造超级三角形（类似半平面交中的超级平面）。

    2. 插入点PP，找到点PP的影响三角形（外接圆包括点PP的三角形），删除影响三角形的公共边，并把PP向这些影响到的点连边。

    3. 对原图进行优化

    4. 重复22直到所有点插入完毕

    步骤2图示：

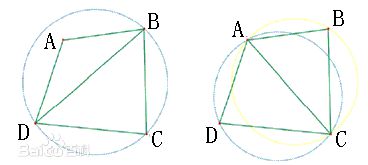
    步骤3图示：转变连接对角线的方式使其满足空圆性质

    和求三维凸包类似的复杂度分析，复杂度大概是O(n2)\cal O(n^2)

    Part 7 初步转化

    凸包点数，只能整体地去求，由于三角剖分的定理，我们可以转而求三角剖分的三角形个数。

    三角形个数是可以用期望算的。

    每一个Delaunay三角形对应一个外接圆，我们称为Delaunay圆。所以题目又转化为算Delaunay圆的期望个数。若Delaunay圆的期望个数为numnum，答案就是Ans=2n−2−numAns=2n-2-num。

    定义支配圆为包含点集中所有点的圆。Delaunay圆内不包含除Delaunay三角形三个顶点外的其他任何点，所以支配圆与Delaunay圆恰好相反。

    则以下结论成立

    • 对于Delaunay圆，若反演中心在圆内，其反形是支配圆；否则反形还是Delaunay圆。

    • 对于支配圆，若反演中心在圆内，其反形是Delaunay圆；否则反形还是支配圆。

    这题不用考虑反演中心在圆周上的情况（概率为0）

    这里有yuhaoxiang大佬做的一个Geogebra演示文件，我把两种情况截图下来是这样的：

    Delaunay圆，反演中心在圆内，反形是支配圆

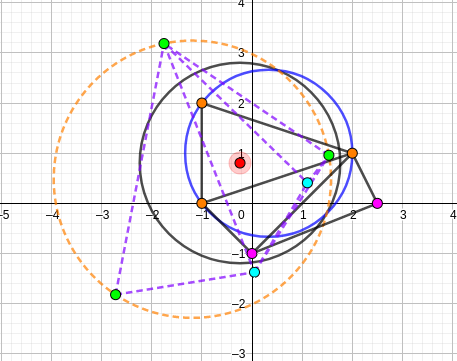
    Delaunay圆，反演中心在远外，反形还是Delaunay圆

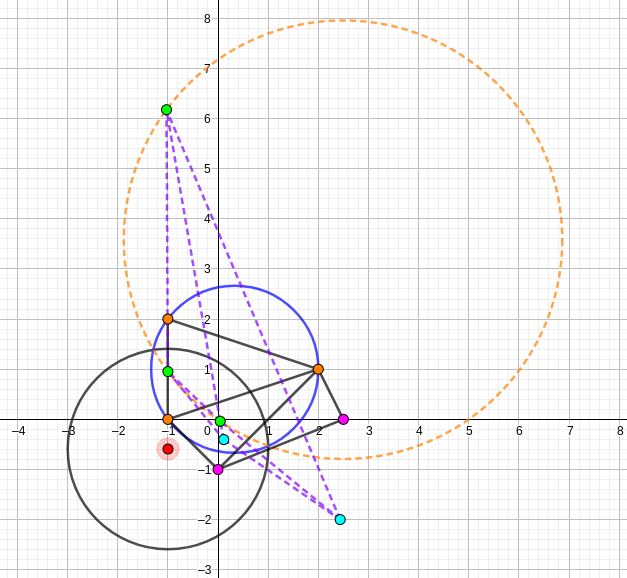
    题目转化为：求原图中Delaunay圆的个数×反演中心在圆内的概率+支配圆的个数×反演中心在圆外的概率

    若其期望为EE，则Ans=2n−2−Ans=2n-2-反形是Delaunay圆的概率=2+E=2+E

    （这句话看完Part8Part 8再回来看）对于这nn个点，每个点一定至少会是一个Delaunay圆对应的其中一个顶点，所以这nn个点每个点都会出现在凸包上，则凸包一共有2n−42n-4个面，所以Delaunay圆+支配圆=2n−4=2n-4。

    Part 8 进一步转化

    考虑圆的方程$$x^2+y^2+Dx+Ey+F=0$$若令z=x2+y2z=x^2+y^2，可以得到Dx+Ey+z+F=0Dx+Ey+z+F=0，这是空间坐标系中的一个平面方程

    z=x2+y2z=x^2+y^2长这样：

    例如圆(x−1)2+(y−1)2=1(x-1)^2+(y-1)^2=1可以表示为−2x−2y+z+1=0-2x-2y+z+1=0，长这样：

    自己做了一个动画：网址。

    那么如果一个点(x,y)(x,y)在圆上，则(x,y,x2+y2)(x,y,x^2+y^2)在该圆对应的平面上

    同理，在圆外或圆内，对应着在平面的一侧。具体来说，在其平面上面表示在圆外，在平面下面表示在圆内。

    于是，把所有点映射到三维坐标系中，求凸包，下凸面对应Delaunay圆，上凸面对应支配圆。

    Part 9 实现过程

    首先读入所有的点并进行随机微小扰动，使得不存在多点共圆以及最后求出三维凸包中不存在与$z

    $轴平行的凸面。

    然后求解三维凸包，这里采用的是增量法。

    对于每个凸面，得到对应的三个点、求出其外接圆。

    • 如果其为上凸面，则其为支配圆，只有在反演中心在圆外，贡献答案

    • 如果其为下凸面，则其为Delaunay圆，只有反演中心在圆内，贡献答案

    那么就是算给定矩形和圆形的面积交，这个在前置知识Part1Part 1里啦

    Part 10 总结&代码

    写了一年终于写完了！

    完结撒花！！

    这题考场上一定要果断丢，没有部分分。

    这题出得很好，考察知识点全面。很巧妙的地方是：巧妙地把圆转化成三维空间的平面，从而把平面问题转化为三维凸包问题。巧妙地运用三角剖分，把求凸包顶点期望个数变为求圆的期望个数。

    不得不说，orz jiry!!!

    Code

    #include<iostream>
#include<cmath>
#define db __float128
#define orzjiry_2 19491001
using namespace std;
const db eps=1e-10;
db Rand() {return 1.0*rand()/RAND_MAX;}
int sign(db x) {return x<-eps?-1:(x>eps);}
struct v2
{
	db x,y;
	v2 operator + (v2 a) {return (v2){x+a.x,y+a.y};}
	v2 operator - (v2 a) {return (v2){x-a.x,y-a.y};}
	v2 operator / (db t) {return (v2){x/t,y/t};}
	v2 operator ^ (db t) {return (v2){x*t,y*t};}
	db operator * (v2 a) {return x*a.y-y*a.x;}
	db operator & (v2 a) {return x*a.x+y*a.y;}
	db dis() {return sqrt((double)(x*x+y*y));}
	db dis2() {return x*x+y*y;}
	void rot() {db t=x;x=-y;y=t;}
}jir[4];
struct v3
{
	db x,y,z;
	v3 operator + (v3 a) {return (v3){x+a.x,y+a.y,z+a.z};}
	v3 operator - (v3 a) {return (v3){x-a.x,y-a.y,z-a.z};}
	v3 operator * (v3 a) {return (v3){y*a.z-z*a.y,z*a.x-x*a.z,x*a.y-y*a.x};}
	db operator & (v3 a) {return x*a.x+y*a.y+z*a.z;}
	void shake() {x+=Rand()*1e-10,y+=Rand()*1e-10,z+=Rand()*1e-10;}
}P[2100];
struct Face
{
	int v[3];
	v3 Normal() {return (P[v[1]]-P[v[0]])*(P[v[2]]-P[v[0]]);}
}F[8100],C[8100];
int n,cnt;

namespace TAT2D
{
	v2 Cross(v2 a1,v2 a2,v2 b1,v2 b2)
	{
		v2 a=a2-a1,b=b2-b1,c=b1-a1;
		db t=(b*c)/(b*a);
		return a1+(a^t);
	}
	int cmp(db a,db b) {return sign(a-b);}
	db rad(v2 p1,v2 p2) {return atan2(double(p1*p2),double(p1&p2));}
	db Calc(db r,v2 p1,v2 p2)
	{
		v2 e=(p1-p2)/(p1-p2).dis(),e1=e;e.rot();
		v2 mid=Cross(p1,p2,(v2){0,0},e),d1=mid;
		if(d1.dis()>r) return r*r*rad(p1,p2)/2;
		db d=sqrt(double(r*r-d1.dis2()));
		v2 w1=mid+(e1^d),w2=mid-(e1^d);
		int b1=cmp(p1.dis2(),r*r)==1,b2=cmp(p2.dis2(),r*r)==1;
		if(b1&&b2)
		{
			if(sign((p1-w1)&(p2-w1))<=0)
				return r*r*(rad(p1,w1)+rad(w2,p2))/2+(w1*w2)/2;
			else return r*r*rad(p1,p2)/2;
		}
		if(b1) return (r*r*rad(p1,w1)+w1*p2)/2;
		if(b2) return (p1*w2+r*r*rad(w2,p2))/2;
		return p1*p2/2;
	}
	db intersect(v2 O,db r)
	{
		db res=0;
		for(int i=0;i<4;i++)
			res+=Calc(r,jir[i]-O,jir[(i+1)%4]-O);
		return res;
	}
}

namespace TAT3D
{
	bool vis[2100][2100];
	int see(Face a,v3 b) {return ((b-P[a.v[0]])&a.Normal())>0;}
	void Convex()
	{
		for(int i=0;i<n;i++) P[i].shake();
		int cc=-1;cnt=-1;
		F[++cnt]=(Face){0,1,2};
		F[++cnt]=(Face){2,1,0};
		for(int i=3;i<n;i++)
		{
			for(int j=0,v;j<=cnt;j++)
			{
				if(!(v=see(F[j],P[i]))) C[++cc]=F[j];
				for(int k=0;k<3;k++) vis[F[j].v[k]][F[j].v[(k+1)%3]]=v;
			}
			for(int j=0;j<=cnt;j++)
				for(int k=0;k<3;k++)
				{
					int x=F[j].v[k],y=F[j].v[(k+1)%3];
					if(vis[x][y]&&!vis[y][x]) C[++cc]=(Face){x,y,i};
				}
			for(int j=0;j<=cc;j++) F[j]=C[j];
			cnt=cc;cc=-1;
		}
	}
}

int main()
{
	//Part 1 输入以及初步转化
	srand(orzjiry_2);
	double xx,yy;
	cin>>n>>xx>>yy;jir[0]=(v2){xx,yy};
	cin>>   xx>>yy;jir[2]=(v2){xx,yy};
	jir[1]=(v2){jir[2].x,jir[0].y};
	jir[3]=(v2){jir[0].x,jir[2].y};
	db S=(jir[2].x-jir[0].x)*(jir[2].y-jir[0].y),Ans=0;
	for(int i=0;i<n;i++)
	{
		double x,y;cin>>x>>y;
		P[i]=(v3){x,y,x*x+y*y};
	}
	//Part 2 计算三维凸包并求出反演后支配圆的期望数量
	TAT3D::Convex();
	for(int i=0;i<=cnt;i++)
	{
		v3 o=F[i].Normal();
		v2 a1=(v2){P[F[i].v[0]].x,P[F[i].v[0]].y};
		v2 a2=(v2){P[F[i].v[1]].x,P[F[i].v[1]].y};
		v2 c=(a1+a2)/2.0,d=a2-a1;d.rot();
		a1=c;a2=c+d;
		v2 b1=(v2){P[F[i].v[1]].x,P[F[i].v[1]].y};
		v2 b2=(v2){P[F[i].v[2]].x,P[F[i].v[2]].y};
		c=(b1+b2)/2.0,d=b2-b1;d.rot();
		b1=c;b2=c+d;
		v2 O=TAT2D::Cross(a1,a2,b1,b2);
		d=(v2){P[F[i].v[0]].x,P[F[i].v[0]].y};
		db r=(O-d).dis();
		if(o.z>0) Ans+=S-TAT2D::intersect(O,r);
		else Ans+=TAT2D::intersect(O,r);
	}
	printf("%.11f\n",(double)(Ans/S+2));
}
    • 1

    [ZJOI2018] 保镖

    信息

    ID
    3485
    时间
    4000ms
    内存
    500MiB
    难度
    7
    标签
    递交数
    0
    已通过
    0
    上传者
    1. 关于
    2. 联系我们
    3. 隐私
    4. 服务条款
    5. Language
    6. 主题
    3. Worker 0, 35ms