1 条题解
-
0
自动搬运
来自洛谷,原作者为

inc1ude_c
兴尽悲来,喜多郁代搬运于
2025-08-24 22:00:46,当前版本为作者最后更新于2024-04-12 19:18:31,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
第一篇黑题题解,哪里讲的有错希望能指出。
Part -1
传说中搜不到题解的题(之一)。
但是科学上网后还是搜到了一篇 VFleaking 的题解,结果里面的图挂了看着相当吃力……搞了几天才做出来。
前置知识倒也不是太多,会使用并查集求出桥与边双连通分量就可以了。
请留下充足的时间与耐心来看这篇题解。
Part 0
首先有两个定义:对于一层图的边我们叫横边,对于连接相邻两层图的边我们叫竖边。
我们需要清楚这条事实:对于同一条边,要么一直是桥,要么一直不是桥,要么只在前若干层是桥。
这样我们就可以很方便地算贡献了:
-
对于一条边,它一直是桥,则贡献为 。
-
对于一条边,它只在前 层是桥,则贡献为 。其中 。
Part 1
我们先搞定第一层。
我们要求的东西是:
- 两个并查集 和 ,分别管理第一层所有连通分量,和第一层所有边双连通分量。
这个可以在第一层(不包括竖边)上 DFS 一遍求出。
但我们还是要考虑竖边,于是我们考虑扫一遍竖边,求出这些东西:
-
,表示第一层的以 为根的连通块上以 为左端点的竖边是哪一条?
-
,表示第 条横边是不是桥。
-
,表示第 条竖边是不是桥。
这些东西可以揉在一起做,算法如下:
初始时 与 皆为真。
遍历所有竖边,当前遍历的竖边为 ,这时看 的左端点(简称 )是否有没有被访问:
-
若没有,则 是一个连通块的根。对其 DFS,并且 就是 。
-
若有,则找到 所在连通块的根,把 到这个根的 的左端点路径上的边双都合并一下。
rep(i,1,m2){ if(!vis[e2[i].u])dfs(e2[i].u,0),cctop[e2[i].u]=i; else{ int j=ufs1.find(e2[i].u);mpath(e2[i].u,e2[cctop[j]].u); bri2[i]=bri2[cctop[j]]=0; } }mpath是将两点路径上的边双都合并并返回上面所有桥的 之和。可以在题解的在最后看到。我们为什么要求出这些东西?为了求出第一层的每个连通分量通过竖边与哪些边双连通分量直接相连。
Part 2
在这之前先定义一些东西吧:
- 只考虑前 行,若第 行 之间有路,则 属于一个奇葩连通分量。
- 只考虑前 行,若第 行 之间有不经过桥的路,则 属于一个奇葩边双连通分量。
- 对于一个奇葩连通分量,如果它往下只对 个奇葩边双连通分量有连边,则它就是没存在感的。
这些定义都是沿用的 VFleaking 题解中的定义。orz VFleaking。
我们发现最开始 和 已经求出对于前 行的奇葩连通分量与奇葩边双连通分量。
考虑从第 行转移到第 行,奇葩连通分量与奇葩边双连通分量(即那两个并查集)有哪些变化。显然我们要对一些竖边分类讨论。
情况一:某第 行奇葩连通分量和某第 行奇葩边双连通分量间连有很多条边。
只需要保留一条就可以了,我们关心的是每个奇葩连通分量与哪些奇葩边双连通分量直接相连。
情况二:某第 行奇葩连通分量只和某第 行奇葩边双连通分量有边。
这就是我们上面定义的“没存在感的奇葩连通分量”。这里解释一下为什么是“没存在感的”:只与一个边双有边意味着不会有环,就不会发生合并,没有合并就不会对第 层有任何影响。
当然你可能有我最开始的这样的疑问:如果它们只有一条边相连,那这条边不就是桥吗?那能叫“没有任何影响”?注意我们是关心边在哪层就不是桥了,这点在 Part 0 就提到过。
情况三:某第 行奇葩连通分量和第 行某两个处于同一奇葩连通分量的奇葩边双连通分量有边。
合并边双,具体看图:
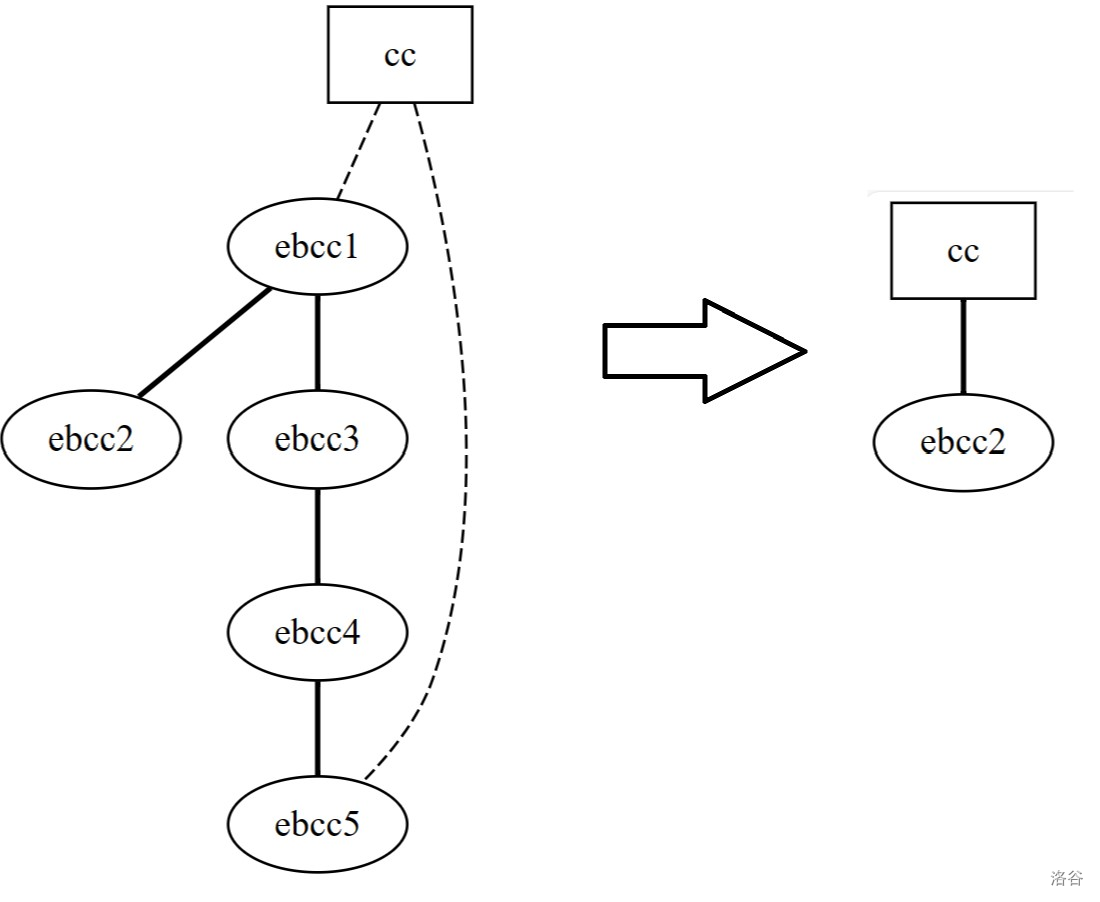
粗边指的是桥。
我们就是把两个路径上的边双合并,然后这些被合并的桥都不再是桥了,于是我们结算贡献,这也就是为什么
mpath要返回桥的权值和。情况四:某第 行奇葩连通分量和第 行某两个奇葩连通分量有边。
的改动:合并这两个奇葩连通分量。
的改动:我们把连通分量看成由边双组成的树:
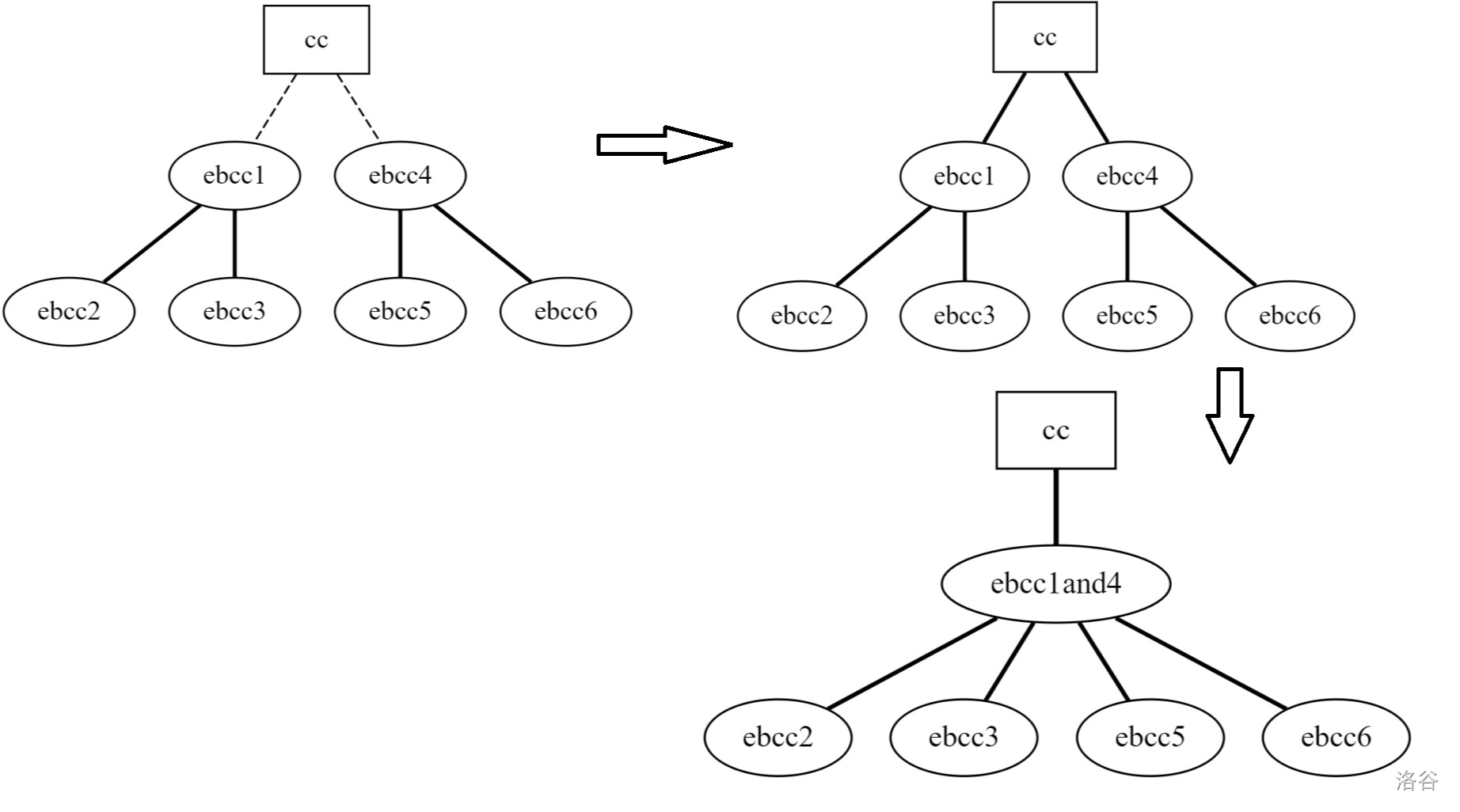
我们把这两个奇葩连通分量的两个根奇葩边双连通分量合并即可。
这样,我们不停对第 行的奇葩连通分量进行这样的合并,最终都会变成没存在感的。
但是算法什么时候结束呢???
Part 3
我们在从 转移到 时,记录第 行中有存在感的奇葩连通分量,存在数组 ,这样下次转移就遍历这些奇葩连通分量。
然后如果我们在上面的记录中,没有有存在感的奇葩连通分量,那我们就可以停止算法了,因为我们下一次从 转移到 时,没有奇葩连通分量可以遍历了……
我们动态维护 ,但我们发现我们需要在一个较优的复杂度内求出第 行每个奇葩连通分量向下连的边。
现在我们定义一个新东西:
- ,表示下一层唯一一个和这一层的奇葩连通分量 有连边的奇葩边双连通分量是啥。
这个东西显然在没存在感的奇葩连通分量上才有值。
而因为第 层被扫了后每个奇葩连通分量都没有存在感,所以其 都有值。
我们下画图,这里奇葩边双连通分量就用点表示吧。
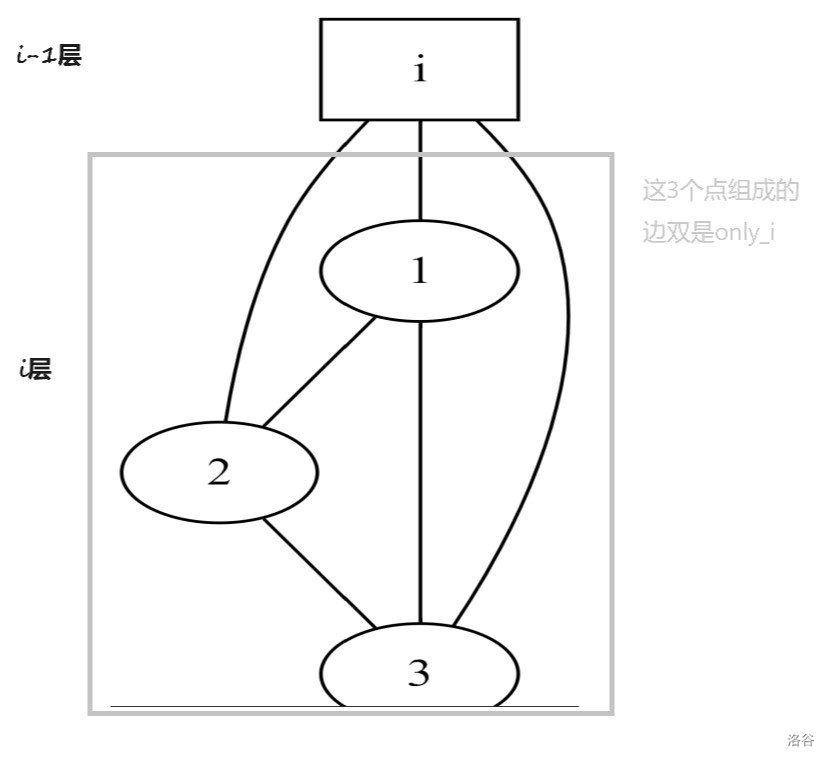
注意在第 层也有节点 ,而它在 层属于的奇葩连通分量也必有 ,设这个 为 。
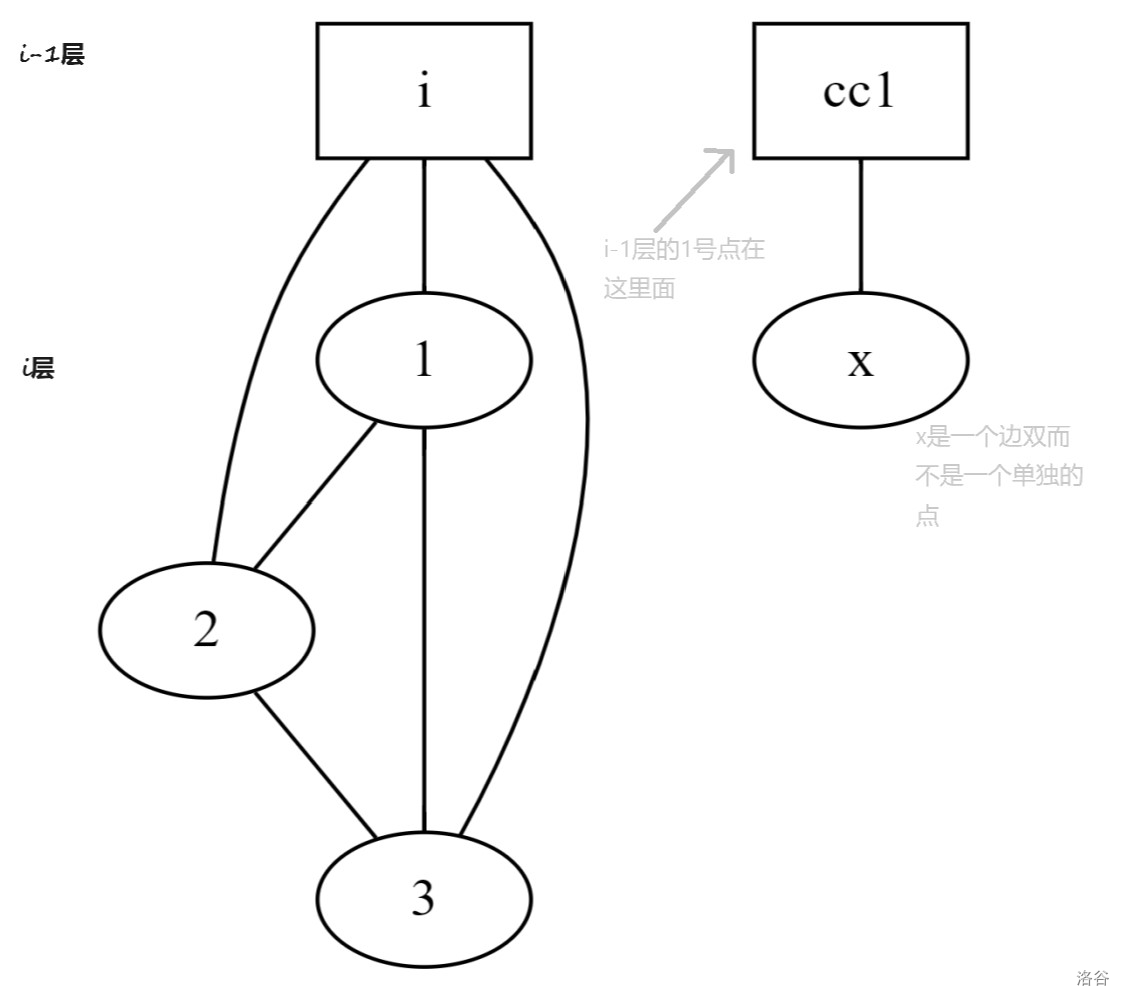
那么根据竖边的复制原理, 层的 所在的奇葩连通分量也应该往 层的边双 连边。
那我们不就求出 层要向下连的边了吗?
Part 4
时间复杂度?按照 VFleaking 的说法,每条边被缩起来后再也不会被访问,而且缩边不会超过 次,所以复杂度为 或者后面不是 而是反阿克曼函数。
不过 VFleaking 说他不确定,所以我也不敢直接下结论,但实测程序跑的飞快。
-
- 1
信息
- ID
- 3476
- 时间
- 3000ms
- 内存
- 125MiB
- 难度
- 7
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
