自动搬运

查看原文

来自洛谷，原作者为

	45dino 不要停下来啊>_<

搬运于2025-08-24 22:00:46，当前版本为作者最后更新于2022-09-21 19:21:52，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

难过。

由于走不同的路有不同的速度，最短路径的形态是一个变化很大的东西。直接构造或贪心大概率是不对的，但是注意到如果把最优情况画出来的话，应该也是一条折线（称为“最优折线”），如果把原平面转化成一个无向图，最优折线就是一条从起点到终点的路径。因此可以考虑建一个图然后跑最短路。

一开始觉得最优折线每一段起点终点都应该是原本的折线端点，因此直接用原本折线端点为顶点，建 $n^2$ 条边。但这样是错误的。反例显而易见：

如图，起点是 $A$，终点是 $C$，最优的路径大概长这样（假设 $va=2,vb=1$）

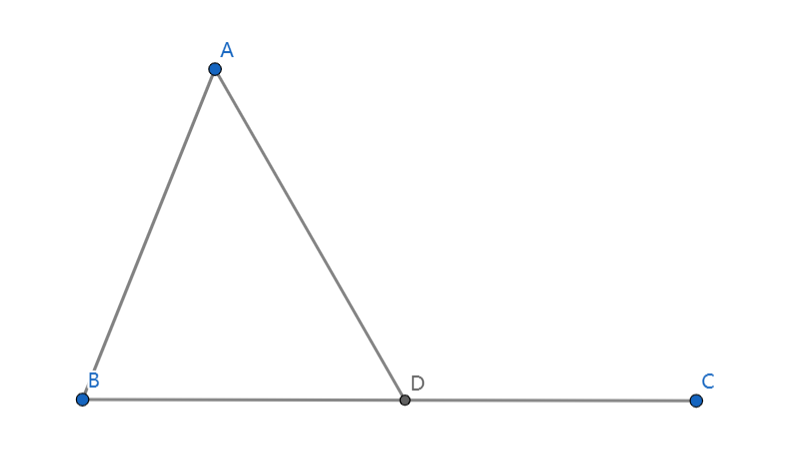
如你所见，经过了一个中转点 $D$，但是 $D$ 并不是端点。

可以发现，虽然最优折线的端点不一定在原本折线的端点上，但是一定在原本折线上。（因为在沙地里转变方向是不优的）

折线的端点只有 $n$ 个，但是折线上的点有无限个，这种情况下要考虑哪些点是有意义的，只将这些有意义的点加入最后的拓扑图里。

可以枚举边，对于每一条边，求出上面哪些点是有意义的。对于原本折线上的一条边 $BC$ 上的点 $P$ 是有意义的当且仅当存在一个端点 $A$，使得 $\frac {AP} {vb}+\frac {BP} {va}$ 是所有 $BC$ 上的点中最小的；或者使得 $\frac {AP} {vb}+\frac {CP} {va}$ 是所有 $BC$ 上的点中最小的。如果枚举 $A,B,C$，符合条件的 $P$ 的位置是能被确定的。大多数题解都是用一些怪异的公式进行推导，这里提供一个初等数学的做法。

其实这是一个著名的初中数学模型——胡不归问题。

给定 $A,B,C$ 三点，试在直线 $BC$ 上找一点 $P$，使得 $AP+\frac {CP} k$ 最小，其中 $0<k<1$。

构造 $\angle BCB'$，使得 $\cos \angle BCB'=\frac 1 k$，作 $AD\perp B'C$，则 $AD$ 与 $BC$ 交点 $P$ 即为所求。

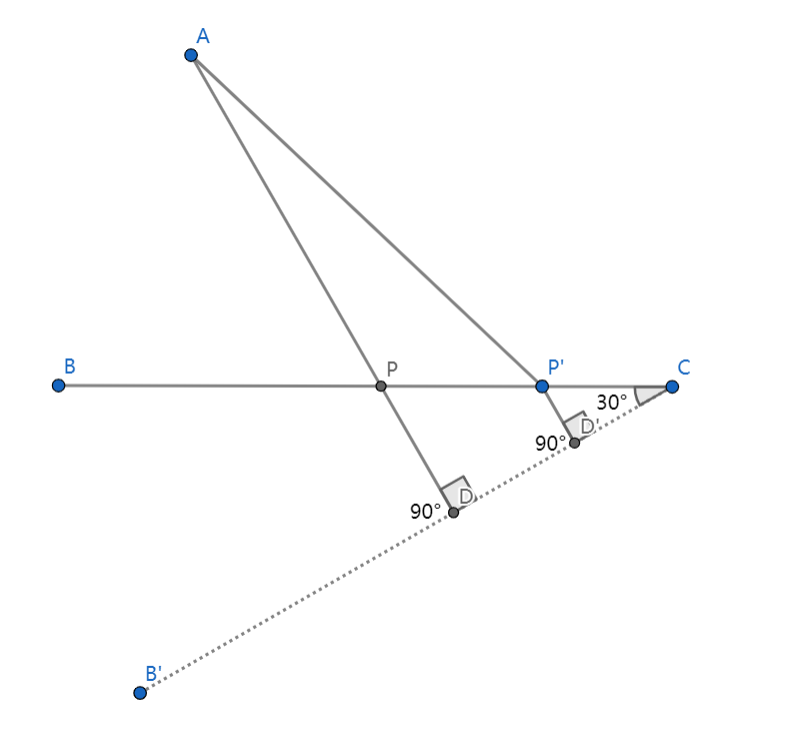
证明不难：由构造过程可得 $DP=\frac {CP} k$，因此 $AP+\frac {CP} k=DP+AP=AD$。如果取 $BC$ 上的另一个不同于 $P$ 的点 $P'$，作 $P'D'\perp B'C$，则有 $AP'+\frac {CP'} k=D'P'+AP'>AD$。

在原问题中，$k=\frac {vb} {va}$，可以根据 $BC$ 求出 $AD$，进而确定交点 $P$，只需要判断 $P$ 是否在线段 $BC$ 上即可。这样就可以对于每一条边，求出该边上所有有意义的点。显然点数和边数都是 $\mathcal O(n^2)$ 的。

这一题放在 WC，不仅可以体现国集选手的思维能力和计算几何代码能力，更多的是对 whk 的考察（？）

后记：Geogebra 是真的香。