1 条题解
-
0
自动搬运
来自洛谷,原作者为

disangan233
ディストピア搬运于
2025-08-24 22:00:45,当前版本为作者最后更新于2019-02-27 22:35:13,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
前言
- 这是本蒟蒻的第一篇黑题题解,有误请轻喷。
- 更良好的观看体验:disangan233の博客
- PS:这题本蒟蒻因为某个数组连续开小找了两天两夜。
- 请勿抄袭代码。
(反正你代码又交不过) - 于 2020/10/7修订。
题意简述
- 给你坐标系上 个点 的坐标,让你求出新建 个节点 (可与已存在点重合)后,求 到 的最小费用最大流,并输出方案。
具体实现
首先,将题目仔细分析后,得出这样一个结论:
设新节点为 ,为了满足最优解,必定满足:
$$x_c \in \{ x_i|i \in [1,n]\},y_c \in \{ y_i|i \in [1,n]\} $$所以我们把原题就可以拆成横纵坐标来做。
输入1
显然这就是一个带权中位数,不懂的可以去看一维邮局问题。
可以将题意转换为给你 , 为 到 的距离,求
$$\min \left\{ \sum_{j=1}^{n} w_j \times d(i,j)| i\in [1,n] \right\} $$先假设 不存在,那么题目就让你求
$$\min \left\{ \sum_{j=1}^{n} d(i,j)| i\in [1,n] \right\} $$显然可以将 和 分别排序,求出中位数后枚举即可。
那么带权值的中位数即可在普通中位数的前提下,将 的个数修改为 即可。
上个图吧:
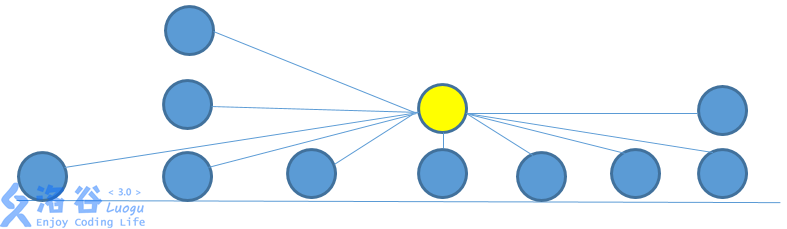
输入 2-10
首先先考虑跑最小费用最大流,发现 不好实现,于是考虑转换模型。
以 建立新节点,并将 拆成 个点 ,表示状态 建在上。
对于每一个 ,向 建一条流量为 的双向边,向 建一条流量为 的双向边。然后将源点向 , 向汇点,建一条流量为 的边。
为将 , 排序后, 建在 时的 和 。
这时将对于横纵坐标不同的 建图跑两次最小割,答案即为两次最小割之和。
上个图(黄边是双向边,画错了):
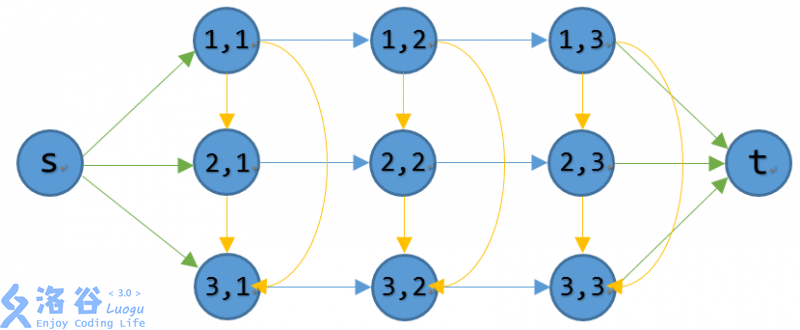
图中 ,绿色为 ,蓝色为 ,橙色为 。
输出方案
显然,在跑完最小割后的残流网络中,横向割边的出点即为答案所在的横(或纵)坐标。
这时候对于 ,,正反跑两次 dfs,将必定割边存入 即可。
但是这样你发现输入 7 会过不了!冷静分析后发现,必定割边的数量有可能小于 !
于是在疯狂的尝试后,你发现了所有的可能割边均可为答案,只跑源点即可。
正确性证明
献上这个熟悉的图:
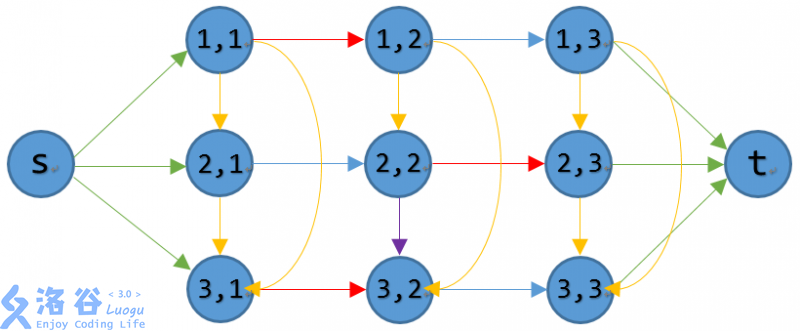
我们令红色边为影响方案决策的满流边,此时的最小割集中,为了割掉 和 ,我们发现紫色边也应该跟着一起满流,就满足了跑 的性质。
所以在 , 可重复的条件下,此建图方法正确。
温馨提示
你指望你的网络流能 1s 跑过 的数据?
醒醒!这是提交答案题!
源代码
远古码风,有空再改。
#include<bits/stdc++.h> using namespace std; #define re register int #define ll long long #define ak * #define fp(x,y) for(re i=1;i<=x;i++) for(re j=1;j<=y;j++) #define inf 1e18 int bj,tot,cnt=1,n,m,k,s,t,h[100005],dis[100005],l,r,q[100005],tt[2],wtf=233; int cur[100005],ansx[100005],ansy[100005],vis[100005]; ll w[100005],nx[100005],ny[100005],gx[305][305],gy[305][305],a[305][305],b[305][305],ans; struct did{ int u,next,to; ll f; }e[2000005]; struct node{ ll pos,val; bool operator <(node a) const {return pos<a.pos;} }x[100005],y[100005]; char qwq,mp; inline ll id(re x,re y) {return (x-1)*(n+1)+y;} inline ll read() { ll cz=0,ioi=1;qwq=getchar(); while(qwq<'0'||qwq>'9') ioi=qwq=='-'?~ioi+1:1,qwq=getchar(); while(qwq>='0'&&qwq<='9') cz=(cz<<3)+(cz<<1)+(qwq^48),qwq=getchar(); return cz ak ioi; } inline void add(re x,re y,ll z) { e[++cnt]=(did){x,h[x],y,z},h[x]=cnt; e[++cnt]=(did){x,h[y],x,0},h[y]=cnt; } inline int bfs(re u) { memset(dis,-1,sizeof(dis));dis[u]=0; l=r=0;q[++r]=u; while(l<r) { re i=q[++l]; if(i==t) return 1; for(re j=h[i],k;k=e[j].to,j;j=e[j].next) if(dis[k]<0&&e[j].f) dis[k]=dis[i]+1,q[++r]=k; } return 0; } inline ll dfs(re u,ll maxf) { ll res=0; if(u==t||maxf==0) return maxf; for(re &i=cur[u],v;v=e[i].to,i;i=e[i].next) if(e[i].f&&dis[v]==dis[u]+1) { ll delta=dfs(v,min(maxf,e[i].f)); e[i].f-=delta;e[i^1].f+=delta; res+=delta;maxf-=delta; if (!maxf) return res; } if (maxf!=res) dis[u]=-2; return res; } inline ll dinic() { ll ans=0; while(bfs(s)) { for(re i=s;i<=t;i++) cur[i]=h[i]; ans+=dfs(s,inf); } return ans; } inline ll calc(re a,re b) { return abs(nx[a]-nx[b])+abs(ny[a]-ny[b]); } void find(re u,re k) { vis[u]=k;tt[k]++; for(re i=h[u],v;v=e[i].to,i;i=e[i].next) if(e[i].f&&!vis[v]) find(v,k); } int main() { freopen("locate9.in","r",stdin); freopen("data.out","w",stdout); n=read(),m=read();s=0,t=m*(n+1)+1; for(re i=1;i<=n;i++) x[i].pos=nx[i]=read(),y[i].pos=ny[i]=read(); if(m==1) { ll res=0,xx,yy,sum=0,pre=0; for(re i=1;i<=n;i++) sum+=(x[i].val=y[i].val=w[i]=read()); sum=(sum&1)?sum/2+1:sum/2; sort(x+1,x+n+1);sort(y+1,y+n+1); for(re i=1;i<=n;i++) { if(pre+x[i].val>=sum) {xx=x[i].pos;break;} pre+=x[i].val; } pre=0; for(re i=1;i<=n;i++) { if(pre+y[i].val>=sum) {yy=y[i].pos;break;} pre+=y[i].val; } for(re i=1;i<=n;i++) res+=w[i]*(abs(xx-nx[i])+abs(yy-ny[i])); printf("%lld\n%lld %lld\n",res,xx,yy); return 0; } sort(nx+1,nx+n+1);sort(ny+1,ny+n+1); fp(n,m) a[i][j]=read(); for(re i=1;i<m;i++) for(re j=i+1;j<=m;j++) b[i][j]=b[j][i]=read(); fp(m,n) for(re k=1;k<=n;k++) { gx[i][j]+=abs(nx[j]-x[k].pos)*a[k][i]; gy[i][j]+=abs(ny[j]-y[k].pos)*a[k][i]; } for(re i=1;i<=m;i++) { for(re j=1;j<=n;j++) add(id(i,j),id(i,j+1),gx[i][j]); add(s,id(i,1),inf),add(id(i,n+1),t,inf); } for(re i=1;i<m;i++) for(re j=i+1;j<=m;j++) for(re k=2;k<=n;k++) { ll now=b[i][j]*(nx[k]-nx[k-1]); add(id(i,k),id(j,k),now);e[cnt].f=now; } ans+=dinic();find(s,1); fp(m,n) for(re k=h[id(i,j)];k;k=e[k].next) if(!e[k].f&&vis[id(i,j)]&&!vis[id(i,j+1)]&&e[k].to==id(i,j+1)) ansx[++ansx[0]]=nx[j]; cnt=1;memset(h,0,sizeof(h));s=0;t=m*(n+1)+1; for(re i=1;i<=m;i++) { for(re j=1;j<=n;j++) add(id(i,j),id(i,j+1),gy[i][j]); add(s,id(i,1),inf),add(id(i,n+1),t,inf); } for(re i=1;i<m;i++) for(re j=i+1;j<=m;j++) for(re k=2;k<=n;k++) { ll now=b[i][j]*(ny[k]-ny[k-1]); add(id(i,k),id(j,k),now);e[cnt].f=now; } ans+=dinic();memset(vis,0,sizeof(vis));find(s,1); fp(m,n) for(re k=h[id(i,j)];k;k=e[k].next) if(!e[k].f&&vis[id(i,j)]&&!vis[id(i,j+1)]&&e[k].to==id(i,j+1)) ansy[++ansy[0]]=ny[j]; printf("%lld\n",ans); for(re i=1;i<=m;i++) printf("%d %d\n",ansx[i],ansy[i]); return 0; }
- 1
信息
- ID
- 3473
- 时间
- 1000ms
- 内存
- 125MiB
- 难度
- 7
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
