自动搬运

查看原文

来自洛谷，原作者为

	SkqLiiiao **

搬运于2025-08-24 22:00:41，当前版本为作者最后更新于2018-05-18 12:02:33，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

[BJWC2018]【最小费用最大流】 kakuro

题意

kakuro是一个神奇的数独游戏，大致规则如下：

• $N\times M$ 的网格图中，由一些格子为空格需要填数，一些格子填线索，一些格子什么都不填
• 线索有两个方向，分别为右和下，线索的值表示该方向连续空格所填数之和
• 对于任意一个空格，其左边与上边的一定存在一个格子为线
• 参考下图

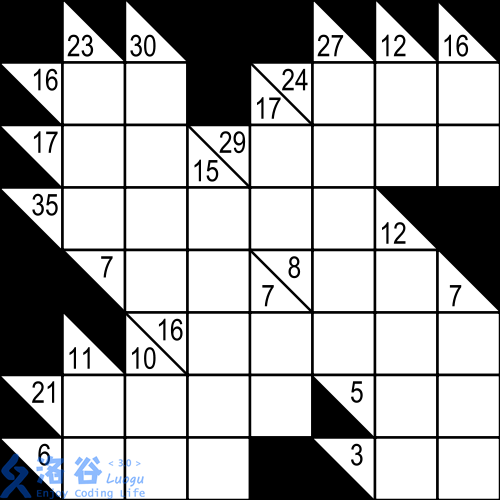
游戏规则：

• 空格中填入正整数。

• 被斜线分开的方格中，右上角的数字等于其右侧邻接之连续方格中数字之和，左下角的数字等于其下方邻接之连续方格中数字之和。

Apia 给了Rimbaud 一个Kakuro 谜题。心不灵手不巧的Rimbaud 根本不会做Kakuro，所以只在空格里面填上了一些随机的数字，称这个为一个局面，即包含了谜题一开始给出的线索和后面填入的数字。

现在Rimbaud 希望能修改这个局面使得她的答案是一个合法解。这个局面中有些数字(包括一开始的给出线索和后面填入的数字) 是可以修改的。每个数字都有个特定的代价，将这个数字加 $1$ 或者减 $1$ 都得付出这个数字对应的代价。注意对于一组合法解，必须满足游戏规则，也就是空格中填的数字必须是正整数并且满足和的条件，但是不要求不重复。

Rimbaud 希望用最少的代价让这个局面变得合法，如果不可能那么输出-1 。

数据范围

对于$100\%$ 的数据，保证$3 \leq n,m \leq 30$，保证初始局面中的每个数字不超过 $10^6$ ，保证每个数字的代价不超过 $10^6$ 。

题解

致谢

感谢AloNE的讲解。

正题

一个思路就是先做出一个合法解，然后再去修改权值以减少总花费。

那么最简单的合法解，就是每个空格都填 $1$ ，线索填对应格子的个数。

如此保证了每个空格都是正整数，这是一个最小解。

记当前花费为 $Ans$ 。

记某个格子现在的值为 $A(x,y)$ ，原来的值为 $O(x,y)$ ，修改 $1$ 的价格为 $C(x,y)$ 。

那么每个空格和线索只能往大修改，那么有两种情况。

• $A(x,y) \leq O(x,y)$ ，那么当 $A(x,y)$ 最初变大直到 $O(x,y)$ 时，相当于对最开始的修改进行反悔，也就是说花费 $-C(x,y)$；当然对于超出 $O(x,y)$ 的部分继续花费 $C(x,y)$ 。
• $A(x,y) \geq O(x,y)$ ，那么修改继续增加花费 $C(x,y)$ 。

转化成网络流问题，将这些关系抽象成如下的边：

• 发现对于修改一个空格会对其左边和上边的两个线索产生影响，约束方法很简单，就是流量从其上面的线索流入，从其左边的线索流出，那么保证所有增加的流量都是合法的；也就是说空格本质就是一条连接横向和竖向线索的边；

• 根据上面的建模方法，$S$ 连接所有竖向线索，费用为 $C(x,y)$ ，流量不限；

• 所有横向线索连接 $T$ ，费用为 $C(x,y)$ ，流量不限；

• 对于所有空格，如果 $A(x,y) \leq O(x,y)$ ，连接费用为 $-C(x,y)$ 流量为 $O(x,y) - A(x,y)$ ，意为对最初的修改进行反悔；（对应的两个线索之间连边）

• 对于所有空格，连接费用为 $C(x,y)$ ，流量不限的边，因为每个格子都可以无限增大。

跑最小费用可行流，当前费用 $Cost \geq 0$ 时结束。

得到最小费用 $C$ ，那么最终结果 $Ans + C$ 。

那么如何判断无解的情况？

无解也就是说修改了不能修改的边。

那么将不能修改的边的费用置为 $INF$ ，跑完最小费用可行流之后检查残余网络是否存在费用为 $INF$ 的反向边流量不为 $0$ 或者费用为 $-INF$ 的边流量不为 $0$ 。

如果出现这种情况，说明了必须修改不能修改的格子权值以满足流量平衡，输出 -1 即可。

参考代码

// Copyright 2018, Skqliao
#include <bits/stdc++.h>

#define rg register
#define rep(i, l, r) for (rg int i = (l), _##i##_ = (r); i < _##i##_; ++i)
#define rof(i, l, r) for (rg int i = (l) - 1, _##i##_ = (r); i >= _##i##_; --i)
#define ALL(x) (x).begin(), (x).end()
#define SZ(x) static_cast<int>((x).size())
typedef long long ll;

const int MAXN = 30 + 5;
const int INF = 1e9 + 7;

namespace mcf {
const int MAXN = ::MAXN * ::MAXN * 4;
const int MAXM = MAXN;
struct Edge {
    int v, c, f, nxt;
}E[MAXM << 1];
int S, T;
ll C, F, Dis[MAXN];
int H[MAXN], cntE;
int Lp[MAXN], Le[MAXN];
void addEdge(int u, int v, int f, int c) {
    E[++cntE] = (Edge) {v, c, f, H[u]};
    H[u] = cntE;
    E[++cntE] = (Edge) {u, -c, 0, H[v]};
    H[v] = cntE;    
}
bool spfa() {
    static std::bitset<MAXN> Inq;
    static std::queue<int> Que;
    Inq = 0;
    memset(Dis, 0x3f, sizeof Dis);
    Dis[S] = 0;
    Que.push(S);
    while(!Que.empty()) {
        int x = Que.front(); Que.pop();
        Inq[x] = false;
        for(int i = H[x]; ~i; i = E[i].nxt) {
            int &v = E[i].v;
            if(E[i].f && Dis[v] > Dis[x] + E[i].c) {
                Dis[v] = Dis[x] + E[i].c;
                Lp[v] = x, Le[v] = i;
                if(!Inq[v]) {
                    Inq[v] = true;
                    Que.push(v);
                }
            }
        }
    }
    return Dis[T] < 0;
}
void mcf() {
    while(spfa()) {
        int f = INF;
        for(int i = T; i != S; i = Lp[i]) {
            f = std::min(f, E[Le[i]].f);
        }
        C += f * Dis[T];
        F += f;
        for(int i = T; i != S; i = Lp[i]) {
            E[Le[i]].f -= f;
            E[Le[i] ^ 1].f += f;
        }
    }
}
void init() {
    memset(H, -1, sizeof H);
    cntE = -1;
    C = F = 0;
}
bool check() {
    for(int i = 0; i <= cntE; i += 2) {
        if(E[i].c == INF && E[i ^ 1].f > 0) {
            return false;
        }
        if(E[i].c == -INF && E[i].f > 0) {
            return false;
        }
    }
    return true;
}
}

int N, M;
int Type[MAXN][MAXN];
int Column[MAXN][MAXN], Line[MAXN][MAXN], Ori[MAXN][MAXN];
int ChangeC[MAXN][MAXN], ChangeL[MAXN][MAXN], ChangeO[MAXN][MAXN];
int IdC[MAXN][MAXN], IdL[MAXN][MAXN];
int Left[MAXN][MAXN], Up[MAXN][MAXN];
int AfterC[MAXN][MAXN], AfterL[MAXN][MAXN], AfterO[MAXN][MAXN];

int main() {
    mcf::init();
    int cnt = 0;
    scanf("%d%d", &N, &M);
    rep(i, 1, N + 1) {
        rep(j, 1, M + 1) {
            scanf("%d", &Type[i][j]);
        }
    }
    rep(i, 1, N + 1) {
        rep(j, 1, M + 1) {
            if(Type[i][j] == 1 || Type[i][j] == 3) {
                scanf("%d", &Column[i][j]);
                IdC[i][j] = ++cnt;
            }
            if(Type[i][j] == 2 || Type[i][j] == 3) {
                scanf("%d", &Line[i][j]);
                IdL[i][j] = ++cnt;
            }
            if(Type[i][j] == 4) {
                scanf("%d", &Ori[i][j]);
            }
        }
    }
    mcf::S = 0, mcf::T = cnt + 1;
    rep(i, 1, N + 1) {
        rep(j, 1, M + 1) {
            if(Type[i][j] == 1 || Type[i][j] == 3) {
                scanf("%d", &ChangeC[i][j]);
                if(ChangeC[i][j] == -1) {
                    ChangeC[i][j] = INF;
                }
            }
            if(Type[i][j] == 2 || Type[i][j] == 3) {
                scanf("%d", &ChangeL[i][j]);
                if(ChangeL[i][j] == -1) {
                    ChangeL[i][j] = INF;
                }
            }
            if(Type[i][j] == 4) {
                scanf("%d", &ChangeO[i][j]);
                if(ChangeO[i][j] == -1) {
                    ChangeO[i][j] = INF;
                }
            }
        }
    }
    rep(i, 1, N + 1) {
        rep(j, 1, M + 1) {
            if(Type[i][j] == 1 || Type[i][j] == 3) {
                int k = i + 1;
                while(k <= N && Type[k][j] == 4) {
                    Up[k++][j] = IdC[i][j];
                }
                AfterC[i][j] = k - i - 1;
                mcf::C += 1ll * ChangeC[i][j] * std::abs(AfterC[i][j] - Column[i][j]);
            }
            if(Type[i][j] == 2 || Type[i][j] == 3) {
                int k = j + 1;
                while(k <= M && Type[i][k] == 4) {
                    Left[i][k++] = IdL[i][j];
                }
                AfterL[i][j] = k - j - 1;
                mcf::C += 1ll * ChangeL[i][j] * std::abs(AfterL[i][j] - Line[i][j]);
            }
            if(Type[i][j] == 4) {
                AfterO[i][j] = 1;
                mcf::C += 1ll * ChangeO[i][j] * std::abs(AfterO[i][j] - Ori[i][j]);
            }
        }
    }
    rep(i, 1, N + 1) {
        rep(j, 1, M + 1) {
            if(Type[i][j] == 1 || Type[i][j] == 3) {
                if(AfterC[i][j] < Column[i][j]) {
                    mcf::addEdge(mcf::S, IdC[i][j], Column[i][j] - AfterC[i][j], -ChangeC[i][j]);
                }
                mcf::addEdge(mcf::S, IdC[i][j], INF, ChangeC[i][j]);
            }
            if(Type[i][j] == 2 || Type[i][j] == 3) {
                if(AfterL[i][j] < Line[i][j]) {
                    mcf::addEdge(IdL[i][j], mcf::T, Line[i][j] - AfterL[i][j], -ChangeL[i][j]);
                }
                mcf::addEdge(IdL[i][j], mcf::T, INF, ChangeL[i][j]);
            }
            if(Type[i][j] == 4) {
                if(AfterO[i][j] < Ori[i][j]) {
                    mcf::addEdge(Up[i][j], Left[i][j], Ori[i][j] - AfterO[i][j], -ChangeO[i][j]);
                }
                mcf::addEdge(Up[i][j], Left[i][j], INF, ChangeO[i][j]);
            }
        }
    }
    mcf::mcf();
    if(!mcf::check()) {
        printf("-1\n");
    } else {
        printf("%lld\n", mcf::C);
    }
    return 0;
}