自动搬运

查看原文

来自洛谷，原作者为

	Acestar Seadlev

搬运于2025-08-24 22:00:36，当前版本为作者最后更新于2020-02-26 17:41:36，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

upd: 修改了部分解释不清楚的地方以及 $Latex$

---

博客食用效果更佳 qaq

先来看看数据范围，就发现可以骗到分。

$\bold{40pts:}$

测试点1、2：$n,m≤1000$，直接 $O(nm)DP$。

测试点3、4：没有施工路口，直接 $C_{n+m}^n$ 求总方案数，然后因为 $P$ 是质数，所以用逆元取模即可。

$\bold{60pts:}$

测试点5、6：因为 $P$ 不是质数，所以把 $P$ 分解成几个质数的乘积，分别算出 $C_{n+m}^n$ 对每个质数取模的结果，然后用 中国剩余定理$(CRT)$ 合并求解（中国剩余定理下面会讲）。

以上就是考场上的骗分思路。

---

$\bold{100pts:}$

把每个施工路口的坐标存进 $pos$ 结构体数组，再把 $(n,m)$ 存进 $pos_{t+1}$，然后将 $pos$ 按 $x$ 从小到大排序，如果 $x$ 相等，就按 $y$ 从小到大排序。

用 $f_i$ 表示从 $(0,0)$ 到 $(pos_i.x,pos_i.y)$ 并且不经过其他施工路口的方案数，然后大力推式子：

这里为了方便表示，将 $(pos_i.x,pos_i.y)$ 改为 $(x_i,y_i)$

$$f_i=C_{x_i+y_i}^{x_i}-\sum_{j=1}^{t}f_jC_{x_i-x_j+y_i-y_j}^{x_i-x_j}\ \ \text{(符合条件的j)} $$

其中，

第一项表示从 $(0,0)$ 到 $(x_i,y_i)$ 的总方案数。

第二项表示所有所有符合要求的 $j$ 从 $(0,0)$ 到 $(x_i,y_i)$ 且不经过其他施工路口的方案数 × 从$(x_j,y_j)$ 到 $(x_i,y_i)$ 的方案数的和。

显然，$j$ 的条件是 $x_j\le x_i,y_j\le y_i$。

由于已经将 $pos$ 数组排了序，所以式子中 $j$ 的范围可以缩小到 $i-1$ ：

$$f_i=C_{x_i+y_i}^{x_i}-\sum_{j=1}^{i-1}f_jC_{x_i-x_j+y_i-y_j}^{x_i-x_j}\ \ (x_j\le x_i,y_j\le y_i) $$

举个例子（样例）：

已知 $f_1=2$ 求 $f_2:$

$f_2=C_4^2-f_1×C_2^1$

$\quad\ =6-2×2$

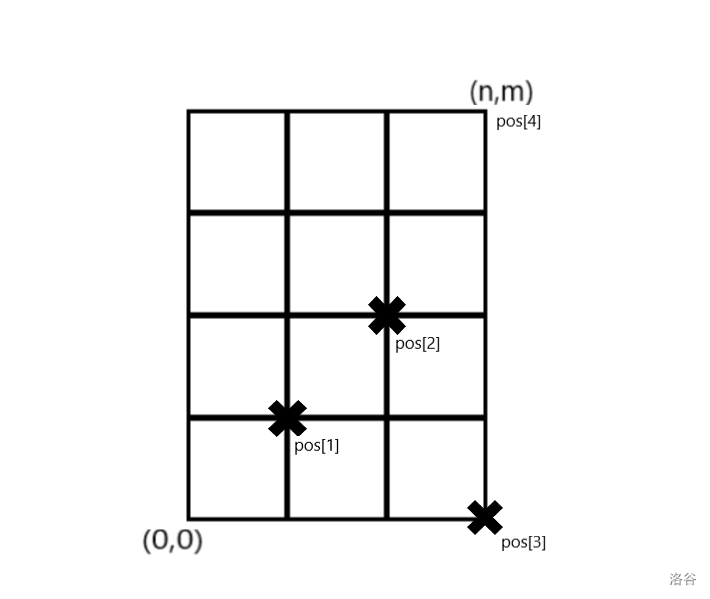
$\quad\ =2$

其余同理。

最后输出 $f_t$ 即可。

至此，本题的主体思路已经讲完了。

---

接下来考虑怎么计算 $C_n^m\bmod P$。

因为 $P$ 不一定是质数，所以不能直接用逆元取模。

当 $P$ 是质数的时：

直接用 $Lucas$ 即可。

$C_n^m=C_{n\bmod{p}}^{m\bmod{p}}×C_{n/p}^{m/p}\bmod{p}$

当 $P$ 不是质数时：

如何处理上面已经提到了，就是把 $P$ 分解成几个质数的积，存进 $p$ 数组，再用 $CRT$ 合并。

先介绍一下 $CRT:$

设 $m_1,m_2,...,m_n$ 是两两互质的整数，$m=∏_{i=1}^nm_i$，$M_i=\dfrac{m}{m_i}$，$t_i$是线性方程$M_it_i≡1(mod\ m_i)$ 的一个解（也就是逆元）。

对于任意的 $n$ 个整数 $a_1,a_2,...,a_n,$ 方程组

$\begin{cases} x≡a_1\ (\bmod{m_1})&\\ x≡a_2\ (\bmod{m_2})&\\ ...\ &\\ x≡a_n\ (\bmod{m_n}) \end{cases}$

有整数解，解为 $x=\sum_{i=1}^na_iM_it_i$。

证明请左转自行百度。

本题中 $P=1019663265=3×5×6793×10007$

令 $p_1=3,\ p_2=5,\ p_3=6793,\ p_4=10007$，显然它们两两互质，符合上述 $CRT$ 中的 $m$ 数组。

$a_i=C_n^m \bmod p_i$ 这里就可以逆元了

---

已经能求出 $C_n^m\bmod{P}$ 了。

然后再用 $DP$ 转移出最后的结果。

复杂度 $O(T^2\log n)$

上代码:

#include <bits/stdc++.h>
#define ll long long
#define db double
#define gc getchar
#define pc putchar

using namespace std;

namespace IO
{
    template <typename T>
    void read(T &x)
    {
        x = 0; bool f = 0; char c = gc();
        while(!isdigit(c)) f |= c == '-', c = gc();
        while(isdigit(c)) x = x * 10 + c - '0', c = gc();
        if(f) x = -x;
    }

    template <typename T>
    void write(T x)
    {
        if(x < 0) pc('-'), x = -x;
        if(x > 9) write(x / 10);
        pc('0' + x % 10);
    }
}
using namespace IO;

const int N = 1e6 + 5;

struct node
{
    int x, y;
}pos[210];
int n, m, t, P, tp;
int f[210], g[5], p[5], mul[5], fac[5][N], invm[5], inv[5][N];

inline bool cmp(node a, node b)
{
    return a.x == b.x ? a.y < b.y : a.x < b.x;
}

inline int power(int a, int b, int p)
{
    int ret = 1;
    a %= p;
    while(b)
    {
        if(b & 1) ret = 1ll * ret * a % p;
        a = 1ll * a * a % p, b >>= 1;
    }
    return ret;
}

inline int C(int a, int b, int i)       //C(a, b) % i
{
    if(a < b) return 0;
    if(!b || a == b) return 1;
    if(a < p[i] && b < p[i]) return 1ll * fac[i][a] * inv[i][b] % p[i] * inv[i][a - b] % p[i];
    return 1ll * C(a % p[i], b % p[i], i) * C(a / p[i], b / p[i], i) % p[i];
}

inline int CRT(int a, int b)        //中国剩余定理 
{
    if(!tp) return C(a, b, 0);      //P为质数时直接返回C(a,b)%p[0] 
    int ret = 0;
    for(int i = 1; i <= 4; i++) g[i] = C(a, b, i);    //g[i]=C(a,b)%p[i] 
    for(int i = 1; i <= 4; i++) ret = (ret + 1ll * g[i] * mul[i] % P * invm[i] % P) % P;
    return ret;
}

int main()
{
    read(n), read(m), read(t), read(P);
    for(int i = 1; i <= t; i++)
        read(pos[i].x), read(pos[i].y);
    pos[++t] = (node) {n, m};        //将(n,m)加到pos[t+1]
    sort(pos + 1, pos + 1 + t, cmp); //排序

    if(P == 1e6 + 3) p[0] = P;      //如果P是质数，存到p[0]
    else p[1] = 3, p[2] = 5, p[3] = 6793, p[4] = 10007, tp = 1; //否则，分解成4个质数，并且tp=1,表示P不是质数

    //预处理
    if(tp)  //如果P不是质数
    {
        for(int i = 1; i <= 4; i++)
        {
            mul[i] = P / p[i]; //CRT 中的 m 数组
            invm[i] = power(mul[i], p[i] - 2, p[i]); //mul[i] % p[i] 的逆元
            fac[i][0] = 1; //0! % p[i]

            for(int j = 1; j < p[i]; j++)
                fac[i][j] = 1ll * fac[i][j - 1] * j % p[i]; //j! % p[i]

            inv[i][p[i] - 1] = power(fac[i][p[i] - 1], p[i] - 2, p[i]); //(p[i]-1)! % p[i] 的逆元

            for(int j = p[i] - 1; j >= 1; j--)
                inv[i][j - 1] = 1ll * inv[i][j] * j % p[i]; //逆元的递推
        }
    }
    else
    {
        //同上，只是少一层循环，因为只有一个质数
        fac[0][0] = 1;
        for(int i = 1; i < P; i++)
            fac[0][i] = 1ll * fac[0][i - 1] * i % P;

        inv[0][P - 1] = power(fac[0][P - 1], P - 2, P);
        for(int i = P - 1; i >= 1; i--)
            inv[0][i - 1] = 1ll * inv[0][i] * i % P;
    }

    for(int i = 1; i <= t; i++) {
        f[i] = CRT(pos[i].x + pos[i].y, pos[i].x); //从(0,0)到(pos[i].x,pos[i].y)的总方案数

        //减去经过其他施工路口的方案数
        for(int j = 1; j < i; j++)
            if(pos[j].x <= pos[i].x && pos[j].y <= pos[i].y)
                f[i] = (f[i] - 1ll * f[j] * CRT(pos[i].x - pos[j].x + pos[i].y - pos[j].y, pos[i].x - pos[j].x) % P + P) % P;
    }

    write(f[t]), pc('\n');
    return 0;
}

题外话：

我在写这篇题解的时候，浏览器突然就未响应了，所以就重新写了一遍 qwq，建议大家如果没有 typora 或 vscode 等软件可以先在云剪贴板上写好了复制过来。