1 条题解
-
0
自动搬运
来自洛谷,原作者为

三点水一个各
卷不动了搬运于
2025-08-24 22:00:32,当前版本为作者最后更新于2020-10-29 11:27:47,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
本题出现公共后缀,考虑将所有单词放在一棵树里做。
什么是Trie
Trie 亦称字典树、前缀树,是一种以空间换时间的做法。
对于一个长度为 的字符串,插入和查询的复杂度均为 。
如图所示,将 放入 Trie。
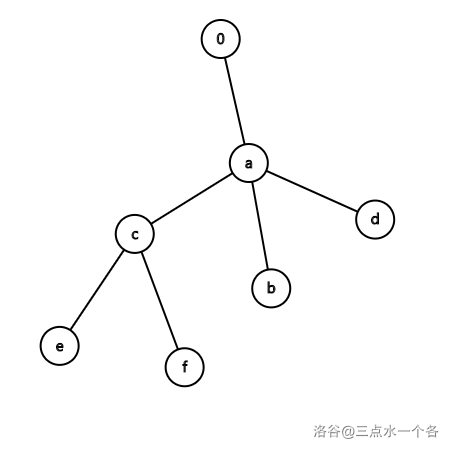
详细的 Trie 插入和查询操作请完成模板题P2580。
建树
观察本题,需要找到公共后缀,所以将单词反向存入 Trie,如图所示,将 放入 Trie。

题面写到,序列中相邻两个单词需满足 ,所以相邻两个单词要么是父子关系,要么是兄弟关系,如:
和 是父子关系(当然顺序可以调换, 和 也是合法的);
和 是兄弟关系(同理可以调换顺序, 和 也是合法的)。
所以,我们可以确定在图中的访问顺序是以下三种:访问父结点,访问子结点,访问同父的兄弟结点,如下图所示:
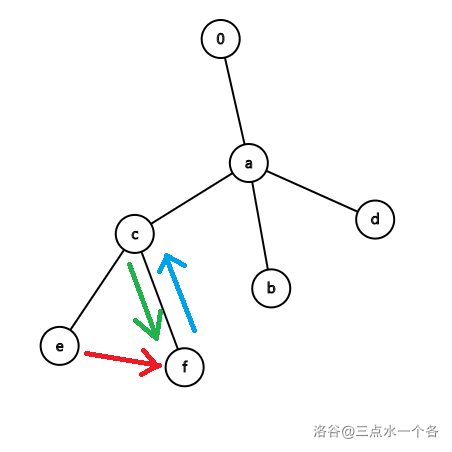
随后我们发现,在建树的过程中,不是所有结点都能按照如上三种顺序访问,如对 建树时,结点 不能到结点 ,因为并不存在 这个单词,如图所示:
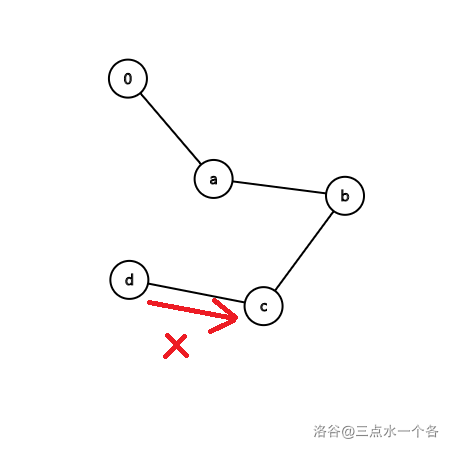
所以对于每个结点,我们用一个 数组来存储他们出现的次数,当然,由于
所有单词互不相同,这个数值只可能是 或 。对 建树时,如图所示:
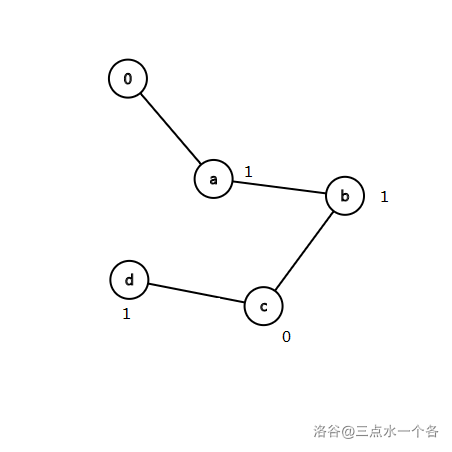
至此,建树完毕。
查找
我们知道,在查找过程中,因为出现次数为 的点不可以被经过,所以不会出现 脱 节 的现象。
并且由于
所有单词互不相同,所以不走回头路,即同一结点不经过 次。所以最后所有序列构成的图是一棵树而不是森林。
如图是对于 一种可能的情况:
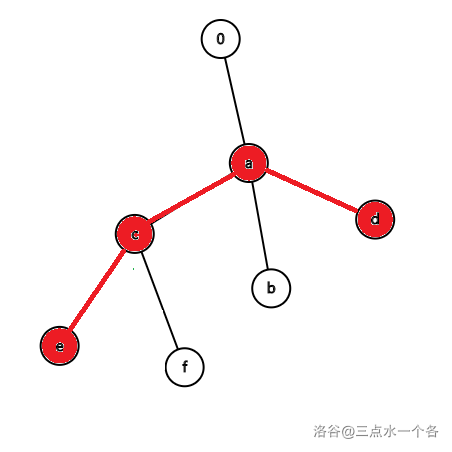
因此在一种可能的情况中,一个结点可能作为根结点,也可能是非根结点。
下面我先将情况理想化:
- 所有结点 所代表的单词次数均为 ,即 。
- 该结点是非根结点。
- 不考虑该结点以上的结点(包括其父结点)
开一个数组,记 结点作为非根结点时能取得最大单词数为 。
首先,因为兄弟结点互相之间可以连接,并且访问顺序可以随意,在这里将所有的子节点 都取来(取的是结点 本身,而不是 )。
然后,思考对于 的子结点 ,在访问到 之前,肯定是由 以下的结点过来的,也就是由 个结点过来的,要使 最大,就得找到最大的 。
(这里 的关系有点复杂,总之就是 是 的子结点, 是 作为非根结点时能取得最大单词数,请读者自行梳理)。
最后可以取到 结点本身,不要漏掉。
设 有 个子结点,那么
至于为什么是 而不是 ,是因为 在 和 中均出现一次。
举个例子:
对于单词 $\texttt{ba},\texttt{da},\texttt{eca},\texttt{fca},\texttt{ica},\texttt{heca},\texttt{geca},\texttt{jfca}$,以 为非根结点时,如图所示:
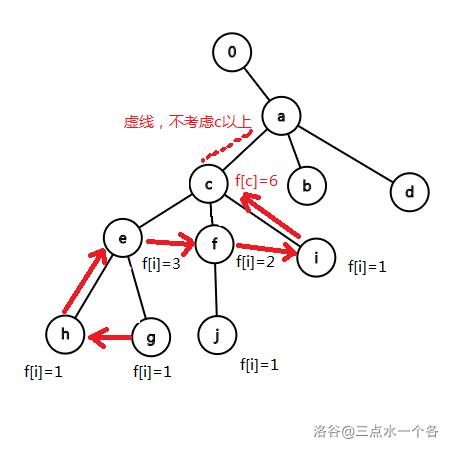
解释一下,此图中, 子节点个数 ,子节点(,,)中最大的 为 ,故 。
为什么 只能取子结点 中最大的一个 而不是取多个?
因为如果取第二个,意味着从一个叶子结点(如 , )经过 到另一个叶子结点(如),此时无法再从叶子结点往上,因为
所有单词互不相同,那么此时, 就成了根节点,与我的假设不符。如图所示: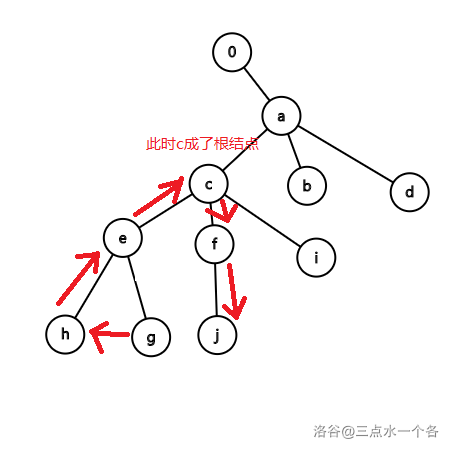
接下来考虑当该结点为根结点:
上面分析非根结点说过,如果取第二个,意味着该结点就是根结点。
所以以该点为根节点时,最大单词个数是在以该单词为非根结点的基础上,再加上第二大的 ,即:
接下来考虑该结点对应单词个数为 ,即 :
对于一个对应单词个数为 的结点,不能将它忽略。
因为如果他存在对应单词个数不为 的子结点,即 。
这些 的子结点之间扔可以相互访问,
这是只需要把公式中最后加上去的 删掉就可以了。
复杂度
设单词个数为 ,长度之和为 。
建树复杂度 。
查找复杂度 。
#include<bits/stdc++.h> using namespace std; int a[2000003][27],b[2000003],f[2000003];//3e6似乎要炸 int n,m,l1,l2,num=0,ans=0; string s; int main() { scanf("%d",&n); memset(a,0,sizeof(a)); for(int k=1;k<=n;++k) //Trie 建树 { int x=0; cin>>s; for(int i=s.length()-1;i>=0;--i) { if(!a[x][s[i]-'a']) a[x][s[i]-'a']=++num; x=a[x][s[i]-'a']; } b[x]++; //单词个数 } for(int i=num;i>=0;--i) { f[i]=b[i]; //该节点单词个数,是1或是0 l1=l2=0; //最大和次大 for(int j=0;j<=25;++j) if(b[a[i][j]]) //存在该子结点,若该结点对应单词数为0,没有意义。 { f[i]++; //选取子结点本身 if(f[a[i][j]]-1>l1) l2=l1,l1=f[a[i][j]]-1; //更新最长 else if(f[a[i][j]]-1>l2) l2=f[a[i][j]]-1;//更新次长 } f[i]+=l1; //非根结点最多单词 ans=max(ans,f[i]+l2); //根节点最多单词。 } printf("%d",ans); return 0; }
- 1
信息
- ID
- 3438
- 时间
- 1000ms
- 内存
- 250MiB
- 难度
- 5
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
