自动搬运

查看原文

来自洛谷，原作者为

	xcxcli AFOed.

搬运于2025-08-24 22:00:16，当前版本为作者最后更新于2019-10-09 15:23:34，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

真是一道毒瘤的好题！

step1 预处理

设有三个正整数 $x,y,z$，满足 $xy=p^2,xz=q^2$，那么 $yz=(\frac{pq}x)^2$，也是完全平方数。

所以我们得到，若 $i,j$ 和 $j,k$ 不能相邻，则 $i,k$ 也不能相邻。所有球之间的不能相邻的关系构成了多个完全图。我们可以利用并查集合并每个图上的球。

那么我们将题意转化为：

有 $m$ 种颜色的球，第 $i$ 种颜色的球有 $s_i$ 个，求同色不相邻的排列的数量。

最后将球按颜色排序，本题的预处理就完成了。

step2 DP

本题的毒瘤之处就在与状态和转移。

先看状态定义：

$f[i][j][k]$ 表示在前 $i$ 个球的排列中，满足颜色不等于第 $i$ 个球且同色相邻的有 $j$ 对，颜色等于第 $i$ 个球且相邻的有 $k$ 对时，排列的方案数。

看到这里晕头转向的同学，这里有图让你清醒：

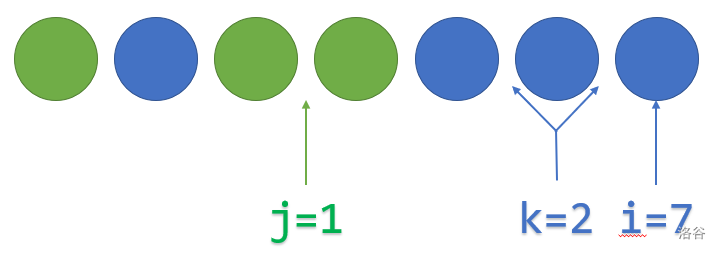
容易得到答案就是 $f[n][0][0]$。

下面为大家一条一条讲解状态转移方程。

转移1

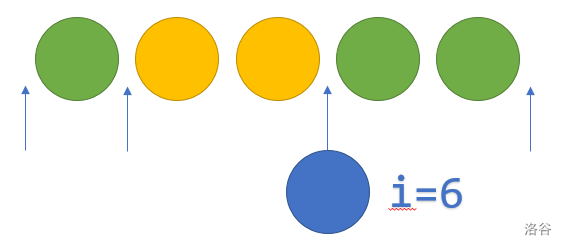
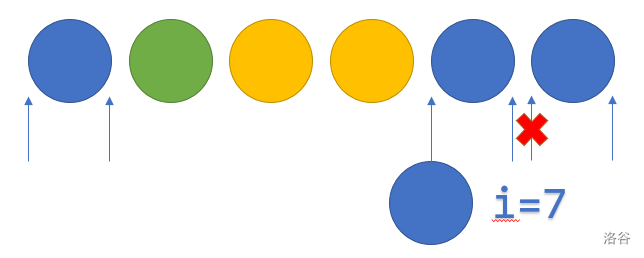
第 $i$ 个球与第 $i-1$ 个球颜色不同，将该球放于两个异色球之间（包括排列的开头和结尾）。

因为我们之前已经按颜色排序了，所以第 $i$ 个球的颜色还是第一次出现。如下图，$i=6,j=2,k=0$，此前的状态为 $i'=5=i-1,j'=1,k'=1=j-j'$（与 $i-1$ 不同色的连续块数 $=$ 现在的连续块数 $-$ 与 $i-1$ 同色的连续块数）。可以插入的位置数有$i-j=4$个。

所以 $f[i][j][0]+=f[i-1][j'][j-j']*(i-j)\quad j'\in[0,j]$

转移2

第 $i$ 个球与第 $i-1$ 个球颜色不同，将该球放于两个同色球之间。

如下图，$i=6,j=1,k=0$，此前的状态为 $i'=5=i-1,j'=1,k'=1=j-j'+1$，可以插入的位置有 $j+1=2$ 个。

所以 $f[i][j][0]+=f[i-1][j'][j-j'+1]*(j+1)\quad j'\in[0,j+1]$

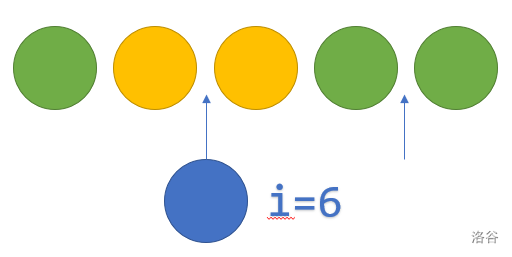
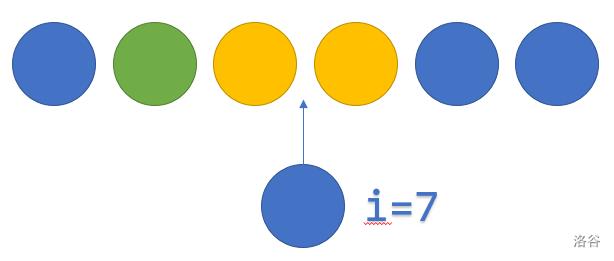
转移3

第 $i$ 个球与第 $i-1$ 个球颜色相同，将该球放于与该球颜色相同的球旁边。

为了方便，设到第 $i-1$ 个球有 $cnt$ 个与 $i$ 球颜色相同的球。如下图，$i=7,j=1,k=2,cnt=3$，此前的状态为 $i'=6=i-1,j'=1=j,k'=1=k-1$，符合条件的位置有 $cnt*2=6$ 个，但有 $k'=1$ 个位置重复了，所以可以插入的位置有 $cnt*2-k'=cnt*2-k+1=5$ 个。

所以 $f[i][j][k]+=f[i-1][j][k-1]*(cnt*2-k+1)\quad k\in[1,cnt]$

转移4

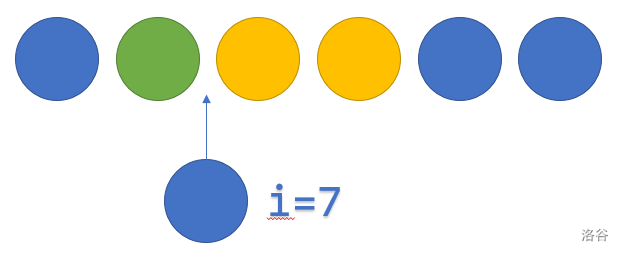
第 $i$ 个球与第 $i-1$ 个球颜色相同，将该球放于两个同色球之间。

如下图，$i=7,j=0,k=1,cnt=3$，此前的状态为 $i'=6=i-1,j'=1=j+1,k'=1=k$，可以插入的位置有 $j'=j+1=1$ 个。

所以 $f[i][j][k]+=f[i-1][j+1][k]*(j+1)\quad k\in[0,cnt]$

转移5

第 $i$ 个球与第 $i-1$ 个球颜色相同，将该球放于两个异色球之间。

如下图，$i=7,j=1,k=1,cnt=3$，此前的状态为 $i'=6=i-1,j'=1=j,k'=1=k$，可以插入的位置等于所有位置减去前面两种： $i-(cnt*2-k')-j'=i-cnt*2+k'-j'=i-cnt*2+k-j=1$。

所以 $f[i][j][k]+=f[i-1][j][k]*(i-cnt*2+k-j)\quad k\in[0,cnt]$

step3 复杂度、细节与代码

本题的时间复杂度为 $O(n^3)$，空间复杂度为 $O(n^3)$。下面的代码使用了滚动数组，将空间复杂度优化为 $O(n^2)$。

Code:

#include<stdio.h>
#include<math.h>
#include<string.h>
#include<algorithm>
#define ll long long
int rd(){
	int k=0;char c=getchar();
	while(c>'9'||c<'0')c=getchar();
	while(c>='0'&&c<='9')k=k*10+c-'0',c=getchar();
	return k;
}
const int N=301,M=1000000007;
int n,a[N],b[N],now=1,pre,cnt,f[2][N][N];//now,pre表示i和i-1的状态
bool sqr(ll x){ll S=sqrt(x);return S*S==x;}
int main(){
	freopen("data.in","r",stdin);
	freopen("data.out","w",stdout);
	n=rd();
	for(int i=1;i<=n;++i){
		a[i]=rd(),b[i]=i;
		for(int j=1;j<i;++j)if(sqr((ll)a[i]*a[j])){b[i]=j;break;}
	}//实际我们并不需要并查集，只用将父亲设为第一个匹配成完全平方数的数
	std::sort(b+1,b+n+1),f[0][0][0]=1;//初始化
	for(int i=1;i<=n;++i){
		memset(f[now],0,sizeof(f[now]));//滚动数组清空
		if(b[i]!=b[i-1]){
			cnt=0;//将与i相同的数的个数清空
			for(int j=0;j<i;++j)
				for(int k=0;k<=j+1;++k){//这里本来要枚举j'，为了方便写作k
					if(k<=j)f[now][j][0]=(f[now][j][0]+(ll)f[pre][k][j-k]*(i-j))%M;//注意边界
					f[now][j][0]=(f[now][j][0]+(ll)f[pre][k][j-k+1]*(j+1))%M;
				}
		}
		else{
			for(int j=0;j<i;++j)
				for(int k=0;k<=cnt;++k){
					if(k>0)f[now][j][k]=(f[now][j][k]+(ll)f[pre][j][k-1]*(cnt*2-k+1))%M;//注意边界
					f[now][j][k]=(f[now][j][k]+(ll)f[pre][j+1][k]*(j+1))%M;
					f[now][j][k]=(f[now][j][k]+(ll)f[pre][j][k]*(i-cnt*2+k-j))%M;
				}
		}
		now^=1,pre^=1,++cnt;//滚动
	}
	printf("%d\n",f[pre][0][0]);
	return 0;
}

step4 进阶算法

时隔一年重看这题，终于学会了容斥的 $O(n^2)$ 算法。

记颜色数为 $m$，第 $t$ 种颜色的球数量为 $s_t$。考虑所有合法与不合法情况，将相同颜色的球合并为一块，设合并后第 $t$ 种颜色的球块数为 $b_t$，记 $B=\sum\limits_{t=1}^mb_t$。

此时第 $t$ 种颜色的内部方案数为 $s_t!\binom{s_t-1}{b_t-1}$，即 $s_t$ 的任意排列乘上 $s_t$ 个球分为 $b_t$ 块的方案数。再考虑块之间的方案数量为 $\dfrac{B!}{\prod\limits_{t=1}^m(b_t!)}$，得到的结果为 $\dfrac{B!}{\prod\limits_{t=1}^m(b_t!)}\cdot\prod\limits_{t=1}^ms_t!\binom{s_t-1}{b_t-1}=(\prod\limits_{t=1}^m(s_t!))\cdot B!\prod\limits_{t=1}^m\binom{s_t-1}{b_t-1}\dfrac{1}{b_t!}$。

在计算时需要枚举所有的满足 $B=\sum\limits_{t=1}^mb_t$ 的 $b_t$，我们不妨设 $f(i,j)=\sum\limits_{b_i}\left([\sum\limits_{t=1}^ib_t=j]\prod\limits_{t=1}^i\binom{s_t-1}{b_t-1}\dfrac{1}{b_t!}\right)$，则结果为 $(\prod\limits_{t=1}^m(s_t!))\cdot B!f(m,B)$。

我们可以发现，有许多方案被错误计算了，如 1 1 2 这种方案会被 $f(2,3)$ 计算到，但这其实只分成了两块。于是我们可以容斥，最终答案 $ans=(\prod\limits_{t=1}^m(s_t!))\sum\limits_{B=m}^nB!f(m,B)(-1)^{n-B}$。

接下来只用考虑如何计算 $f(i,j)$，我们可以枚举 $b_i$，则 $f(i,j)=\sum\limits_{k=1}^{\min(s_i,j)}f(i-1,j-k)*\binom{s_t-1}{k-1}\frac1{k!}$。

考虑时间复杂度，虽然有三重循环，但循环次数为 $\sum\limits_{i=1}^ms_i(\sum\limits_{j=1}^is_j)$，实际上是 $O(n^2)$。

Code:

#include<stdio.h>
#include<math.h>
typedef long long ll;
int rd(){
	int k=0;char c=getchar();
	while(c>'9'||c<'0')c=getchar();
	while(c>='0'&&c<='9')k=k*10+c-'0',c=getchar();
	return k;
}
const int N=301,M=1000000007;
bool sqr(ll x){ll s=sqrt(x);return s*s==x;}
int Pow(int x,int a){
	int s=1;
	while(a){
		if(a&1)s=(ll)s*x%M;
		x=(ll)x*x%M,a>>=1;
	}
	return s;
}
int n,m,ans,a[N],s[N],fac[N],inv[N],f[N][N];
int C(int n,int m){return(ll)fac[n]*inv[m]%M*inv[n-m]%M;}
int main(){
	n=rd(),fac[0]=inv[0]=f[0][0]=1;
	for(int i=1;i<=n;++i){
		int _=rd();fac[i]=(ll)fac[i-1]*i%M;
		for(int j=1;j<=m;++j)if(sqr((ll)_*a[j])){++s[j];goto End;}
		a[++m]=_,++s[m];End:;
	}
	inv[n]=Pow(fac[n],M-2);
	for(int i=n-1;i;--i)inv[i]=(ll)inv[i+1]*(i+1)%M;
	for(int i=1,_=0;i<=m;++i){
		_+=s[i];
		for(int j=1;j<=_;++j)for(int k=1;k<=s[i]&&k<=j;++k)
			f[i][j]=(f[i][j]+(ll)f[i-1][j-k]*C(s[i]-1,k-1)%M*inv[k])%M;
	}
	for(int i=m;i<=n;++i){
		int t=(ll)f[m][i]*fac[i]%M;
		if((n-i)&1)ans=(ans+M-t)%M;
		else ans=(ans+t)%M;
	}
	for(int i=1;i<=m;++i)ans=(ll)ans*fac[s[i]]%M;
	printf("%d\n",ans);
	return 0;
}