自动搬运

查看原文

来自洛谷，原作者为

	蒟蒻初音ミク 初音仍在，只是葱人已逝

搬运于2025-08-24 21:59:52，当前版本为作者最后更新于2019-08-24 16:28:30，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

广告

蒟蒻的blog

正文

题意：给定$n$个集合的大小，问在相邻集合没有交集的情况下，并集的最小大小

题解：集合思想（外带图形解释，生动而形象）

如果是一条链，那么直接贪心，找出最大的相邻数的和就是答案。但是这个是一个环，即要避免与1集合的冲突。那么考虑二分+$dp$

设二分出来的并集大小为$x$。

维护一个$minn[i]$：表示在不与集合i-1冲突的情况下，集合i与集合1的最小冲突数量。

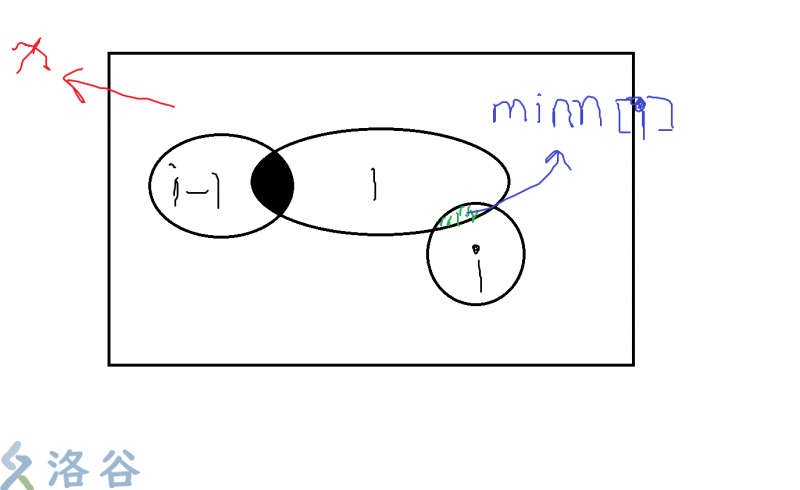
大概就是这个样子。。。

首先可以发现，不属于$i-1$集合也不属于$1$集合的元素是能选多少选多少的。由于求的是$minn[i]$，所以我们要使得$\{ i-1 \}∪ \{ 1 \}$的元素个数最小（因为这样的话能够不冲突的元素最多）而根据容斥原理（？？？），$\{ i-1 \}∪ \{ 1 \} = \{i-1 \}+ \{ 1 \}- \{ i-1 \}∩ \{1 \}$，即需要$\{ i-1 \}$与$\{ 1 \}$冲突数量最大

所以还需要一个$maxx[i]$：表示在不与集合$i-1$冲突的情况下，集合$i$与集合$1$的最大冲突数量

然后状态转移方程就特别好写了：

        maxx[i]=min(a[i],a[1]-minn[i-1]);
        minn[i]=max(0,a[i]-(x-(a[i-1]+a[1]-maxx[i-1])));

这里解释一下：

对于$minn[i]$，我们已经解释过了，但是对于$maxx[i]$，我们来看一下图：

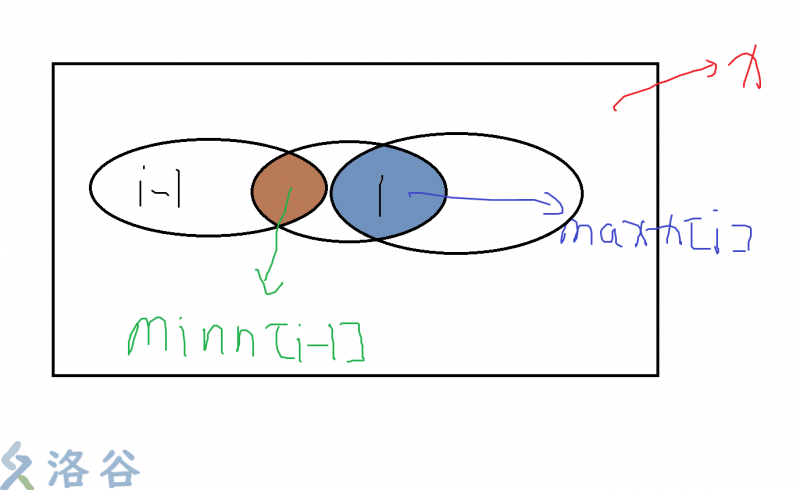
那么可以发现，$maxx[i]$其实就是把集合1剩下的部分全部占完（当然，可能占不完，因为最多占$a[i]$个），所以状态转移方程就是上面那个了。

最后贴一下代码，如果还有不懂的地方可以私信我哦~~~：

code:

#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
int n,a[100005],l,r,maxx[100005],minn[100005];
bool check(int x)
{
    for(int i=2;i<=n;i++)
    {
        maxx[i]=min(a[i],a[1]-minn[i-1]);
        minn[i]=max(0,a[1]+a[i-1]-maxx[i-1]+a[i]-x);
    }
    if(!minn[n]) return true;
    else return false;
}
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&a[i]);
        l=max(l,a[i]+a[i-1]);
    }
    maxx[1]=minn[1]=a[1];
    r=300000;
    while(l<=r)
    {
        int mid=(l+r)>>1;
        if(check(mid)) r=mid-1;
        else l=mid+1;
    }
    printf("%d",l);
    return 0;
}