自动搬运

查看原文

来自洛谷，原作者为

	C3H5ClO 金发吸血鬼赛高！

搬运于2025-08-24 21:59:52，当前版本为作者最后更新于2019-05-14 08:22:35，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

自己为贪心的合理性纠结了好久，题解里也没有严谨证明，我来写一下吧。

贪心的思路：找直径，直径端点为A,B,枚举C点则答案为$max(min(dis[A][k],dis[B][k])+dis[A][B])$

用反证法证明。

假设有一种情况，存在一条非直径路径DE，C先去D、E中距离较小点，再走过D、E间路径，所得的答案最大。

分两种情况讨论。

第一种情况，AB与DE有交点。

C与AB直接相连的情况如下图：

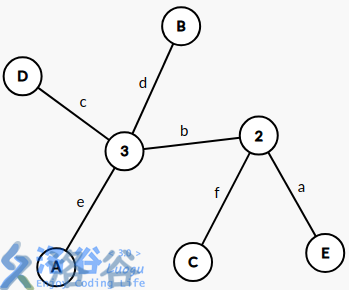
根据直径定义可知　$d+e>a+b+c,d+e\ge d+c,d+e\ge e+a+b$

整理可得

$d+e>a+b+c$------[1]

$e\ge c$------[2],

$d\ge a+b$------[3]

此时C点到A、B点的答案$S1=d+e+min(e+b+f,d+b+f)=d+e+b+f+min(e,d)$

C点到D、E点的答案$S2=a+b+c+min(f+a,f+b+c)=a+b+c+f+min(a,b+c)$

$S1-S2=d+e-a-b-c+b+min(e,d)-min(a,b+c)=(d+e-a-b-c)+min(d,e)-min(a-b,c)$

由[1]得$d+e-a-b-c>0$

当$a-b\le c$时,$S1-S2=(d+e-a-b-c)+min(d,e)-(a-b)$

由[2]得$e>c\ge a-b$,由[3]得$d\ge a+b\ge a-b$，因此此时$S1-S2>0$

当$a-b>c$时，$S1-S2=(d+e-a-b-c)+min(d,e)-c$

由[2]得$e\ge c$,由[3]得$d\ge a+b\ge a-b>c$，因此此时$S1-S2>0$

C与AB直接相连的情况同样类似。

第二种情况，AB与DE无交点。

由树的联通无环性可知AB与DE有且仅有一条路径相连，C与DE直接相连的情况如下图：

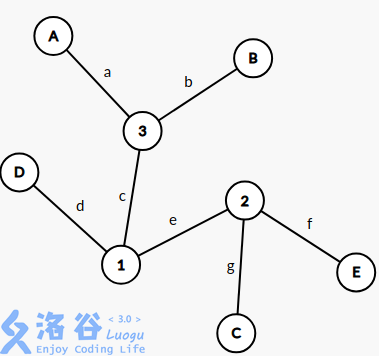
由直径的定义可知$a+b>d+e+f,a+b\ge c+d+b,a+b\ge a+c+e+f$

整理可得

$a+b>d+e+f$------[1]

$a\ge c+d$------[2]

$b\ge c+e+f$------[3]

此时C到A、B的答案$S1=a+b+min(a+c+e+g,b+c+e+g)=a+b+c+e+g+min(a,b)$

C到D、E的答案$S2=d+e+f+min(d+e+g,f+g)=d+e+f+g+min(d+e,f)$

$S1-S2=a+b-d-e-f+c+e+min(a,b)-min(d+e,f)=(a+b-d-e-f)+min(a,b)-min(d-c,f-e-c)$

由[1]得$a+b-d-e-f>0$

当$d-c\le f-e-c$时,$S1-S2=(a+b-d-e-f)+min(a,b)-(d-c)$

由[2]得$a\ge c+d>d-c$,由[3]得$b\ge c+e+f>f-e-c\ge d-c$,因此此时$S1-S2>0$

当$d-c>f-e-c$时,$S1-S2=(a+b-d-e-f)+min(a,b)-(f-e-c)$

由[2]得$a\ge c+d>d-c>f-e-c$,由[3]得$b\ge c+e+f>f-e-c$,因此此时$S1-S2>0$

C与$c$直接相连或与AB直接相连的情况类似。

综上，当DE不是直径时，总有一条C到直径AB的方案使答案更大，与假设C到DE的方案最大矛盾，因此假设不成立，原命题得证。

---

update:使用了LaTeX格式，对部分式子做了小改动，希望管理员给过