自动搬运

查看原文

来自洛谷，原作者为

	a2956331800 **

搬运于2025-08-24 21:59:50，当前版本为作者最后更新于2018-08-16 22:39:47，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

这个题很显然的扫描线

先枚举每条边把每个交点求出来，然后按交点的x坐标当扫描线，排序，答案即为相邻两条扫描线各种与三角形相交长度和*扫描线之间的距离/2（扫描线之间的三角形部分都是梯形）

每条扫描线求出它经过了多少面积，求的时候依次枚举每个三角形，求和三边是否有交，如果交点超过一个（可以不判是不是同一个点，因为如果是扫描线和三角形的一个点相交，计入答案的长度是0），就把两个交点之间的线段存成pair（y小的当first），然后把所有的相交线段排序，扫描总面积

扫描的时候记录一个当前区间，初始化为[-inf,-inf]，每次加入一个新线段时，如果新线段和当前区间无交，就把当前区间计入答案（由于按起点从小到大排序，之后不会再有区间和当前区间有交了），然后把记录的区间更新为新的区间，否则更新右端点（取max）

统计答案的核心代码：

double l=seg[1].x,r=seg[1].y,sum=0.0;
    for (int i=2;i<=cnt;++i)
    {
        if (seg[i].x-r>eps) sum+=r-l,l=seg[i].x,r=seg[i].y;
        else r=max(r,seg[i].y);
    }
    sum+=r-l;
    return sum;

然后如果按上面的思路做会WA第二个点以及第九个点可能出现各种错误 问题在于有一条边和y轴平行的边 比如这样的：

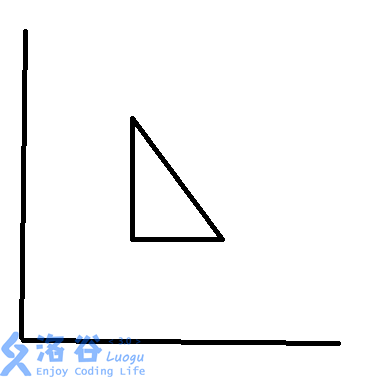
在扫描到它左边的时候会记录左边那个边的距离，但这条扫描线和前一条扫描线统计答案时这个边并不产生贡献，所以要特判这个，就是每条扫描线作为左边和右边的那条扫描线统计答案时要分别计算相交面积，如果发现这种三角形就特判一下是不是在当前统计答案的区域以外。

下面的代码里Minus是当左边的扫描线时统计答案的函数，Plus是当右边的扫描线时统计答案的函数，两个函数的差别在第四行的判断条件（输入时把三角形的三个点按x从小到大排序了），自己想象一下就知道差别在哪了

（我自己的代码有精度问题（应该是没有判eps的原因），开long double又会T一个，O2都救不了，就先放一个指导我写出代码的代码）

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
using namespace std;
#define N 105

const double eps=1e-12;
const double inf=1e9;
int dcmp(double x)
{
    if (x<=eps&&x>=-eps) return 0;
    return (x>0)?1:-1;
}
struct Vector
{
    double x,y;
    Vector(double X=0,double Y=0)
    {
        x=X,y=Y;
    }
    bool operator < (const Vector &a) const
    {
        return x<a.x||(x==a.x&&y<a.y);
    }
    void read(){scanf("%lf%lf",&x,&y);}
};
typedef Vector Point;
struct Line
{
    Point p,q;
    Line(Point P=Point(0,0),Point Q=Point(0,0))
    {
        p=P,q=Q;
    }
};
Vector operator + (Vector a,Vector b) {return Vector(a.x+b.x,a.y+b.y);}
Vector operator - (Vector a,Vector b) {return Vector(a.x-b.x,a.y-b.y);}
Vector operator * (Vector a,double b) {return Vector(a.x*b,a.y*b);}

int n,LSH;
double ans;
double lsh[N*N*10];
Point seg[N];
Line line[N][3];

double Cross(Vector a,Vector b)
{
    return a.x*b.y-a.y*b.x;
}
bool ins(Point A,Point B,Point C,Point D)
{
    Vector v,w,u;
    v=A-C,w=C-D,u=B-D;
    if (dcmp(Cross(v,w))==dcmp(Cross(u,w))) return 0;
    v=C-A,w=B-A,u=D-A;
    if (dcmp(Cross(v,w))==dcmp(Cross(u,w))) return 0;
    return 1;
}
Point GLI(Point P,Vector v,Point Q,Vector w)
{
    Vector u=P-Q;
    double t=Cross(w,u)/Cross(v,w);
    return P+v*t;
}
double Plus(double x)
{
    int cnt=0;
    for (int i=1;i<=n;++i)
    {
        if (dcmp(line[i][1].p.x-line[i][1].q.x)==0&&dcmp(x==line[i][1].p.x))
            continue;
        double Min=inf,Max=-inf;
        for (int j=1;j<=3;++j)
        {
            if (x<line[i][j].p.x||x>line[i][j].q.x) continue;
            if (dcmp(line[i][j].p.x-line[i][j].q.x)==0) continue;
            Point P=GLI(line[i][j].p,line[i][j].q-line[i][j].p,Point(x,-inf),Vector(0,inf));
            Min=min(Min,P.y),Max=max(Max,P.y);
        }
        if (Max-Min>eps) seg[++cnt]=Point(Min,Max);
    }
    sort(seg+1,seg+cnt+1);
    if (!cnt) return 0.0;
    double l=seg[1].x,r=seg[1].y,sum=0.0;
    for (int i=2;i<=cnt;++i)
    {
        if (seg[i].x-r>eps) sum+=r-l,l=seg[i].x,r=seg[i].y;
        else r=max(r,seg[i].y);
    }
    sum+=r-l;
    return sum;
}
double Minus(double x)
{
    int cnt=0;
    for (int i=1;i<=n;++i)
    {
        if (dcmp(line[i][2].p.x-line[i][2].q.x)==0&&dcmp(x==line[i][2].p.x))
            continue;
        double Min=inf,Max=-inf;
        for (int j=1;j<=3;++j)
        {
            if (x<line[i][j].p.x||x>line[i][j].q.x) continue;
            if (dcmp(line[i][j].p.x-line[i][j].q.x)==0) continue;
            Point P=GLI(line[i][j].p,line[i][j].q-line[i][j].p,Point(x,-inf),Vector(0,inf));
            Min=min(Min,P.y),Max=max(Max,P.y);
        }
        if (Max-Min>eps) seg[++cnt]=Point(Min,Max);
    }
    sort(seg+1,seg+cnt+1);
    if (!cnt) return 0.0;
    double l=seg[1].x,r=seg[1].y,sum=0.0;
    for (int i=2;i<=cnt;++i)
    {
        if (seg[i].x-r>eps) sum+=r-l,l=seg[i].x,r=seg[i].y;
        else r=max(r,seg[i].y);
    }
    sum+=r-l;
    return sum;
}
int main()
{
    scanf("%d",&n);
    for (int i=1;i<=n;++i)
    {
        Point A,B,C;A.read(),B.read(),C.read();
        if (A.x>B.x) swap(A.x,B.x),swap(A.y,B.y);
        if (B.x>C.x) swap(B.x,C.x),swap(B.y,C.y);
        if (A.x>B.x) swap(A.x,B.x),swap(A.y,B.y);
        lsh[++LSH]=A.x,lsh[++LSH]=B.x,lsh[++LSH]=C.x;
        line[i][1]=Line(A,B),line[i][2]=Line(B,C);line[i][3]=Line(A,C);
    }
    for (int i=1;i<=n;++i)
        for (int j=1;j<=3;++j)
            for (int k=i+1;k<=n;++k)
                for (int l=1;l<=3;++l)
                {
                    Point A=line[i][j].p,B=line[i][j].q,C=line[k][l].p,D=line[k][l].q;
                    if (ins(A,B,C,D))
                    {
                        Point q=GLI(A,B-A,C,D-C);
                        lsh[++LSH]=q.x;
                    }
                }
    sort(lsh+1,lsh+LSH+1);LSH=unique(lsh+1,lsh+LSH+1)-lsh-1;
    double last=0.0,now;
    for (int i=1;i<=LSH;++i)
    {
        now=Plus(lsh[i]);
        if (i>1) ans+=(now+last)*(lsh[i]-lsh[i-1])/2.0;
        last=Minus(lsh[i]);
    }
    printf("%.2lf\n",ans-eps);
}

代码来源传送门