自动搬运

查看原文

来自洛谷，原作者为

	chihik An Ac a day, keeps the doctor away!

搬运于2025-08-24 21:59:46，当前版本为作者最后更新于2019-10-22 20:53:11，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

这道题貌似很多人用的是网络流+分层图。这里介绍一种费用流解法。

可以证明，最后一个人到达的时间是小于第100天的。

那么对于每一趟航班，如果他的起点是$u$，终点为$v$，可搭乘的人的数量为$w$。那我们就对$(u,v)$连100条流量为$w$,费用为$i$的边（$i$表示第几天），分别表示第$i$天的航班。

我们跑费用流时，也不是计算最短距离，而是找到起点到终点的一条路径上的一条费用最大的边的最小值。

比如

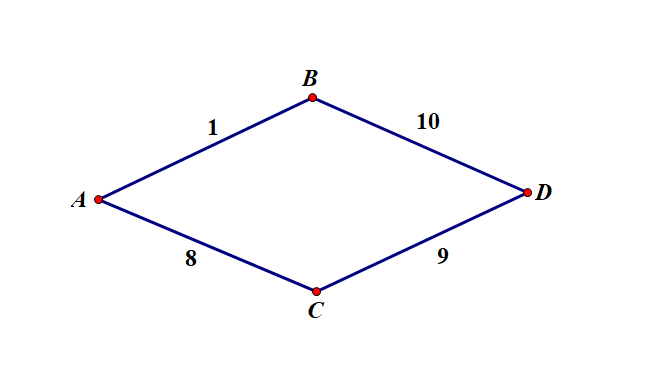
我们要的路径是$A \to C \to D$,因为$max(AC,CD)<max(AB,BD)$

跑一个流量为$t$的费用流即可。

#include <cstdio>
#include <queue>
#include <cstring>
using namespace std;
#define INF 0x3f3f3f3f

const int MAXN = 5005;
int flow , cost;
int n , m , u , v , w , f;
struct node{
	int v , w , f , rev;
};
vector< node > Graph[ MAXN + 5 ];

int dis[ MAXN + 5 ] , vis[ MAXN + 5 ];
int prevv[ MAXN + 5 ] , preve[ MAXN + 5 ];
void spfa( int s , int t ) {
	queue< int > Que;
	memset( dis , 0x3f , sizeof( dis ) );
	memset( vis , 0 , sizeof( vis ) );

	dis[ s ] = 0 , vis[ s ] = 1 , Que.push( s );
	while( !Que.empty( ) ) {
		int u = Que.front( );
		Que.pop( ) , vis[ u ] = 0;

		for( int i = 0 ; i < Graph[ u ].size( ) ; i ++ ) {
			int v = Graph[ u ][ i ].v , w = Graph[ u ][ i ].w;
			if( w <= dis[ u ] ) continue;	//保证一天只坐一班飞机
			if( Graph[ u ][ i ].f && dis[ v ] > max( dis[ u ] , w ) ) {
				dis[ v ] = max( dis[ u ] , w );
				prevv[ v ] = u , preve[ v ] = i;
				if( !vis[ v ] )
					Que.push( v ) , vis[ v ] = 1;
			}
		}
	}
}
void Costflow( int S , int T ) {
	while( 1 ) {
		spfa( S , T );
		if( !flow || dis[ T ] == INF ) return;
		
		int d = INF;
		for( int v = T ; v != S ; v = prevv[ v ] )
			d = min( d , Graph[ prevv[ v ] ][ preve[ v ] ].f );
		flow -= d , cost = max( cost , dis[ T ] );
		for( int v = T ; v != S ; v = prevv[ v ] ) {
			Graph[ prevv[ v ] ][ preve[ v ] ].f -=d;
			Graph[ v ][ Graph[ prevv[ v ] ][ preve[ v ] ].rev ].f += d;
		}
	}
}

int main( ) {
	scanf("%d %d %d",&n,&m,&flow);
	for( int i = 1 ; i <= m ; i ++ ) {
		scanf("%d %d %d",&u,&v,&f);
		for( int j = 1 ; j <= 105 ; j ++ ) {
			w = j;
			Graph[ u ].push_back( { v , w , f , Graph[ v ].size( ) } );
			Graph[ v ].push_back( { u , -w , 0 , Graph[ u ].size( ) - 1 } );
		}
	}
	Costflow( 1 , n );
	printf("%d\n",cost);
	return 0;
}

Update: 2021.1.5

深深的体会到 1 年前的自己太菜了。

考虑这道题的加强版：BZOJ4669 抢夺

唯一不同的是，这道题的人数很大，所以不能建分层图。

有两个显然的结论：

• 每天可以新到达的人数一定不降

• 后面的人可以跟着前面的人走，时间相差 1 天

但是可能过程中存在一条新的最短路，让这些跟别人走的人，通过新的最短路到达终点，这样就不会有 1 天的时差了。

所以每次增广后通过时间差值判断通过人数，无增广路之后用最大流计算。

为了保证尽量少的时间通过的人数多，用费用流增广。

这样做就不需要二分了。

如果你没有发现它是多测，就会像我一样爆零。

#include <cmath>
#include <queue>
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
#define Inf 0x3f3f3f3f

const int MAXN = 1000 , MAXM = 5000;
int head[ MAXN + 5 ] , Enum = 1;
struct Edge {
	int v , nxt , flw , w;
	Edge(){}
	Edge( int V , int Nxt , int Flw , int W ) { v = V , nxt = Nxt , flw = Flw , w = W; }
} Graph[ 2 * MAXM + 5 ];
void Add_Edge( int u , int v , int flw , int c ) {
	Graph[ ++ Enum ] = Edge( v , head[ u ] , flw ,  c ); head[ u ] = Enum;
	Graph[ ++ Enum ] = Edge( u , head[ v ] , 0   , -c ); head[ v ] = Enum;
}

int dis[ MAXN + 5 ]; bool inq[ MAXN + 5 ];
int cur[ MAXN + 5 ]; bool vis[ MAXN + 5 ];
bool Spfa( int s , int t ) {
	queue< int > Que;
	memset( dis , 0x3f , sizeof( dis ) );
	memset( inq , 0 , sizeof( inq ) );
	memset( vis , 0 , sizeof( vis ) );
	memcpy( cur , head , sizeof( head ) );
	dis[ s ] = 0; Que.push( s ) , inq[ s ] = 1;
	while( !Que.empty() ) {
		int u = Que.front();  Que.pop() , inq[ u ] = 0;
		for( int i = head[ u ] ; i ; i = Graph[ i ].nxt ) {
			int v = Graph[ i ].v , flw = Graph[ i ].flw , w = Graph[ i ].w;
			if( flw && dis[ v ] > dis[ u ] + w ) {
				dis[ v ] = dis[ u ] + w;
				if( !inq[ v ] ) Que.push( v ) , inq[ v ] = 1;
			}
		}
	}
	return dis[ t ] != Inf;
}
int dfs( int u , int t , int f ) {
	if( u == t ) return f; vis[ u ] = 1;
	for( int &i = cur[ u ] ; i ; i = Graph[ i ].nxt ) {
		int v = Graph[ i ].v , flw = Graph[ i ].flw , w = Graph[ i ].w;
		if( flw && dis[ v ] == dis[ u ] + w && !vis[ v ] ) {
			int mf = dfs( v , t , min( f , flw ) );
			if( mf ) {
				Graph[ i ].flw -= mf , Graph[ i ^ 1 ].flw += mf;
				return mf;
			}
		}
	} dis[ u ] = Inf;
	return 0;
}

int n , m , k , s , t;
int main( ) {
    // freopen("snatch.in","r",stdin);
    // freopen("snatch.out","w",stdout);

    while( ~scanf("%d %d %d",&n,&m,&k) ) {
        memset( head , 0 , sizeof( head ) ); Enum = 1;

        s = 1 , t = n;
        for( int i = 1 , u , v , c ; i <= m ; i ++ ) {
            scanf("%d %d %d",&u,&v,&c);
            Add_Edge( u , v , c , 1 );
        }

        if( k == 0 ) { printf("0\n"); }
        else {
            int Maxf = 0 , last = 0;
            for( ; Spfa( s , t ) ; last = dis[ t ] ) {
                int nowf = 0; for( int fl = 0 ; ( fl = dfs( s , t , Inf ) ) != 0 ; nowf += fl );

                if( k <= ( dis[ t ] - last ) * Maxf ) { 
                    printf("%d\n", last - 1 + (int)ceil( k * 1.0 / Maxf ) ) & 0;
                    goto there;
                }

                k -= ( dis[ t ] - last ) * Maxf;
                Maxf += nowf;
            }
            if( last == 0 ) { puts( "No solution" ); goto there; }
            printf("%d\n", last - 1 + (int)ceil( k * 1.0 / Maxf ) ) & 0;
        }
        there:;
    }
    return 0;
}