自动搬运

查看原文

来自洛谷，原作者为

	juruo999 “如若此后千百年来,来人漫步于繁星身侧,人们便要赞颂她的名。”

搬运于2025-08-24 21:59:37，当前版本为作者最后更新于2021-12-04 11:38:51，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

P4385 Dvapravca 题解

我的Blog
样例演示1
样例演示2

给定 $n$ 个红色或蓝色的点，三点不共线，求中间没有蓝点的两条平行线间最多能有几个红点。

显然，两条平行线一定不会是两点间的连线，否则将平行线旋转足够小的角度 $\delta$ 后可以得到另一个更优的解。

假设两条平行线都垂直于直线 $l$，过每个点作 $l$ 的垂线，得到 $n$ 个点，那么问题就转化为求投影序列上的最长连续红色子段。样例演示1 可以很直观的解释这个思路。

考虑动态维护这个序列。找出这 $n$ 个点间的所有连线，当 $l$ 垂直于连线时，就交换连线两端的点对应的颜色。看下面这张图就可理解。

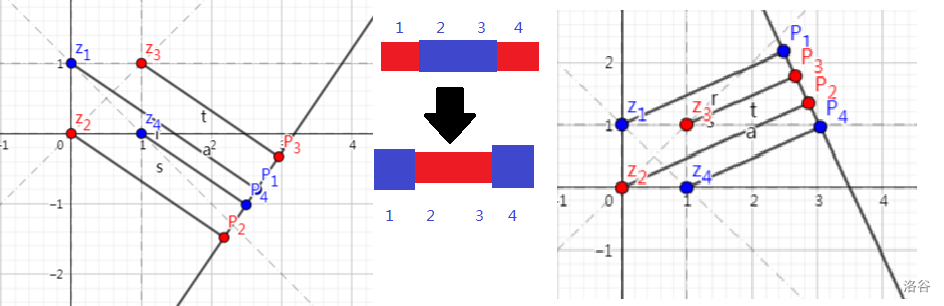
当你理解这一步时，你已经能做出这道题了。

用线段树维护最长连续零个数，时间复杂度 $O(n^2\log n)$。

P.S. 不用线段树，暴力维护连续零加上 O2 也能 AC……主要是我线段树写挂了！

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<vector>
#include<queue>

using namespace std;

#define il inline
typedef long long ll;

ll gcd(ll a,ll b){
	return b==0?a:gcd(b,a%b);
}

typedef double Grad;

int n;
struct Node{
	int x,y;
	int p;
	char c;
}a[1005];
bool cmp(Node a,Node b){
	return a.x!=b.x?a.x<b.x:a.y>b.y;
}

int s[1005];

struct Line{
	int i1,i2;	// id
	Grad G;
	Line(){} Line(int a_,int b_){i1=a_,i2=b_;G=1.0*(a[i2].y-a[i1].y)/(a[i2].x-a[i1].x);}
	bool operator<(Line b){
		return G<b.G;
	}
}ls[1000006];
int ms=0;

vector<pair<int,int> > sw[1000006];int st;

int did[1006],id[1006];

int main(){

	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		scanf("%d%d",&a[i].x,&a[i].y);
		a[i].c=getchar(); while(a[i].c!='R' && a[i].c!='B'){ a[i].c=getchar(); }
	}
	sort(a+1,a+n+1,cmp);
	
	for(int i=1;i<=n;i++){
		s[i]=((a[i].c=='R')?0:1);
	}

	for(int i=1;i<=n;i++){
		for(int j=i+1;j<=n;j++){
			ls[++ms]=Line(i,j);
		}
	}
	sort(ls+1,ls+ms+1);
	st=1;sw[1].push_back(make_pair(ls[1].i1,ls[1].i2));
	for(int i=2;i<=ms;i++){
		if(ls[i].G!=ls[i-1].G){
			st++;
		}
		sw[st].push_back(make_pair(ls[i].i1,ls[i].i2));
	}
   
	int ans=0;
	int l=1;		// 永远焕发光芒的暴力维护区间
	for(int j=1;j<=n;j++){
		if(s[j]==1){
			l=j+1;
		}
		if(s[l]==0 && s[j]==0){ans=max(ans,j-l+1);}
	}

	for(int i=1;i<=n;i++){id[i]=did[i]=i;}

	for(int i=1;i<=st;i++){
		for(int j=0;j<sw[i].size();j++){
			int x=sw[i][j].first,y=sw[i][j].second,u,v;

			swap(did[x],did[y]);
			swap(id[did[x]],id[did[y]]);
			u=s[did[x]],v=s[did[y]];
			s[did[x]]=v,s[did[y]]=u;	// 完全没用的调试信息
		}
		
		int l=1;	// 运用反复的修辞手法
		for(int j=1;j<=n;j++){
			if(s[j]==1){
				l=j+1;
			}
			if(s[l]==0 && s[j]==0){ans=max(ans,j-l+1);}
		}
		
	}

	printf("%d\n",ans);

	return 0;
}