自动搬运

查看原文

来自洛谷，原作者为

	Reaepita **

搬运于2025-08-24 21:59:36，当前版本为作者最后更新于2020-03-03 21:02:34，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

若公式失效请到博客内查看

若公式失效请到博客内查看

若公式失效请到博客内查看

为了防止有人看不见（重复三遍）

题上要求我们求出：选择一对 $i,j,i+1<j$ 将序列分为三段（$[1,i],[i+1,j-1],[j,n]$）至少有一段包含子串 $S_{l,r}$ 的方案。

直接求没有什么思路，考虑求出每一段都不包含子串 $S_{l,r}$ 的方案，然后用总方案 ${n-1}\choose 2$ 减掉即可。

由于题上要求 $l,r$ 不相邻所以总方案是 ${n-1}\choose 2$ 。

---

首先要知道所有与 $S_{l,r}$ 相同的子串的位置。

这个可以直接用后缀自动机+线段树合并+树上倍增求出

现在我们就得到了每个与 $S_{l,r}$ 相同的子串的位置，假设有 $m$ 个这样的子串，第 $i$ 个子串位于 $[l_i,r_i]$ 。

首先可以观察得出如果存在三个以上互不相交的子串，答案为 $0$。

那么剩下的子串只存在两种情况。

下文出现的 $len$ 指询问的子串长度。

情况 1

最靠左的子串与最靠右的子串相交

在这里我们将 $i$ 选择的位置分类。

1. 当 $i\in[1,l_1)$ 时，显然 $S_{1,i}$ 不包含任何子串，那么只需要保证 $S_{i+1,j-1}$ 和 $S_{j,n}$ 不包含任意子串即可。可以发现合法的 $j$ 选择的区间一定是 $(l_m,r_1]$。

   这部分的贡献为：

   $$(l_1-1)(r_1-l_m)$$

2. 当 $i\in[l_i,l_{i+1})$ 时，显然 $S_{1,i}$ 不包含任何子串，此时 $S_{j,n}$ 的限制就是 $l_m<j$ ， $S_{i+1,j-1}$ 的限制是 $j\leq r_{i+1}$。（如上图所示，当 $i\in[l_1,l_2)$ 时 $j\in(l_3,r_2]$ ，当 $i\in[l_2,l_3)$ 时 $j\in(l_3,r_3]$）

   这类情况贡献为：

   $$\sum_{i=1}^{m-1}(l_{i+1}-l_i)(r_{i+1}-l_m)=\sum_{i=1}^{m-1}(r_{i+1}-r_i)(r_{i+1}-l_m) $$

3. 当 $i\in[l_m,r_1)$ 时，只需要保证 $i+1<j$ 即可，此时的方案数相当于 $j$ 在 $[l_m,r_1]$ 中的方案数$+\ j$ 在 $(r_1,n]$ 中的方案数。

   这部分的贡献为：

   $${{r_1-l_m}\choose 2}+(r_1-l_m)(n-r_1)$$

4. 当 $i\in[r_1,n]$ 时，答案为 $0$

所以情况 $1$ 的总方案是

$$\sum_{i=1}^{m-1}(r_{i+1}-r_i)(r_{i+1}-l_m)+{{r_1-l_m}\choose 2}+(r_1-l_m)(n-r_1)+(l_1-1)(r_1-l_m) $$

情况 2

最靠左的子串与最靠右的子串不相交

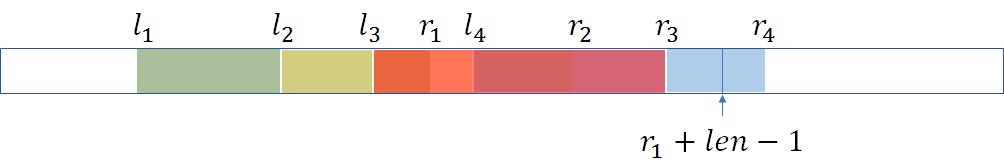
对于这种情况，可以发现满足条件的 $i,j$ 首先必须满足 $i<r_1,l_m<j$ 。

1. 由于最靠左的区间和最靠右的区间并不相交，所以如果 $i\in[1,l_1)$ 显然不存在合法的 $j$ 。

2. 当 $i\in[l_i,l_{i+1})$ 时，可以发现这里与情况 $1$ 唯一不同点就在于 $l_{i+1}$ 可能大于 $r_1$ （$l_4>r_1$）。

   可以观察的出，若 $l_m<r_{i+1}$ 且 $l_{i+1}<r_1$ 还是可以使用情况 $1$ 的方法求出即：

   $$\sum_{i=1}^{m-1}(r_{i+1}-r_i)(r_{i+1}-l_m),l_m<r_{i+1}<r_1+len-1 $$

   如上图所示此时我们已经求出了 $i\in[l_1,l_3)$ 的答案，但是当 $i\in[l_3,r_1)$ 中的答案在上式中并没有被计算。

   这种情况贡献显然是 $(r_1-l_3)(r_4-l_4)$

   更普遍的，找到 $r_1+len-1$ 的在 right 集合中的前驱 $p_1$ 和后继 $p_2$

   那这种情况的贡献为 $(r_1-l_{p_1})(r_{p_2}-l_m),r_{p_2}>l_m$

所以情况 $2$ 比情况 $1$ 复杂许多。

但本质只有两个求和公式

$$\sum_{i=1}^{m-1}(r_{i+1}-r_i)(r_{i+1}-l_m),l_m<r_{i+1}<r_1+len-1 $$$$(r_1-l_{p_1})(r_{p_2}-l_m),r_{p_2}>l_m$$

代码实现

线段树需要维护区间最大值，区间最小值，还需要维护 $(r_{i+1}-r_i)r_{i+1}$ 和 $(r_{i+1}-r_i)$。

对于一个询问 $l,r$

通过倍增找到 $S_{1,r}$ 对应 parent 树上哪个节点。

然后先判断是否存在三个不相交的区间，可以先找出最靠左的位置和最靠右的位置然后查询区间最大值。

然后对于情况 $1$ 或情况 $2$ 分别求解。

可以发现情况 $1$ 和情况 $2$ 都有 $(r_{i+1}-r_i)(r_{i+1}-l_m)=(r_{i+1}-r_i)r_{i+1}-(r_{i+1}-r_i)l_m$ 。

#include<bits/stdc++.h>
using namespace std;
const int maxn=2e5+10;
const int inf=0x3f3f3f3f;
struct Node{int Min,Max;long long sum1,sum2;}tr[maxn*40];
struct Segment_Tree
{
    int son[maxn*40][2],tot;
    Node merge(const Node &a,const Node &b)
    {
        Node c;
        c.Min=min(a.Min,b.Min);
        c.Max=max(a.Max,b.Max);
        c.sum1=a.sum1+b.sum1+b.Min*1LL*(b.Min-a.Max);
        c.sum2=a.sum2+b.sum2+b.Min-a.Max;
        return c;
    }
    int Find_Max(int l,int r,int rt,int L,int R)
    {
        if(!rt)return 0;
        if(L<=l&&r<=R)return tr[rt].Max;
        int mid=l+r>>1,ans=0;
        if(L<=mid)ans=Find_Max(l,mid,son[rt][0],L,R);
        if(R>mid)ans=max(ans,Find_Max(mid+1,r,son[rt][1],L,R));
        return ans;
    }
    int Find_Min(int l,int r,int rt,int L,int R)
    {
        if(!rt)return inf;
        if(L<=l&&r<=R)return tr[rt].Min;
        int mid=l+r>>1,ans=inf;
        if(L<=mid)ans=Find_Min(l,mid,son[rt][0],L,R);
        if(R>mid)ans=min(ans,Find_Min(mid+1,r,son[rt][1],L,R));
        return ans;
    }
    Node tmp;
    void Query(int l,int r,int rt,int L,int R)
    {
        if(!rt)return;
        if(L<=l&&r<=R)
        {
            if(tmp.Min==0)tmp=tr[rt];
            else tmp=merge(tmp,tr[rt]);
            return ;
        }
        int mid=l+r>>1;
        if(L<=mid)Query(l,mid,son[rt][0],L,R);
        if(R>mid)Query(mid+1,r,son[rt][1],L,R);
    }
    void update(int l,int r,int &rt,int p)
    {
        if(!rt)rt=++tot;
        if(l==r)
        {
            tr[rt].Min=tr[rt].Max=p;
            tr[rt].sum1=tr[rt].sum2=0;
            return;
        }
        int mid=l+r>>1;
        if(p<=mid)update(l,mid,son[rt][0],p);
        else update(mid+1,r,son[rt][1],p);
        if(son[rt][0]&&son[rt][1])tr[rt]=merge(tr[son[rt][0]],tr[son[rt][1]]);
        else if(son[rt][0])tr[rt]=tr[son[rt][0]];
        else tr[rt]=tr[son[rt][1]];
    }
    int Merge(int x,int y)
    {
        if(!x||!y)return x+y;
        int rt=++tot;
        son[rt][0]=Merge(son[x][0],son[y][0]);
        son[rt][1]=Merge(son[x][1],son[y][1]);
        if(son[rt][0]&&son[rt][1])tr[rt]=merge(tr[son[rt][0]],tr[son[rt][1]]);
        else if(son[rt][0])tr[rt]=tr[son[rt][0]];
        else tr[rt]=tr[son[rt][1]];
        return rt;
    }
}T;
int root[maxn],cnt=0,lst;
int son[maxn][10],fa[maxn];
int len[maxn],pos[maxn],up[maxn][19],dep[maxn];
void Add(int c,int id)
{
    int cur=++cnt,p=lst;
    lst=pos[id]=cur,len[cur]=len[p]+1;
    while(p&&!son[p][c])son[p][c]=cur,p=fa[p];
    if(!p)fa[cur]=1;
    else 
    {
        int q=son[p][c];
        if(len[p]+1==len[q])fa[cur]=q;
        else 
        {
            int nq=++cnt;len[nq]=len[p]+1;
            memcpy(son[nq],son[q],sizeof(son[q]));
            fa[nq]=fa[q],fa[q]=fa[cur]=nq;
            while(p&&son[p][c]==q)son[p][c]=nq,p=fa[p];
        }    
    }    
}
int n;
int head[maxn],ecnt=0;
struct edge{int v,nxt;}e[maxn<<1];
void add(int u,int v){e[++ecnt]=(edge){v,head[u]},head[u]=ecnt;}
void dfs(int u)
{
    up[u][0]=fa[u];
    for(int i=1;i<=18;i++)up[u][i]=up[up[u][i-1]][i-1];
    for(int i=head[u];~i;i=e[i].nxt)
    {
        int v=e[i].v;
        dep[v]=dep[u]+1;
        dfs(v);
        if(u!=1)root[u]=T.Merge(root[u],root[v]);
    }
}
void build()
{
    memset(head,-1,sizeof(head)),ecnt=0;
    for(int i=1;i<=cnt;i++)if(fa[i])add(fa[i],i);
    for(int i=1;i<=n;i++)T.update(1,n,root[pos[i]],i);
    dfs(1);
}
long long C(int len)
{
    if(len<2)return 0;
    return len*1LL*(len-1)/2;
}
long long query(int l,int r)
{
    int Len=r-l+1,u=pos[r];
    for(int i=18;i>=0;i--)if(len[up[u][i]]>=Len)u=up[u][i];
    int L=tr[root[u]].Min,R=tr[root[u]].Max;
    if(L<R-Len*2+1&&T.Find_Max(1,n,root[u],L,R-Len)-Len+1>L)return C(n-1);
    if(R-Len+1<=L)
    {
        Node now=tr[root[u]];
        int lm=R-Len+1;
        long long ans=now.sum1-now.sum2*lm+C(L-lm)+(L-lm)*1LL*(n-Len);
        return C(n-1)-ans;
    }
    else 
    {
        T.tmp=(Node){0,0,0,0};
        int lm=R-Len+1,poslm=T.Find_Max(1,n,root[u],1,lm);
        T.Query(1,n,root[u],poslm,L+Len-1);
        Node now=T.tmp;
        int p1=T.Find_Max(1,n,root[u],1,L+Len-1);
        int p2=T.Find_Min(1,n,root[u],L+Len,n);
        long long ans=now.sum1-now.sum2*lm+(p2>lm?(L-(p1-Len+1))*1LL*(p2-lm):0);
        return C(n-1)-ans;
    }
}
char s[maxn];
int q;
int main()
{
    scanf("%d%d",&n,&q);
    scanf("%s",s+1);
    cnt=lst=1;
    for(int i=1;i<=n;i++)Add(s[i]-'0',i);
    build();
    while(q--)
    {
        int l,r;
        scanf("%d%d",&l,&r);
        printf("%lld\n",query(l,r));
    }
}