自动搬运

查看原文

来自洛谷，原作者为

	shadowice1984 これが勘違いでも、これが勘違いでも

搬运于2025-08-24 21:59:07，当前版本为作者最后更新于2018-11-28 17:47:15，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

stO jry Orz

这题真的是神仙题,爆肝了160行调了一天半才淦出来，可能是我太菜了吧……

顺便说一句jyy的题解里面的式子就没几个系数是对的所以写篇题解至少把题解里的式子修正了

---

本题题解

首先我们需要通过观察获得一些性质

我们在线图变化的时候将每个点标上一些号，然后重新考虑一下题目中给出的变换的本质是什么

让我们来手玩一下一个6个点的树的前3阶线图(第4阶时候点就要开始爆炸了实在画不动)

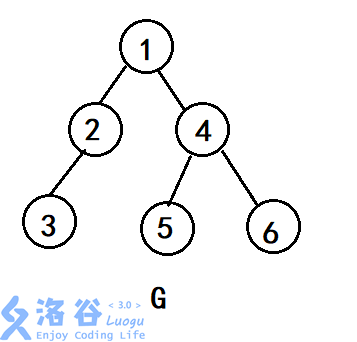
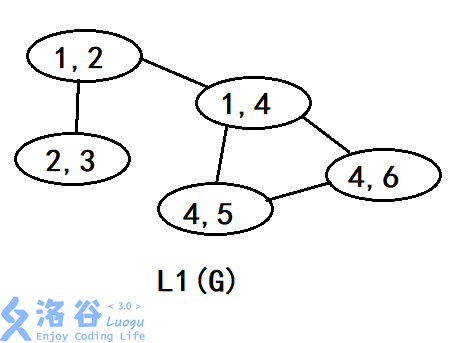
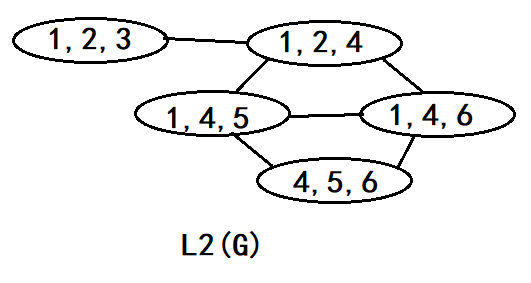
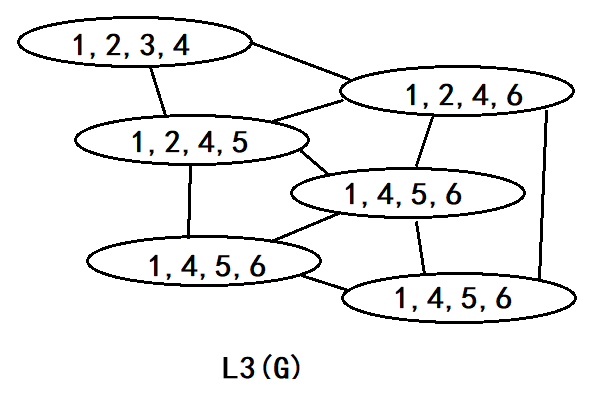
凝视一下这四张图，除了发现点数越来越多以及图越来越乱之外你还发现了什么？

这里为了方便你发现问题的本质每个点的编号并没有重新编号而是使用原图的点对线图中的点进行编号

我们发现到$L3(G)$的时候有3个点的编号全部相同都是$1,4,5,6$为什么呢？

看一眼原图当中$1,4,5,6$这个联通块，手玩下它的三阶线图，你会发现一件事就是这个联通块的3阶线图当中恰好有3个点的标号是$1,4,5,6$

同理$1,2,3,4$这个的联通块的3阶线图只有1个点的标号对应了$1,2,3,4$

同理我们手玩了$1,2,4,5$和$1,2,4,6$之后也能得到相同的结论

这个神奇的标号对应着什么呢？

似乎刚好是原图当中一个大小为$k+1$的联通块

但是这个结论似乎有些不对，考虑一个3元环的无限阶线图还是个3元环，因此我们可以得出一个结论是我们给点的标号对应的点集其实是原图当中一个大小不超过k+1个点的联通块

那么我们还能得出一个结论是原图当中一个大小不超过$k+1$的联通块在做k次线图变换之后会对应着线图当中的x个点，x为这个联通块做k次线图变化之后标号中的数字个数为k+1的点的数目

那么我们有了一个初步的暴力就是枚举原图中所有联通块然后考虑这些联通块对答案的贡献

似乎k=1,2,3的时候联通块的种类不会特别多？

你看k=1的时候合法点联通块就一种，一条边,这东西对答案贡献是1

k=2的时候合法的连通块就一种，一个两条边构成的链,对答案贡献是1

k=3的时候合法的联通块有两种,一种是3条边构成的链，对答案贡献是1

另一种是形如我们之前手玩的$1,4,5,6$这样的三叉形状，对答案的贡献是3，

还有一种是3元环，对答案的贡献是3

所以根据这个我们可以列出k=1,2,3的时候答案的式子，设有n个点m条边

你会发现k=3的时候吉老师题解中的式子是假的

$$ans=n-1$$ $$ans=\sum_{i=1}^{n}{d_{i}\choose 2}$$ $$ans=\sum_{i=1}^{m}(d(u_{i})-1)(d(v_{i})-1)+\sum_{i=1}^{n}3{d_{i}\choose 3} $$

好了让我们再来考虑另一个辣手的情况，能不能凭借人类的智慧算出$k=4$时的答案呢？

答案是可行的，我们把$L^{4}(G)$转化成$L^{3}(L(G))$~~(这里吉老师题解里的式子又错了)~~来算

首先我们可以将每个边在$L(G)$中的度数算出来,设这东西是$d1(u,v)$则显然有

$$d1(u,v)=d(u)+d(v)-2$$

(这里吉老师题解里的式子双错了)

然后我们接下来算出每个点周围一圈边在$L(G)$当中的度数之和，为了方便起见我们令

$$d2(u)=\sum_{v \in alist(u)}d1(u,v)-1$$

(其中alist(u)是u的出边集合)

那么我们接下来考虑k=3时候每一个$(d(u)-1)(d(v)-1)$对答案的贡献我们可以推出来这样一个式子

$$0.5\sum_{i=1}^{n}d2(i)^2-\sum_{i=1}^{m}(d1(u_{i},v_{i})-1)^2+\sum_{i=1}^{m}3{d1(u_{i},v_{i}) \choose 3} $$

之所以前面的平方要乘0.5是因为每个交叉项被算了两边并且每条边自己的平方也在两个点处各被算了一遍，然后后面的式子减去了每个边自己的平方

然后这东西就是$k=4$时候的答案式子了

好了我们现在借助人类智慧手玩完了$k=1,2,3,4$时候的答案了

现在让我们来考虑k=9的鬼畜数据

我们的思想依然不变，考虑每个联通块对答案的贡献

不过显然$2^n$暴力枚举联通块显然t飞了

那么我们发现一个一个相当重要的信息，两个联通块如果图同构，那么这两个联通块对答案的贡献显然相同

那么我们似乎可以枚举所有不同构并且点不超过$k+1$的有根树,然后计算每一种有根树对答案的贡献，这样似乎看起来可以很快的求出答案

且慢……你怎么枚举所有不同构的有根树啊

Part1 枚举不同构的有根树

首先我们发现树的点最多10个，因此可以大力dfs所有不同的树的欧拉序(有人也叫括号序列),复杂度显然是卡特兰数级别的，在$n=10$的时候可以轻松的搜出来

当我们dfs出来一个树之后，我们把它树哈希一下,然后判断这个hash值是否已经搜过了，如果已经搜过了我们就不枚举他

注意一件事是树hash的函数搞的越乱越好，一开始疯狂撞hash……

如果不会树hash的话可以自己yy/看我代码/去你站模板区/自行百度

---

好了我们兴奋的打了个搜索上去，发现一件事情，合法的树出乎意料的少，只有$1205$种(你可以用这个数字检验一下你的dfs有没有写错)

因此似乎枚举每一种树对答案的贡献是可行的

那么我们知道一个联通块对答案的贡献是它做k次线图变换之后对应着自身的点的数目

那么我们怎么对这$1205$种树都求出它对答案的贡献呢？

假设我们想要求树T对答案的贡献，设他是$w(T)$

Part2 求解w(T)

其实我们思路暴力的很，假设我们所有的树T是按照点数进行枚举的话，我们可以求出这个图的k阶线图中有几个点，然后把这个树中子图的$w$之和算出来然后减掉就能求出$w(T)$了

然后我们发现算所有子图的$w$之和实在是很容易，因为任意一个子图的点数肯定小于$T$的点数，所以这个$w$值你之前算过，我们拿map存每一个hash值对应的w值即可完成任务

因此现在的任务就落在了如何求出T的k阶线图当中的点数

这个东西的思路更加暴力，$L^9(G)=L^4(L^5(G))$

所以直接硬算出5阶线图，然后去套4阶线图的公式

注意一件事最坏情况下5阶线图大概会有几百万条边(我的邻接表直接开了1e7)，但是这样的树非常少，因此总的复杂度可以接受

然后给你求线图的过程当中加点特技实现个$O(m)$求线图，你就能在时限内跑出来了，具体细节可以看我代码里的line_gr::getline()

(吉老师std真的是可怕,9阶线图居然只有600多毫)

---

好了千辛万苦我们终于把每种树对答案的贡献求出来了，现在我们只需要dp出每种树在大的树当中出现了多少次就可以算出答案了，假设这个数$T$在大树当中出现了$time(T)$次，那么我们该怎么求解答案呢？

part3 求解time(T)

依然是更加暴力的思路，我们采用状压dp来实现这个东西的求解

我们设$dp(i,j)$表示$i$的子树当中匹配小树当中$j$的子树有多少种方案

那么转移似乎需要使用一个状压的辅助数组来帮助我们合并一条父子边$(u,v)$

这样直接大力转移似乎复杂度最满的时候是$O(2^k)$的，可能我们需要卡卡常数卡到$O(2^{0.5k})$

当我们转移$j$的时候先忽略到和$j$相连的所有叶子，然后此时假设我们的点j还剩下$p$个剩下的子树，然后和$j$相连的叶子一共有$lf$个，当前的i有$son$个儿子

那么我们dp之后应该要把答案乘上${son-p \choose lf}lf!$才能保证我们的答案是对的？

显然不对，因为你重复计数了

这里不是因为我们多乘了一个lf的阶乘，而是因为另外一个原因

考虑一个长这样的树

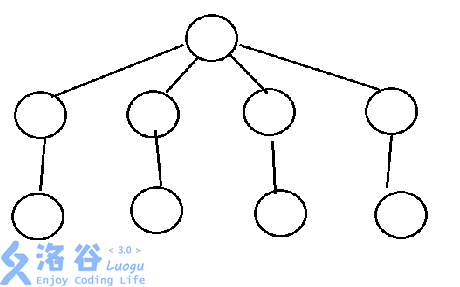
我们在dp根节点的时候并不会删掉任何的叶子，然而我们发现答案比真实答案大24倍，为什么呢？

因为根节点的所有子树完全同构……但是我们dp的时候强行认为每个子树都不同构，这样的话同一个方案会被重复的计算24次也就是4!次

所以我们在每一次转移之后都要把$dp(i,j)$除上这个式子

$$\prod_{i}cnt_{i}!$$

其中$cnt_{i}$表示子树中第$i$种$hash$值的出现次数，这个东西可以在树hash的时候顺手求出来

这就是为什么我们在丢掉叶子的时候乘上一个阶乘的原因了，因为我们需要把这两个系数抵消掉(不然我们的系数算起来会炒鸡恶心)

当然只要你足够聚这题还有很多的去重方式可以用

然后我们一通树形dp之后我们就求出了time(T)了

然后我们就做完了这题……

上代码~(这题真的很肝……)

#include<cstdio>
#include<algorithm>
#include<queue>
#include<map>
#include<set>
using namespace std;const int N=5010+10;const int E=1e7+10;const int M=13;typedef long long ll;
typedef unsigned long long ull;ll fac[N];
const ll mod=998244353;const ll bas=467;set <ull> book;int psiz[12];
inline ll po(ll a,ll p){ll r=1;for(;p;p>>=1,a=a*a%mod)if(p&1)r=r*a%mod;return r;}
ull tr[15];int hd;ll ch[N][25];ll xs[15];int lb[N];int siz[N];int k;ll ans;int n;
# define ctwo(x) ((((ll)x*(x-1))>>1)%mod)
# define ctre(x) ((ll)x*(x-1)%mod*(x-2)%mod*499122177%mod)
struct tree1
{
	int gr[15];ull nhsh[15];int siz[15];int rot;int vis;
	inline int& operator [](const int& x){return gr[x];}
	inline void ins(int u,int v){gr[u]|=(1<<v);}
	inline void clr(){for(int i=0;i<13;i++)gr[i]=0;}
	inline void pre(int u)//处理hash值 
	{
		siz[u]=1;for(int t=gr[u];t;t-=t&(-t))pre(lb[t]),siz[u]+=siz[lb[t]];
		hd=0;for(int t=gr[u];t;t-=t&(-t))tr[++hd]=nhsh[lb[t]];
		nhsh[u]=0;sort(tr+1,tr+hd+1);xs[u]=1;
		ull mi=1;for(int i=1;i<=hd;i++,mi=mi*bas)nhsh[u]+=mi*tr[i];
		int fac=1;for(int i=1,cnt=0;i<=hd;i++)
			if(tr[i]==tr[i-1])cnt++,fac*=cnt;else xs[u]*=fac,cnt=1,fac=1;
		nhsh[u]=(siz[u]!=1)?7+nhsh[u]*siz[u]:13;
		xs[u]=po(xs[u]*fac,mod-2);
	}
	inline void cst(int u,const int& lim)//求出一个联通块的hash 
	{
		vis|=(1<<u);psiz[u]=1;
		for(int t=gr[u]&lim;t;t-=t&(-t))cst(lb[t],lim),psiz[u]+=psiz[lb[t]];
		hd=0;for(int t=gr[u]&lim;t;t-=t&(-t))tr[++hd]=nhsh[lb[t]];
		nhsh[u]=0;sort(tr+1,tr+hd+1);
		ull mi=1;for(int i=1;i<=hd;i++,mi=mi*bas)nhsh[u]+=(ll)mi*tr[i];
		nhsh[u]=(psiz[u]!=1)?7+nhsh[u]*psiz[u]:13;
	}
	inline int ck(const int& lim)//检查联通性 
	{
		int mx=lb[lim&(-lim)];
		for(int i=0;i<=12;i++)if((lim>>i)&1)mx=siz[mx]<siz[i]?i:mx;
		vis=0;cst(mx,lim);return (vis==lim)?mx:-1;
	}
}ntr,sub;
namespace line_gr
{
	int al[2][E];int x[2][E];int ct[2];int v[2][E];int d1[E];int d2[E];map <ull,int> mp;
	inline void spadd(int u,int V){v[0][++ct[0]]=V,x[0][ct[0]]=al[0][u],al[0][u]=ct[0];}
	inline void get_line(int* v1,int* x1,int* al1,int ct1,
	int* v,int* x,int* al,int& ct)//从一个图迭代到它的线图 
	{
		for(int i=1;i<=ct+1;i++)al[i]=0;ct=0;
		for(int i=2;i<=ct1;i+=2)
		{
			int tu=v1[i];int tv=v1[i-1];int p=i>>1;
			for(int j=al1[tu],q=(j+1)>>1;j;j=x1[j],q=(j+1)>>1)
				if(q<p)v[++ct]=q,x[ct]=al[p],al[p]=ct,v[++ct]=p,x[ct]=al[q],al[q]=ct;
			for(int j=al1[tv],q=(j+1)>>1;j;j=x1[j],q=(j+1)>>1)
				if(q<p)v[++ct]=q,x[ct]=al[p],al[p]=ct,v[++ct]=p,x[ct]=al[q],al[q]=ct;
		}
	}
	inline ll calcline4(int* v,int ct)//求4阶线图 
	{
		ll ret=0;for(int i=1;i<=ct;i++)d1[v[i]]++;
		for(int i=2;i<=ct;i+=2)d2[i>>1]=d1[v[i]]+d1[v[i-1]]-2;
		for(int i=1;i<=(ct>>1);i++)(ret+=ctre(d2[i])*2)%=mod;
		for(int i=1;i<=(ct>>1);i++)d2[i]--;
		for(int i=1;i<=ct+1;i++)d1[i]=0;
		for(int i=1;i<=ct;i++)d1[v[i]]+=d2[(i+1)>>1];
		for(int i=1;i<=ct+1;i++)(ret+=(ll)d1[i]*d1[i])%=mod;
		(ret*=499122177)%=mod;
		for(int i=1;i<=(ct>>1);i++)(ret+=mod-(ll)d2[i]*d2[i]%mod)%=mod;
		for(int i=1;i<=ct+1;i++)d1[i]=0;for(int i=1;i<=ct;i++)d2[i]=0;return ret;
	}
	inline ll subcalc(tree1& ter,int tt)//求一个图的k阶线图 
	{
		for(int i=1;i<=ct[0]+1;i++)al[0][i]=0;ct[0]=0;
		for(int i=0;i<tt;i++)	
			for(int t=ter[i];t;t-=t&(-t))
			{spadd(i+1,lb[t]+1),spadd(lb[t]+1,i+1);}
		for(int i=1,p=1,q=0;i<=k-4;i++,p^=1,q^=1)
			get_line(v[q],x[q],al[q],ct[q],v[p],x[p],al[p],ct[p]);
		return calcline4(v[(k-4)&1],ct[(k-4)&1]);	
	}
	inline ll calcw(tree1& ter)//容斥 
	{
		int tt=ter.siz[ter.rot];ll ret=subcalc(ter,tt);sub=ter;
		for(int i=1;i<(1<<tt)-1;i++)
			{sub.rot=sub.ck(i);if(sub.rot==-1)continue;(ret+=mod-mp[sub.nhsh[sub.rot]])%=mod;}
		return mp[ter.nhsh[0]]=ret;
	}
}
int v[2*N];int x[2*N];int ct;int al[N];ll dp[N][12];ll tdp[N];int d[N];int lf[N];
int st[N];int tp;int eu[N];
inline void add(int u,int V){v[++ct]=V;x[ct]=al[u];al[u]=ct;d[V]++;}
inline void dfs(int u,int f)//树形dp 
{
	int son=0;for(int i=al[u];i;i=x[i])if(v[i]!=f)dfs(v[i],u),son++;
	for(int rt=0;rt<ntr.siz[0];rt++)//去重 
	{
		if(ntr.siz[rt]==1)continue;if(son<siz[sub[rt]]){dp[u][rt]=0;continue;}
		for(int k=sub[rt];k;k=(k-1)&sub[rt])tdp[k]=0;tdp[0]=1;
		for(int i=al[u];i;i=x[i])
		{
			if(v[i]==f)continue;
			for(int k=sub[rt];k;k=(k-1)&sub[rt])
				for(int p=k,lob;p;p-=lob)lob=p&(-p),(tdp[k]+=tdp[k^lob]*dp[v[i]][lb[p]])%=mod;
		}dp[u][rt]=tdp[sub[rt]]*xs[rt]%mod*ch[son-siz[sub[rt]]][lf[rt]]%mod;
	}
}
inline ll calct(const tree1& ter)//计算time 
{
	sub=ter;for(int i=0;i<sub.siz[0];i++)lf[i]=0;
	for(int i=0;i<sub.siz[0];i++)
		for(int p=sub[i];p;p-=p&(-p))
			if(sub.siz[lb[p]]==1)lf[i]++,sub[i]^=p&(-p);
	dfs(1,0);ll ans=0;for(int i=1;i<=n;i++)(ans+=dp[i][0])%=mod;return ans;
}
inline void solve(int hd,int cur,int sum,int tar)//搜出所有不同构的树 
{
	if(sum==0&&cur!=-1)
	{
		if(cur!=tar)return;tp=0;ntr.clr();
		for(int i=1;i<hd;i++)
			if(eu[i]>=0)st[++tp]=eu[i];else if(tp!=1)tp--,ntr.ins(st[tp],st[tp+1]);	
		ntr.rot=0;ntr.pre(0);
		if(book.count(ntr.nhsh[0])==0)
		{book.insert(ntr.nhsh[0]),(ans+=calct(ntr)*line_gr::calcw(ntr))%=mod;}return;
	}if(sum!=0){eu[hd]=-1;solve(hd+1,cur,sum-1,tar);}
	if(cur!=tar){eu[hd]=cur+1;solve(hd+1,cur+1,sum+1,tar);}
}
inline ll calcline2()//二阶线图 
{ll ans=0;for(int i=1;i<=n;i++)(ans+=ctwo(d[i]))%=mod;return ans;}
inline ll calcline3()//三阶线图 
{
	ll ans=0;for(int i=1;i<=n;i++)(ans+=ctre(d[i]))%=mod;
	for(int i=2;i<=ct;i+=2)(ans+=(ll)(d[v[i]]-1)*(d[v[i-1]]-1))%=mod;return ans;
}
int main()
{
	for(int i=0;i<=11;i++)lb[1<<i]=i;
	for(int i=1;i<2048;i++)lb[i]=lb[i&(-i)];
	for(int i=1;i<2048;i++)siz[i]=siz[i>>1]+(i&1);
	for(int i=0;i<=5000;i++)
	{
		ch[i][0]=1;if(i<=20)ch[i][i]=1;
		for(int j=1;j<=min(i-1,20);j++)ch[i][j]=(ch[i-1][j-1]+ch[i-1][j])%mod;
	}fac[0]=1;for(int i=1;i<=20;i++)fac[i]=fac[i-1]*i%mod;
	for(int i=0;i<=5000;i++)for(int j=0;j<=20;j++)(ch[i][j]*=fac[j])%=mod;
	scanf("%d%d",&n,&k);
	for(int i=1,u,V;i<n;i++)scanf("%d%d",&u,&V),add(u,V),add(V,u);
	switch(k)//1,2,3,4大力算然后剩下的搜 
	{
		case 1:{printf("%d",n-1);break;}
		case 2:{printf("%lld",calcline2());break;}
		case 3:{printf("%lld",calcline3());break;}
		case 4:{printf("%lld",line_gr::calcline4(v,ct));break;}
		default:{for(int i=0;i<=k;i++)solve(1,-1,0,i);printf("%lld",ans);break;}
	}return 0;//再见这道毒瘤题…… 
}