自动搬运

查看原文

来自洛谷，原作者为

	中国飞鱼 **

搬运于2025-08-24 21:58:57，当前版本为作者最后更新于2018-07-30 22:45:33，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

大家观察一张图

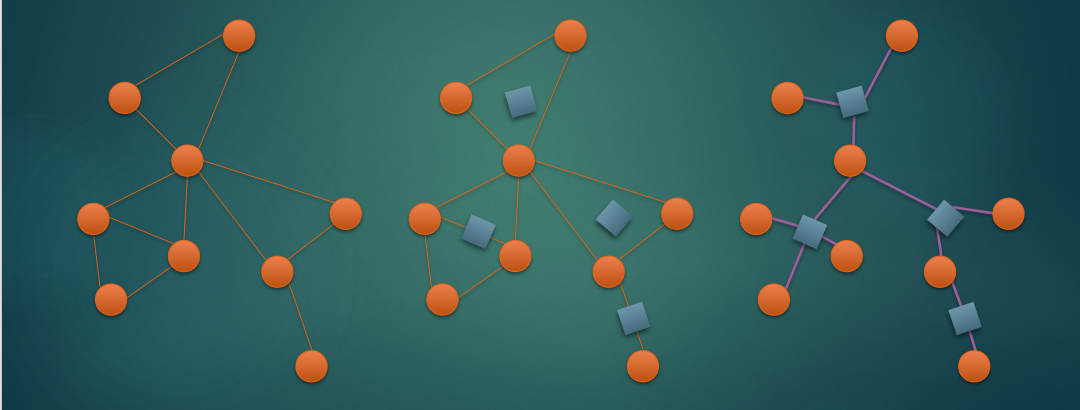
有什么发现?

必经点数==圆方树上两点路径上圆点数

也就等于边数/2+1

于是对图建出广义圆方树(怎么建?$tarjan$求点双,在一个点双里的向一个新建的方点连边即可)

然后树剖求$lca$,答案就是$(dep[u]+dep[v]-2*dep[lca])/2+1$

亲测树剖时间是倍增一半

#define il inline
#define ri register int
#include<iostream>
using namespace std;
const int N=1e6+5,M=4e6+5;
il int re(){
    ri x=0,w=1;register char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
    while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
    return x*w;
}
int n,E,m,ts,tp,tot;
int dfn[N],low[N],st[N],dep[N],top[N],sz[N],son[N],fa[N];
struct Graph{
    int cnt,last[N],nxt[M],to[M];
    il void link(ri u,ri v){
        nxt[++cnt]=last[u];to[cnt]=v;last[u]=cnt;
        nxt[++cnt]=last[v];to[cnt]=u;last[v]=cnt;
    }
}G,T;
void tarjan(ri u){
    dfn[u]=low[u]=++ts;st[++tp]=u;
    for(ri i=G.last[u],v;i;i=G.nxt[i]){
        v=G.to[i];
        if(!dfn[v]){
            tarjan(v);
            low[u]=min(low[u],low[v]);
            if(low[v]>=dfn[u]){
                T.link(++tot,u);
                ri x=0;
                do{
                    x=st[tp--];T.link(tot,x);
                }while(x!=v);
            }
        }
        else low[u]=min(low[u],dfn[v]);
    }
}
void dfs1(ri u){
    sz[u]=1;
    for(ri i=T.last[u],v;i;i=T.nxt[i]){
        v=T.to[i];
        if(v==fa[u])continue;
        dep[v]=dep[u]+1;
        fa[v]=u;
        dfs1(v);
        sz[u]+=sz[v];
        if(sz[v]>sz[son[u]])son[u]=v;
    }
}
void dfs2(ri u,ri Tp){
    top[u]=Tp;
    if(son[u])dfs2(son[u],Tp);
    for(ri i=T.last[u],v;i;i=T.nxt[i]){
        v=T.to[i];
        if(v==son[u]||v==fa[u])continue;
        dfs2(v,v);
    }
}
il int Query(ri x,ri y){
    while(top[x]!=top[y]){
        if(dep[top[x]]<dep[top[y]])swap(x,y);
        x=fa[top[x]];
    }
    return dep[x]<dep[y]?x:y;
}
int main(){
    tot=n=re(),E=re();
    for(ri i=1,u,v;i<=E;i++){
        u=re(),v=re();
        G.link(u,v);
    }
    tarjan(1);
    dep[1]=1;dfs1(1);dfs2(1,1);
    m=re();
    ri u,v,lca;
    while(m--){
        u=re(),v=re();
        lca=Query(u,v);
        printf("%d\n",(dep[u]+dep[v]-2*dep[lca])/2+1);
    }
    return 0;
}