自动搬运

查看原文

来自洛谷，原作者为

	小粉兔 Always continue; Never break;

搬运于2025-08-24 21:58:42，当前版本为作者最后更新于2020-01-28 22:16:43，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

在博客园食用更佳：https://www.cnblogs.com/PinkRabbit/p/12238880.html。

题意简述：

给定一个 $n$ 个点，$m$ 条边的简单有向无环图（DAG），求出它的最长反链，并构造方案。

最长反链：一张有向无环图的最长反链为一个集合 $S \subseteq V$，满足对于 $S$ 中的任意两个不同的点 $u, v \in S$（$u \ne v$），$u$ 不能到达 $v$，$v$ 也不能到达 $u$，且 $S$ 的大小尽量大。

题解：

根据 Dilworth 定理，一个 DAG 中最长反链的大小，等于其最小链划分的大小。

最小链划分：在 DAG 中选出若干条链，每个点恰好属于其中一条链，且链数尽量少。
（这里的“链”可能与传统理解不同，请看下面的注释。）

需要注意的是，这里对“链”的定义，不需要是 DAG 中连续的一条链，只需要前一个点能通过路径到达后一个点即可。你也可以理解为：一条连续的链，挖掉中间的一些点，形成的点集也算作“链”。

另一个理解方式是：这里的“链划分”要求每个点不重不漏地属于一条链；但也可以理解为，链一定要是连续的，并且允许多条链重复经过同一个点，只需要保证每个点都被经过即可。（以这种角度去理解，可以称之为最小“可重链覆盖”。）

这两种理解方式（即 (1) 最小链划分 和 (2) 最小可重链覆盖）是等价的，只不过前者的链可以跳过中间的点。

在后文中，给出一种使用二分图匹配求 DAG 中的最小不可重链覆盖的方法。为了别求错，我们需要先对 DAG 求一次传递闭包，把 $u$ 能间接到达 $v$ 的点对之间的边 $u \to v$ 建出来，这样就把“可重链覆盖”转化为“不可重链覆盖”了。

注释：Dilworth 定理原本的描述是对于偏序集来说的。你可以将偏序集理解为“求过传递闭包的 DAG”，于是“可重”或“不可重”就无所谓了。

在这里大费周章地解释，就是为了提醒各位，求最长反链的时候，不要忘记对 DAG 求传递闭包。

这里给出使用二分图匹配求最小不可重链覆盖的方法。

考虑从每个点自成一条链的形态出发，此时恰好有 $n$ 条链。
可以发现最终答案一定是合并（首尾相接）若干条链形成的。考虑重新描述这个过程：
对于一个点，它在最终的链上，一定只有最多一个前驱，和最多一个后继。
我们考虑把每个点拆成入点和出点，那么入点和出点应该只能匹配上最多一个点（表示前驱或者后继）。

这似乎是二分图匹配的形式，具体地，我们考虑：
把一个点 $x$ 拆成两个点：$x_{out}$ 和 $x_{in}$，表示出点和入点。
对于一条边 $x \to y$，连接 $x_{out}$ 与 $y_{in}$，表示原图中 $x$ 的出边指向 $y$（这条边是 $y$ 的入边）。
那么最终形成了一个二分图，左侧是所有 $x_{out}$，右侧是所有 $x_{in}$。而且所有边都是连接左侧的点和右侧的点的。

在这个二分图 $G = \langle \langle V_{out}, V_{in} \rangle , E' \rangle$ 上做二分图最大匹配：
每一个匹配边 $x_{out} \leftrightarrow y_{in}$ 都可以还原原图中链的一条边 $x \to y$。
每匹配 $1$ 条边，链的个数就减少 $1$，则有最小链覆盖的大小等于 $n$ 减去最大匹配的大小。

继续考虑如何从二分图最大匹配中，构造出最长反链。以下部分参考了 r_64 的题解。

我们首先需要构造二分图最大独立集，这部分参考了「图的最大匹配算法」这篇博客：

考虑下图，可以求出它的其中一种最大匹配为 $\{ \langle 2, D \rangle, \langle 3, E \rangle, \langle 4, A \rangle, \langle 5, C \rangle \}$，设最大匹配大小为 $m$，这里 $m = 4$：

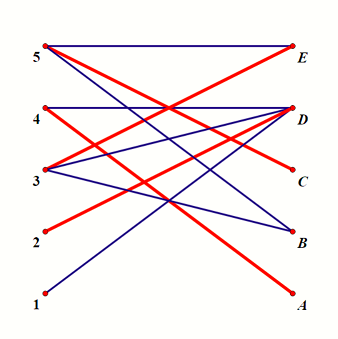
从右侧的非匹配点（这里为 $B$，可能有多个）开始 DFS，右侧的点只能走非匹配边向左访问，左侧的点只能走匹配边向右访问：

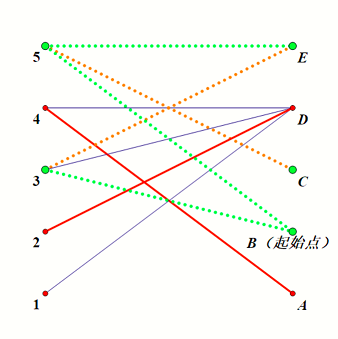
可以发现 DFS 到了 $3, 5, B, C, E$ 这些点。

我们取左侧被 DFS 到的点，以及右侧没被 DFS 到的点，也就是 $3, 5, A, D$ 这些点，记做集合 $S$，可以证明 $S$ 是一个最小点覆盖。
最小点覆盖：选取最少的点，覆盖每条边，也就是说每条边的两个端点至少有一个被选中了。

证明：

1. 首先有：最小点覆盖等于最大匹配。我们可以证明 $|S| = m$。
   这是因为：右侧的非匹配点一定都被 DFS 到了，所以在右侧选取的必然是匹配点。如果一个右侧的匹配点没被选取，即它被 DFS 到了，而这只有可能是因为它在左侧匹配到的点被 DFS 到了，那么左侧匹配到的点就会被选上。即是：每条匹配边的两端点恰好会被选一个。而左侧的非匹配点一定不会被 DFS 到，这是因为如果被 DFS 到了，必然会形成一条交错路（匈牙利算法中的），不满足最大匹配的条件。所以有且仅有匹配边的端点会被选上，而且每条匹配边的两端点恰好被选一个，所以 $\boldsymbol{|S| = m}$。

2. $S$ 可以覆盖所有的边。
   我们把边按照左右端点是否被 DFS 到，分成 $2 \times 2 = 4$ 类。那么如果出现了左端点没被 DFS 到，但是右端点被 DFS 到了的边，它才不会被覆盖。然而这是不可能的，这是因为对于一个右侧被 DFS 到的点，与它相连的左侧的点一定都被 DFS 到了。

然后有最大独立集等于最小点覆盖的补集。也就是只要选出左侧没被 DFS 到的点和右侧被 DFS 到的点就行了。
在上图中就是 $1, 2, 4, B, C, E$ 这 $6$ 个点。

回到 DAG 的情况（注意到我们举的例子并不是 DAG 导出的二分图，所以这个例子不能用来解释最长反链）：

令最大独立集为 $I$，考虑选出所有 $x_{out}$ 和 $x_{in}$ 都属于 $I$ 的点，记做集合 $A$，它们构成一个最长反链。

证明：
先证 $A$ 的确是一个反链：这是容易的，因为任取 $x \in A$，$x_{in}$ 就一定是被 DFS 到的点，而 $x_{out}$ 一定是没被 DFS 到的点，任何两个 $x, y \in A$ 之间若是有连边就和 DFS 的过程冲突了。
首先有 $|I| = 2n - |S| = 2n - m$，而 $|I| - |A|$ 可以看作是满足「$x_{out}$ 或 $x_{in}$ 属于 $I$」的 $x$ 的个数，显然这样的 $x$ 不会超过 $n$ 个，所以 $|I| - |A| \le n$，所以 $|A| \ge |I| - n = n - m$。
但是 $A$ 再大，也不能大过 $n - m$，所以 $|A| = n - m$，也就是一个最长反链。

总结——只要选出 $x_{out}$ 没被 DFS 到，且 $x_{in}$ 被 DFS 到了的点，这些点就组成一个最长反链。

然后是第三问，这只要默认该点被选中，也就是删除这个点和与其有偏序关系的所有点后，再求一次最长反链，如果最长反链的大小只减小了 $1$，那么这个点就能在最长反链中，否则不能。

下面是代码，复杂度为 $\mathcal O (n^{3.5})$：

#include <cstdio>
#include <algorithm>
#include <bitset>

namespace Dinic {
	const int Inf = 0x3f3f3f3f;
	const int MN = 205, MM = 5155;
	
	int N, S, T;
	int h[MN], iter[MN], nxt[MM * 2], to[MM * 2], w[MM * 2], tot;
	
	inline void Init(int _N) {
		N = _N, tot = 1;
		for (int i = 1; i <= N; ++i) h[i] = 0;
	}
	inline void SetST(int _S, int _T) { S = _S, T = _T; }
	
	inline void ins(int u, int v, int x) { nxt[++tot] = h[u], to[tot] = v, w[tot] = x, h[u] = tot; }
	inline void insw(int u, int v, int w1 = Inf, int w2 = 0) {
		if (!u) u = S; if (!v) v = T;
		ins(u, v, w1), ins(v, u, w2);
	}
	
	int lv[MN], que[MN], l, r;
	
	inline bool Lvl() {
		for (int i = 1; i <= N; ++i) lv[i] = 0;
		lv[S] = 1;
		que[l = r = 1] = S;
		while (l <= r) {
			int u = que[l++];
			for (int i = h[u]; i; i = nxt[i])
				if (w[i] && !lv[to[i]]) {
					lv[to[i]] = lv[u] + 1;
					que[++r] = to[i];
				}
		}
		return lv[T] != 0;
	}
	
	int Flow(int u, int f) {
		if (u == T) return f;
		int d = 0, s = 0;
		for (int &i = iter[u]; i; i = nxt[i])
			if (w[i] && lv[to[i]] == lv[u] + 1) {
				d = Flow(to[i], std::min(f, w[i]));
				f -= d, s += d;
				w[i] -= d, w[i ^ 1] += d;
				if (!f) break;
			}
		return s;
	}
	
	inline int DoDinic() {
		int Ans = 0;
		while (Lvl()) {
			for (int i = 1; i <= N; ++i) iter[i] = h[i];
			Ans += Flow(S, Inf);
		}
		return Ans;
	}
}
using Dinic::Init;
using Dinic::SetST;
using Dinic::insw;
using Dinic::DoDinic;
using Dinic::h;
using Dinic::nxt;
using Dinic::to;
using Dinic::w;

const int MN = 105;

int N, M, Ans;
std::bitset<101> g[MN];

int match[MN], tagl[MN], tagr[MN];
void DFS(int u) {
	tagr[u] = 1;
	for (int i = 1; i <= N; ++i)
		if (g[i][u] && !tagl[i])
			tagl[i] = 1, DFS(match[i]);
}

int main() {
	scanf("%d%d", &N, &M);
	for (int i = 1; i <= M; ++i) {
		int x, y;
		scanf("%d%d", &x, &y);
		g[x][y] = 1;
	}
	for (int k = 1; k <= N; ++k)
		for (int i = 1; i <= N; ++i)
			if (g[i][k]) g[i] |= g[k];
	Init(N + N + 2), SetST(N + N + 1, N + N + 2);
	for (int i = 1; i <= N; ++i)
		insw(0, i, 1), insw(N + i, 0, 1);
	for (int i = 1; i <= N; ++i)
		for (int j = 1; j <= N; ++j)
			if (g[i][j]) insw(i, N + j, 1);
	Ans = N - DoDinic();
	printf("%d\n", Ans);
	for (int i = 1; i <= N; ++i) if (!w[4 * i - 2]) {
		for (int j = h[i]; j; j = nxt[j])
			if (!w[j]) { match[i] = to[j] - N; break; }
	}
	for (int i = 1; i <= N; ++i) if (w[4 * i]) DFS(i);
	for (int i = 1; i <= N; ++i) printf("%d", !tagl[i] && tagr[i]);
	puts("");
	for (int u = 1; u <= N; ++u) {
		static int del[MN]; int cnt = 0;
		for (int i = 1; i <= N; ++i) del[i] = i == u || g[i][u] || g[u][i];
		Init(N + N + 2), SetST(N + N + 1, N + N + 2);
		for (int i = 1; i <= N; ++i) if (!del[i])
			insw(0, i, 1), insw(N + i, 0, 1), ++cnt;
		for (int i = 1; i <= N; ++i) if (!del[i])
			for (int j = 1; j <= N; ++j) if (!del[j])
				if (g[i][j]) insw(i, N + j, 1);
		printf("%d", cnt - DoDinic() == Ans - 1);
	} puts("");
	return 0;
}