自动搬运

查看原文

来自洛谷，原作者为

	DengDuck 澳門現役 OIer，萌萌未花日奈雙推人一枚

搬运于2025-08-24 21:58:21，当前版本为作者最后更新于2023-08-16 16:10:23，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

换根 DP 基础题。

这道题相当于问你，一棵树，选一个节点使得其到所有叶子节点的路径之和最小（因为路径上必然会经过所有节点）。

我们发现从一个点换到另外一个相邻的点中间相差的部分是很容易算出来的。

让我们画个图理解一手。

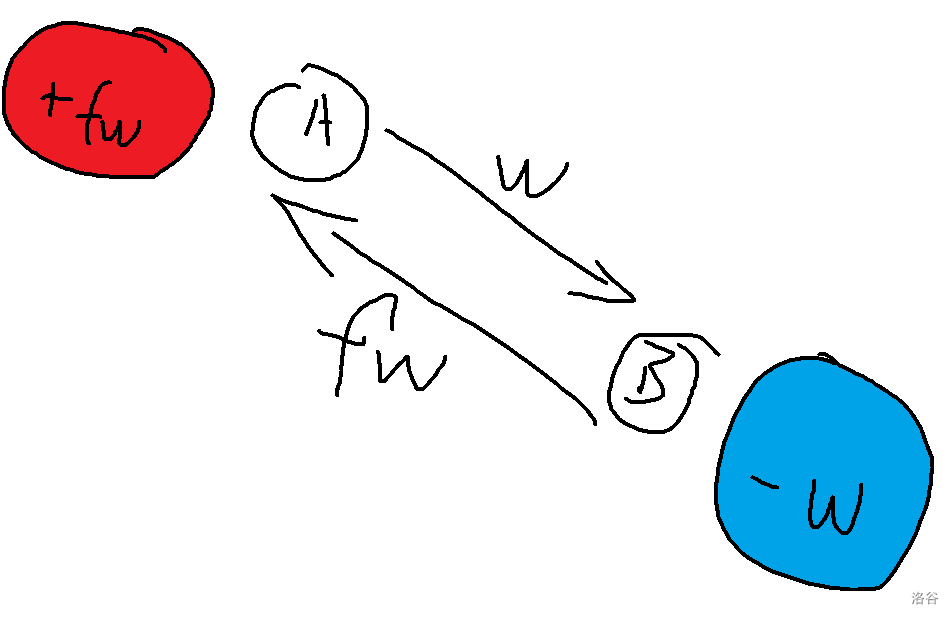
如图，我们进行转移 $A \to B$，边 $(A,B)=w,(B,A)=fw$，那么显然，蓝色部分的点到达我们选择的点距离减少了 $w$，而红色部分的点到我们选择的点距离增加了 $fw$。

我们需要预处理 $sz_x$ 表示 $x$ 子树中的叶子节点数量，根据这个数据，我们就知道每次转移需要减多少 $w$，加多少 $fw$，从而得到方程：

显然时间复杂度为 $\mathcal O(n)$ 的。

#include<bits/stdc++.h>
#define LL long long
using namespace std;
const LL N=1e5+5;
struct node
{
	LL to,w,fw;
};
LL n,tot[N],y,cnt,f[N],sz[N],ans=1e18;
vector<node>v[N];
vector<LL>a[N];
char c[N][25];
void get(LL x,LL fa,LL len)
{
	
	for(auto i:v[x])
	{
		if(i.to==fa)continue;
		get(i.to,x,len+i.w);
		sz[x]+=sz[i.to];
	}
	if(tot[x]==0)
	{
		f[1]+=len;
		cnt++;
		sz[x]++;		
	}

}
void dfs(LL x,LL fa)
{
	ans=min(ans,f[x]);
	for(auto i:v[x])
	{
		if(i.to==fa)continue;
		f[i.to]=f[x]-sz[i.to]*i.w+(cnt-sz[i.to])*i.fw;
		dfs(i.to,x);
	}
}
int main()
{
	scanf("%lld",&n);
	for(int i=1;i<=n;i++)
	{
		scanf("%s",c[i]);
		scanf("%lld",&tot[i]);
		for(int j=1;j<=tot[i];j++)
		{
			scanf("%lld",&y);
			a[i].push_back(y);
		}
	}
	for(int i=1;i<=n;i++)
	{	
		for(LL y:a[i])
		{
			LL t=strlen(c[y])+1;
			if(tot[y]==0)t--;
			v[i].push_back({y,t,3});
			v[y].push_back({i,3,t});
		}
	}
	get(1,0,0);
	dfs(1,0);
	printf("%lld\n",ans);
}