自动搬运

查看原文

来自洛谷，原作者为

	LawrenceSivan 人必须先说很多话，然后保持静默 || AFO

搬运于2025-08-24 21:58:03，当前版本为作者最后更新于2021-07-18 22:19:53，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

P4244 [SHOI2008]仙人掌图 II

前言

这是仙人掌的入门题目了。

这道题也让我学到了很多东西，所以来写一篇题解。

希望也能帮到大家qwq

题意

给定一个仙人掌，求出它的直径。

思路

看到求直径，首先可以联想到求树的直径。

对于树的直径，我们主要有两种方式：两次 DFS 或者 BFS，和树形 DP。

然后这个题直接使用 BFS 求解可以获得 70 分

具体做法是：

对于两次 BFS 或者 DFS ，首先任意地选择一个点，开始对树进行遍历，寻找最远的一个点，之后再从这个点开始，再次进行一次遍历，再次找到距离这个点最远的点。于是就求出了直径。关于证明可以从网上搜一搜，这里就不提了，今天的重点不是它

对于 DP ，可以得到以下过程：

void DP(int u){
	vis[u]=1;
	for(re int i=head[u];i;i=nxt[i]){
		int v=to[i];
		if(vis[v])continue;
		DP(v);
		ans=max(ans,f[u]+f[v]+val[i]);
		f[u]=max(f[u],f[v]+val[i]);
	}
}

但是对于仙人掌上的环，我们就不能这么去操作了。

考虑如何把仙人掌上的环消去。

需要使用圆方树。

如果你还不会圆方树

关于圆方树的概念及构造方法就不再多说了，这里主要是想说一说这道题的细节。

由于在构建圆方树的过程中，会把环变成一个菊花图，二这些针对的都是圆方树上方圆边或者圆方边。

对于树上的圆圆边是不会有影响的，因为环肯定不会出在圆圆边上。

所以对于圆方树的圆圆边，其实就是普通的树边，所以我们可以直接使用树形 DP 来进行转移。

如何判断到底是不是圆圆边呢？

根据定义，发现圆圆边不在环上，所以我们只需要判断两个点是不是满足不在环上就可以了。

回忆建树的 tarjan 过程，我们根据 dfs 序的大小以及 追溯值 low 来判断访问节点顺序的先后以及他们的位置关系。

当 low[v]>dfn[u] 时，说明 v 这个节点只能回到比 u 更靠下的位置上，所以他们不会组成一个环。

于是找出了圆圆边。

直接转移即可。

if(low[v]>dfn[u]){//不在环上，大力树形DP
            ans=max(ans,f[u]+f[v]+1);
            f[u]=max(f[u],f[v]+1);
        }

对于在环上的点，我们需要单独处理。

于是我们直接把这一条链都取出来单独来看。

问题在于我们如何找到一条链，就算找到了如何把它提取出来呢？

回忆 tarjan 的过程，也就是 dfs 的过程，每次都会沿着树边向前走，且每个点只会经过一次。

对于一个环，必定会有一条边经过不到。

如图所示：

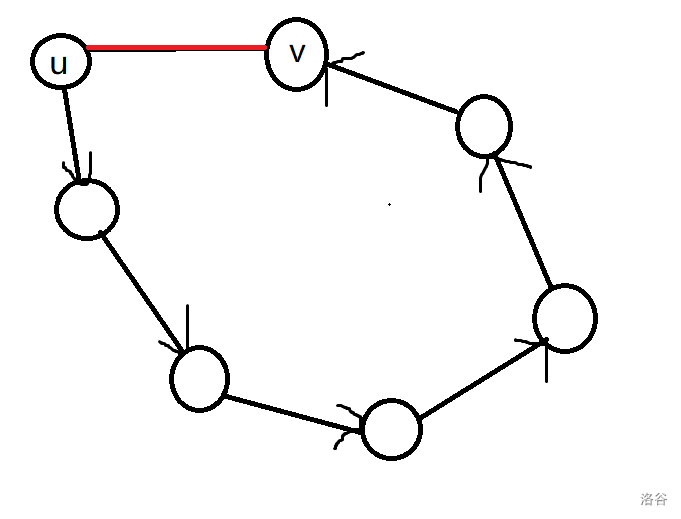
从 $u$ 出发，走到 $v$， 红色的边没有经过。

可以发现判断条件是 $v$ 在 $u$ 之后访问，并且 $v$ 在搜索树上的父亲不是 $u$ 。

于是一旦满足了这个条件，意味着我们当前找到的节点 $u$ 是一个环的起始，$v$ 是结束。

有了两头的节点，我们就可以顺势找出一整个环将它提取出来。

具体做法是从环的结束开始，每次跳他在搜索树中的父亲，直到调到环的起始为止。

可以用一个数组存储这个环。

有了环之后，我们需要计算环上的 dp 值了。

对于环上的两个点，如果想要计算 dp 数组的值，就需要知道两个节点在环上的距离。

注意在环上距离指的是两点较小的那个环上距离。

首先对于一个环，他的起始于结束部位相连的地方是不好处理的。

可以考虑环问题的套路处理方式：断环为链，复制一倍。

这样我们每次只计算不超过半个环长的部分，这样就可以找出较短的那一个了。

tot=0;
for(re int i=x;i!=fa[y];i=fa[i])g[++tot]=f[i];
for(re int i=1;i<=tot;i++)g[i+tot]=g[i];

转移方程是

ans=max(ans,f[i]+f[j]+(i-j))

其中，$i,j$ 分别是两个点，$f[i],f[j]$ 分别是对应点的 dp 值。

具体含义就是两个点的 dp 值之和加上两点在环上的距离。

发现这个式子只有一次项，是可以使用单调队列的。

发现这个式子其实就是求 $\max(f[i]+f[j]+(i-j))$ 。

循环的时候 $i$ 是定值，也就是要求 $\max(f[j]-j)$

所以得到维护队列单调性的条件：

g[q[tail]]-q[tail]<g[i]-i

上面的 $g[]$ 是 是为了方便转移的临时变量。

最后不要忘记更新环的起始位置的 dp 值。

细节相关

1. 对于每次提取链。

由于我们是沿着环按照 dfs 序递增的顺序访问的。

所以如果我们直接跳回环的起始位置，相当于我们的环是倒着存储的。

需不需要正过来呢？

不需要。

因为这个环本身就是任意的，你也不知道你会从哪里进来。

直接在环上 dp 就行了。

但是有一点需要注意。

如果你真的非要把他正过来，有一些细节需要注意。

观察这个图：

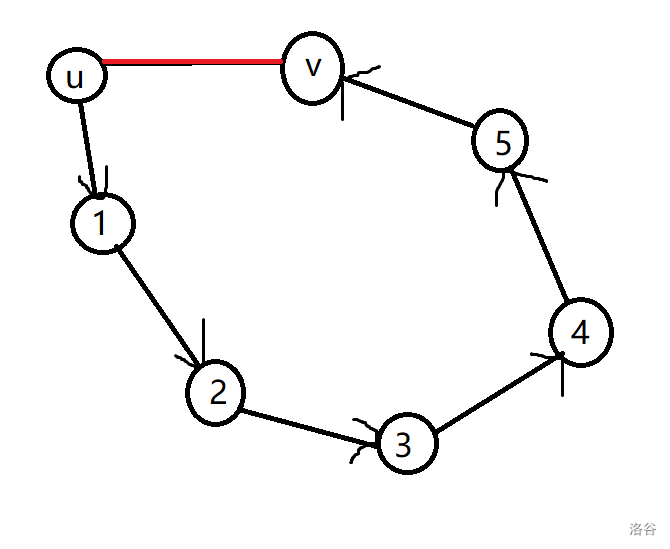
如果你直接跳回来，那么存环的序列就是：

$v\rightarrow 5\rightarrow 4 \rightarrow 3 \rightarrow 2 \rightarrow 1 \rightarrow u$

一号下标是 $v$。

而如果你反过来：

$u\rightarrow 1\rightarrow 2\rightarrow 3 \rightarrow4 \rightarrow 5 \rightarrow v$

一号下标是 $u$。

虽然 $u$ 也是环上的点，但是这个点一定是连接着一个圆圆边，而我们需要处理的第一个环上的边应该是 $u\rightarrow 1$ 这条边。

所以正过来的话需要从 $2$ 开始 dp，并且开始的决策集合需要补充上一个 $1$ 号点的决策点，才能保障正确进行。

关于最后根节点的 dp值更新：

同样的也要分开看，反着的直接更新：

for(re int i=1;i<=tot;i++)f[x]=max(f[x],g[i]+min(i,tot-i));

正着的需要注意， $1$ 号节点是不能更新的，需要从二号节点开始。

for(re int i=2;i<=tot;i++)f[x]=max(f[x],g[i]+min(i-1,tot-i+1));

同时给出正向和反向的代码：

正向：

//#define LawrenceSivan

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;
typedef unsigned long long ull;
#define INF 0x3f3f3f3f
#define re register
const int maxn=1e5+5;

int n,m,ans;

int hd[maxn],to[maxn<<1],nxt[maxn<<1],cnt;

inline void add(int u,int v){
    nxt[++cnt]=hd[u];
    to[cnt]=v;
    hd[u]=cnt;
}

int f[maxn],q[maxn],head,tail,g[maxn],tot;

//ans=max(ans,f[i]+f[j]+dis(i,j))
//dis(i,j)为他们在环上的较短距离
//为了保证是较短距离，断环为链，加倍处理，当长度超过半环就队头出队

int dfn[maxn],low[maxn],fa[maxn],num;

void solve(int x,int y){
    tot=0;
    for(re int i=y;i!=fa[x];i=fa[i])g[++tot]=f[i];
    for(re int i=1;i<=tot;i++)g[i+tot]=g[i];
    reverse(g+1,g+1+tot*2);
    head=1,tail=0;q[++tail]=1;
    for(re int i=2;i<=(tot<<1);i++){
        while(head<=tail&&i-q[head]>(tot>>1))head++;
        ans=max(ans,g[i]+g[q[head]]+(i-q[head]));
        while(head<=tail&&g[q[tail]]-q[tail]<g[i]-i)tail--;
        q[++tail]=i;
    }
    for(re int i=2;i<=tot;i++)f[x]=max(f[x],g[i]+min(i-1,tot-i+1));
}

void tarjan(int u){
    dfn[u]=low[u]=++num;
    for(re int i=hd[u];i;i=nxt[i]){
        int v=to[i];
        if(v==fa[u])continue;
        if(!dfn[v]){
            fa[v]=u;
            tarjan(v);
            low[u]=min(low[u],low[v]);
        }
        else low[u]=min(low[u],dfn[v]);
        if(low[v]>dfn[u]){//不在一个环上，大力树形DP
            ans=max(ans,f[u]+f[v]+1);
            f[u]=max(f[u],f[v]+1);
        }
    }
    for(re int i=hd[u];i;i=nxt[i]){
        int v=to[i];
        if(fa[v]==u)continue;//要找的是非树边，树边不要
        if(dfn[v]>dfn[u])solve(u,v);//找到环的两个端点，把环拎出来单独算
    }
}

template<typename T>
inline void read(T &x){
    x=0;T f=1;char ch=getchar();
    while (!isdigit(ch)) {if(ch=='-')f=-1;ch=getchar();}
    while (isdigit(ch)){x=x*10+(ch^48);ch=getchar();}
    x*=f;
}

signed main() {
#ifdef LawrenceSivan
    freopen("aa.in", "r", stdin);
    freopen("aa.out", "w", stdout);
#endif
    read(n),read(m);
    for(re int i=1,x,u,v;i<=m;i++){
        read(x);read(u);x--;
        while(x--){
            read(v);add(u,v);add(v,u);u=v;
        }
    }

    tarjan(1);

    printf("%d\n",ans);


    return 0;
}

反向

//#define LawrenceSivan

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;
typedef unsigned long long ull;
#define INF 0x3f3f3f3f
#define re register
const int maxn=1e5+5;

int n,m,ans;

int hd[maxn],to[maxn<<1],nxt[maxn<<1],cnt;

inline void add(int u,int v){
    nxt[++cnt]=hd[u];
    to[cnt]=v;
    hd[u]=cnt;
}

int f[maxn],q[maxn],head,tail,g[maxn],tot;

//ans=max(ans,f[i]+f[j]+dis(i,j))
//dis(i,j)为他们在环上的较短距离
//为了保证是较短距离，断环为链，加倍处理，当长度超过半环就队头出队

int dfn[maxn],low[maxn],fa[maxn],num;

void solve(int x,int y){
    tot=0;
    for(re int i=y;i!=fa[x];i=fa[i])g[++tot]=f[i];
    for(re int i=1;i<=tot;i++)g[i+tot]=g[i];
    head=1,tail=0;q[++tail]=0;
    for(re int i=1;i<=(tot<<1);i++){
        while(head<tail&&i-q[head]>(tot>>1))head++;
        ans=max(ans,g[i]+g[q[head]]+(i-q[head]));
        while(head<tail&&g[q[tail]]-q[tail]<g[i]-i)tail--;
        q[++tail]=i;
    }
    for(re int i=1;i<=tot;i++)f[x]=max(f[x],g[i]+min(i,tot-i));
}

void tarjan(int u){
    dfn[u]=low[u]=++num;
    for(re int i=hd[u];i;i=nxt[i]){
        int v=to[i];
        if(v==fa[u])continue;
        if(!dfn[v]){
            fa[v]=u;
            tarjan(v);
            low[u]=min(low[u],low[v]);
        }
        else low[u]=min(low[u],dfn[v]);
        if(low[v]>dfn[u]){//不在一个环上，大力树形DP
            ans=max(ans,f[u]+f[v]+1);
            f[u]=max(f[u],f[v]+1);
        }
    }
    for(re int i=hd[u];i;i=nxt[i]){
        int v=to[i];
        if(fa[v]==u)continue;//要找的是非树边，树边不要
        if(dfn[v]>dfn[u])solve(u,v);//找到环的两个端点，把环拎出来单独算
    }
}

template<typename T>
inline void read(T &x){
    x=0;T f=1;char ch=getchar();
    while (!isdigit(ch)) {if(ch=='-')f=-1;ch=getchar();}
    while (isdigit(ch)){x=x*10+(ch^48);ch=getchar();}
    x*=f;
}

signed main() {
#ifdef LawrenceSivan
    freopen("aa.in", "r", stdin);
    freopen("aa.out", "w", stdout);
#endif
    read(n),read(m);
    for(re int i=1,x,u,v;i<=m;i++){
        read(x);read(u);x--;
        while(x--){
            read(v);add(u,v);add(v,u);u=v;
        }
    }

    tarjan(1);

    printf("%d\n",ans);


    return 0;
}