自动搬运

查看原文

来自洛谷，原作者为

	hs_black Go for broke

搬运于2025-08-24 21:57:46，当前版本为作者最后更新于2020-01-23 21:32:42，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

推销一波个人博客

来一发无脑的主席树解法⑧

前置芝士: 主席树

主席树亦称可持久化线段树, 它可以轻松的解决二维偏序问题, 如区间第k大, 区间不同颜色个数等问题, 不会的同学可以模板区自行学习一下

回到本题:

利用主席树, 我们可以快速的求出区间[L, R]完全覆盖的"熊孩子区间"个数, 具体来说, 对于每个"熊孩子区间"[l, r], 以左端点l 为下标, 右端点r为权值, 建立主席树. 查询区间[L, R]时, 只需拿R处的线段树减去L-1处的线段树求出[L, R]的区间和即可

定义合并两个区间$[l_1, r_1], [l_2, r_2]$新产出的答案个数为:

区间$[l_1, r_2]$包含的熊孩子区间减去$[l_1, r_1]$的区间个数再减去 $[l_2, r_2]$包含的区间个数

那么本题中每次消掉一个气球, 如果消掉气球以后此处气球个数不为零, 显然对答案没有影响, 否则将起到合并相邻的两个区间的作用

如下图, 轴上是位置, 下面是气球个数

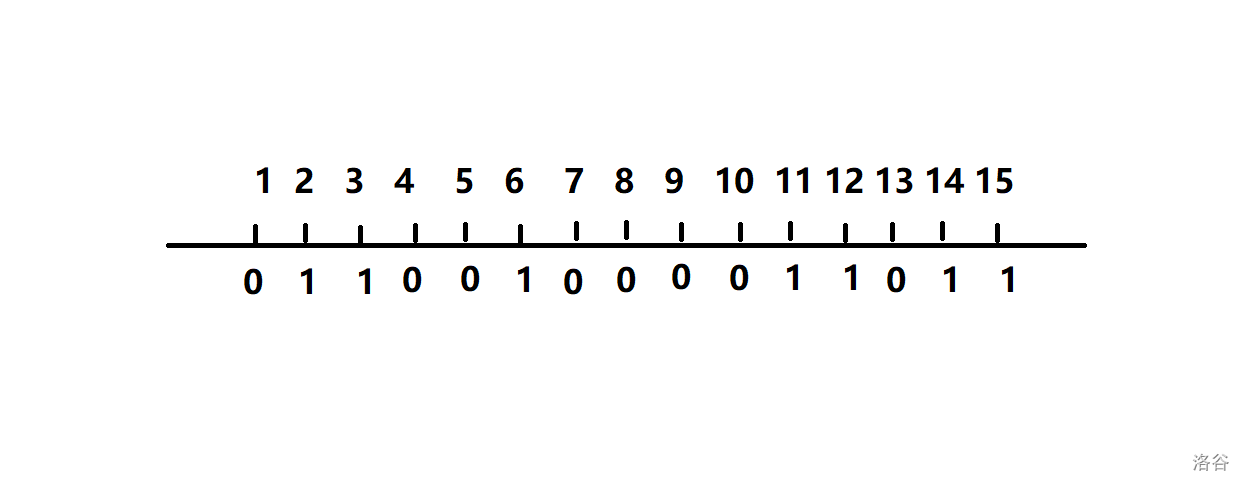
假如本次将6处的气球????点爆, 多出的答案可以这样算, 先将区间[4, 5] 和 [6, 6]合并, 在将[4, 6]和[7, 10]合并, 注意要用并查集维护

#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <vector>

using namespace std;
const int N = 500500;

template <typename T>
void read(T &x) {
    x = 0; bool f = 0;
    char c = getchar();
    for (;!isdigit(c);c=getchar()) if (c=='-') f=1;
    for (;isdigit(c);c=getchar()) x=x*10+(c^48);
    if (f) x=-x;
}

int box[N], cnt, n, m;
vector<int> v[N];

int lastans = 0;

int ls[N*4], rs[N*4], T[N*4], sum[N*4];
int update(int pre, int l, int r, int x) {
    int rt = ++cnt;
    sum[rt] = sum[pre] + 1;
    ls[rt] = ls[pre], rs[rt] = rs[pre];
    int mid = (l + r) >> 1;
    if (l < r) {
        if (x <= mid) ls[rt] = update(ls[pre], l, mid, x);
        else rs[rt] = update(rs[pre], mid + 1, r, x);
    }
    return rt;
}

int ql, qr;
int query(int pre, int now, int l, int r) {
    if (l >= ql && r <= qr) return sum[now] - sum[pre];
    int mid = (l + r) >> 1;
    int res = 0;
    if (ql <= mid) res += query(ls[pre], ls[now], l, mid);
    if (qr > mid) res += query(rs[pre], rs[now], mid + 1, r);
    return res;
}

void merge(int l1, int r1, int l2, int r2) {
    ql = l1, qr = r1;
    lastans -= query(T[l1-1], T[r1], 1, n);
    ql = l2, qr = r2;
    lastans -= query(T[l2-1], T[r2], 1, n);
    ql = l1, qr = r2;
    lastans += query(T[l1-1], T[r2], 1, n);
}

int f[N], L[N], R[N];

int find(int x) {
    return f[x] == x ? x : f[x] = find(f[x]);
}
int main() {
    read(n), read(m);
    for (int i = 1;i <= n; i++) read(box[i]), L[i] = R[i] = f[i] = i;
    for (int i = 1;i <= m; i++) {
        int l, r; read(l), read(r);
        v[l].push_back(r);
    } cnt = T[0] = 1;
    for (int i = 1;i <= n; i++) {
        T[i] = T[i-1];
        for (int j = 0;j < v[i].size(); j++)
            T[i] = update(T[i], 1, n, v[i][j]);
    }
    int k; read(k);
    for (int i = 1;i <= k; i++) {
        int a; read(a); a = (a + lastans - 1) % n + 1;
        box[a]--;
        if (!box[a]) {
        	ql = a, qr = a;
        	lastans += query(T[a-1], T[a], 1, n);
            if (a != 1 && !box[a-1]) {
                int fx = find(a-1); f[a] = fx; 
                merge(L[fx], R[fx], a, a); R[fx] = a;
            }
            if (a != n && !box[a+1]) {
                int fx = find(a+1), fy = find(a);
                merge(L[fy], R[fy], L[fx], R[fx]);
                f[fy] = fx, L[fx] = L[fy];
            }
        }
        printf ("%d\n", lastans);
    }
    return 0;
}