自动搬运

查看原文

来自洛谷，原作者为

	SuperJvRuo **

搬运于2025-08-24 21:57:40，当前版本为作者最后更新于2018-03-04 16:34:24，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

蒟蒻写了一上午才把这题写明白T_T，这篇题解是给刚接触计算几何、simpson公式的同学们看的，有基础请看其他dalao题解。

题意

求一棵由圆台、圆锥组成的树在平行光下的投影。

分析

圆台投在地上形成圆和梯形；圆锥投在地上形成圆和三角形。圆投在地上，得到一个与原来等大的圆，梯形和三角形的高变为原来的$\frac{1}{tan(\alpha)}$，像这样(图片由Windows10自带的画图3D制作)：

如果树更复杂一点，可能是这样（下图来自CSDN）

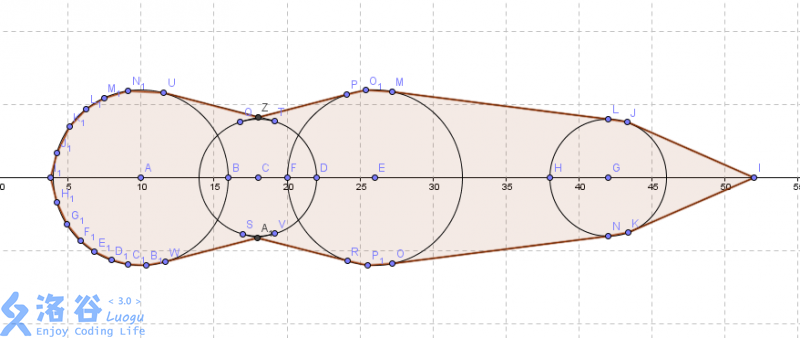
我们要求的就是这样的面积并。

咋求啊？

Section 1：Simple Simpson公式

自适应Simpson公式(adaptive Simpson's rule)是一种像二分法、三分法一样的数值方法。我们先来看Simpson公式：

$$\int ^b_a f(x)dx=(b-a)\frac{f(a)+4f(\frac{a+b}{2})+f(b)}{6} $$

就这么搞？这公式准确吗？

当然……不准确了。但是把整个函数分成若干段，分开计算Simpson，分段越多，越接近准确值，但计算量也就越大。我们可以这样搞：取$[a,b]$的中点$c$，当$|S(a,c)+S(c,b)-S(a,b)|<EPS$时返回结果，否则递归下去，像这样：

#define EPS 1e-7

double F(double x)
{
	//do something
}

//三点Simpson法，这里要求F是一个全局函数
double simpson(double a, double b)
{
	double c = a + (b - a) / 2.0;
    return (b - a) * (F(a) + 4.0 * F(c) + F(b)) / 6.0;
}

//自适应Simpson公式
double asr(double a, double b, double ans)
{
	double c = a + (b - a) / 2.0;
    double left = simpson(a, c), right = simpson(c, b);
    if(fabs(left + right - ans) < EPS)
    	return left + right;
    else
    	return asr(a, c, left) + asr(c, b, right);
}

int main()
{
	printf("%lf", asr(simpson(l, r, simpson(l, r))));
    return 0;
}

这就很SimpleSimpson了是不是？

Section 2：计算几何——求公切线

我们发现，圆形和梯形是这样合并的：

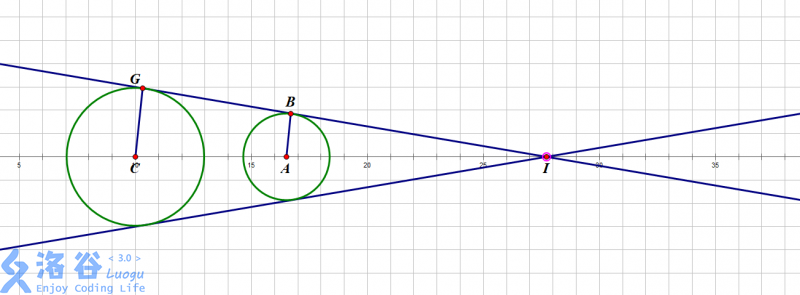
梯形的两腰正是两个圆的公切线。本题需要公切线的左右两端的横坐标（即把这一段视为函数后的定义域），斜率，和纵截距。

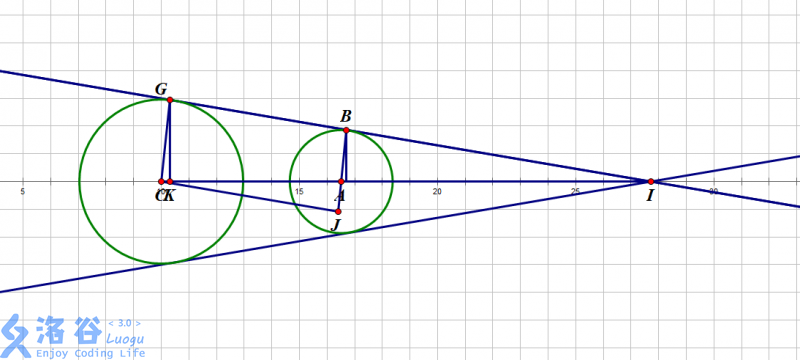
如图，$x$轴是影子的对称轴，$\bigodot A$与$\bigodot C$的公切线之一是直线$BG$，过点$G$、点$B$分别作$x$轴的垂线。四边形$BJCG$是矩形。原点$O$是柠檬树的树根（在屏幕外面）。

由圆台高度和$\alpha$的余切值，我们可以求出线段$OC,OA$的长度，即可得$AC=OA-OC$。

由两个圆的半径可得$AJ=CG-AB$。

显然，$sin\angle CGK=sin\angle ACJ=\frac{AJ}{AC}$，$CK=sin\angle CGK \cdot CG$，$OK=OC+CK$，$OK$的值即为定义域的左端。我们也可以以相同方法求出$\bigodot A$切点的横坐标，即定义域右端。

然后我们就可以通过勾股定理求出$GK$的长，进而得到$G$的坐标，对$B$进行相同处理后，确定了公切线上的两点，我们就可以得到公切线的斜率与纵截距，求出公切线的解析式。

至此，这道题的所有难点都已经攻破，上代码！

#include<cstdio>
#include<cmath>
#define EPS 1e-7

double alpha;
int n;
struct circle
{
	double x, r;
	//x为投影圆心到树根的距离，r为半径 
}p[1000];

struct tan_line
{
	double k, b, left, right;
	//f(x)=kx+b,x∈[left,right]
}q[1000];

double Gougu(double a, double b)//a是斜边 
{
	return sqrt(a*a - b * b);
}

void get_tan(int x, int y)
{
	if (fabs(p[x].r - p[y].r)<EPS)//实数比较记得带上EPS 
	{
		q[x].left = p[x].x;
		q[x].right = p[y].x;
		q[x].k = 0; q[x].b = p[x].r;
		return;
	}
	double dx = p[y].x - p[x].x, dr = fabs(p[x].r - p[y].r);
	//dx即图中的AC，dr即图中的AJ 
	double ly, ry;
	if (p[x].r>p[y].r)
	{
		q[x].left = p[x].x + p[x].r*dr / dx;//公切线左端 
		q[x].right = p[y].x + (q[x].left - p[x].x)*p[y].r / p[x].r;//公切线右端 
		ly = Gougu(p[x].r, q[x].left - p[x].x);//勾股定理求F(left)
		ry = Gougu(p[y].r, q[x].right - p[y].x);//勾股定理求F(right) 
		q[x].k = (ly - ry) / (q[x].left - q[x].right);//求斜率 
		q[x].b = ly - q[x].left*q[x].k;//求纵截距 
	}
	else//另一种情况，同理 
	{
		q[x].right = p[y].x - p[y].r*dr / dx;
		q[x].left = p[x].x - (p[y].x - q[x].right)*p[x].r / p[y].r;
		ly = Gougu(p[x].r, q[x].left - p[x].x);
		ry = Gougu(p[y].r, q[x].right - p[y].x);
		q[x].k = (ly - ry) / (q[x].left - q[x].right);
		q[x].b = ly - q[x].left*q[x].k;
	}
}

double F(double x)
{
	double ans = 0.0;
	for (int i = 1; i <= n; ++i)
	{
		if (x<p[i].x + p[i].r&&x>p[i].x - p[i].r)//x在这一段内 
		{
			//迭代答案 
			ans = ans>Gougu(p[i].r, x - p[i].x) ? ans : Gougu(p[i].r, x - p[i].x);
		}
	}
	for (int i = 1; i <= n; ++i)
	{
		if (x >= q[i].left&&x <= q[i].right)//x在这一段内 
		{
			//迭代答案 
			ans = ans>q[i].k*x + q[i].b ? ans : q[i].k*x + q[i].b;
		}
	}
	return ans;
}

//三点Simpson法 
double simpson(double a, double b)
{
	double c = a + (b - a) / 2.0;
	return (b - a) * (F(a) + 4.0 * F(c) + F(b)) / 6.0;
}

//自适应Simpson公式 
double asr(double a, double b, double ans)
{
	double c = a + (b - a) / 2.0;
	double left = simpson(a, c), right = simpson(c, b);
	if (fabs(left + right - ans) < EPS)
	{
		return left + right;
	}
	else
	{
		return asr(a, c, left) + asr(c, b, right);
	}
}

int main()
{
	scanf("%d %lf", &n, &alpha);
	alpha = 1.0 / tan(alpha);//我们只会用到cot(alpha) 
	scanf("%lf", &p[1].x);
	p[1].x *= alpha;
	for (int i = 2; i <= n + 1; ++i)
	{
		scanf("%lf", &p[i].x);
		p[i].x *= alpha;
		p[i].x += p[i - 1].x;
	}
	for (int i = 1; i <= n; ++i)
		scanf("%lf", &p[i].r);
	++n;
	p[n].r = 0.0;//树顶是圆锥 
	for (int i = 1; i <= n - 1; ++i)
	{
		get_tan(i, i + 1);//求i与i+1间的切线 
	}

	//迭代整个影子的最低点和最高点 
	double ll = p[1].x - p[1].r, rr = p[n].x;
	for (int i = 1; i <= n; ++i)
	{
		rr = rr>(p[i].x + p[i].r) ? rr : (p[i].x + p[i].r);
		ll = ll<(p[i].x - p[i].r) ? ll : (p[i].x - p[i].r);
	}
	printf("%.2lf\n", 2.0*asr(ll, rr, simpson(ll, rr)));
	//我们只算了影子的一半，所以还要乘2 
	return 0;
}