自动搬运

查看原文

来自洛谷，原作者为

	bztMinamoto **

搬运于2025-08-24 21:57:34，当前版本为作者最后更新于2018-09-20 14:53:44，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

更好的阅读体验->这里

据说离线做法是主席树上树+启发式合并（然而我并不会）

据说bzoj上有强制在线版本只能用克鲁斯卡尔重构树，那就好好讲一下好了

这里先感谢LadyLex大佬的博客->这里

克鲁斯卡尔重构树可以用来解决一类诸如“查询从某个点出发经过边权不超过val的边所能到达的节点”的问题

首先不难发现，上面这个问题肯定是在最小生成树上走最优，其他边都可以不用去管

那么我们就在建最小生成树的时候搞事情

克鲁斯卡尔重构树的思想就是在建最小生成树的时候不是直接连边，而是新建一个节点，并把这个节点的值设为边权，然后令两个连通块的代表点分别作为它的左右儿子。然后令这个新节点成为整个连通块的代表点

说了那么多跟没说一样……举个栗子好了

假设现在有四个节点，要求他们的克鲁斯卡尔重构树

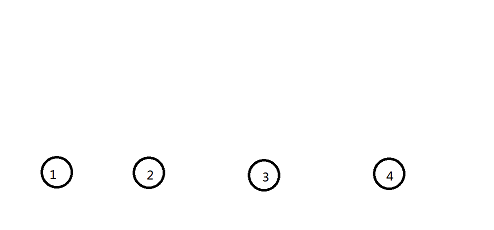
我们按最小生成树的方法找，先把边按权值从小到大排序。

然后设第一条边权值为4，连接1和2这两个连通块

然后新建一个节点5，点权设为4，并把1和2作为他的左右儿子

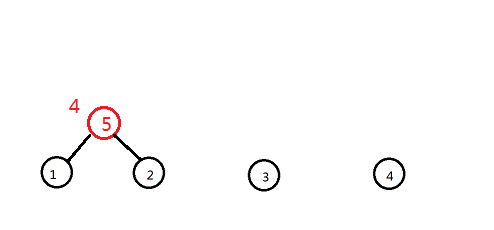
第二条边权值为6，连接3和4这两个连通块

然后新建一个节点6，点权设为6，并把3和4作为他的左右儿子

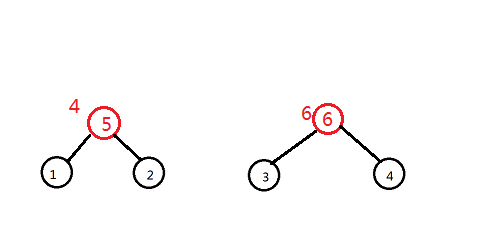
第三条边权值为7，连接1和2，那么我们就是要把4和6的连通块相连了（这两个是连通块的代表点）

然后新建一个节点7，点权设为7，并把5和6作为他的左右儿子

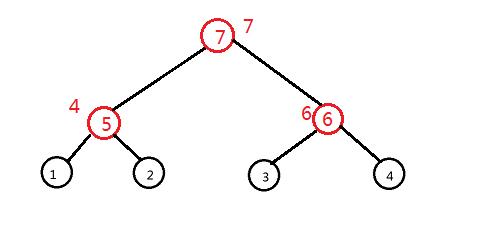
然后这一棵克鲁斯卡尔重构树就建好了٩(๑>◡<๑)۶

不难发现它有一个性质，每一个儿子节点的权值都小于等于自己的权值（因为我们是按最小生成树的顺序建的）

那么要查“查询从某个点出发经过边权不超过val的边所能到达的节点”

因为我们一个原来图上的点肯定是叶子结点，所以我们只要从叶子结点开始往上找，直到找到最后一个点权小于等于$val$的点

那么这个点为根的子树里的所有点都能到达

怎么找呢？倍增就行了

放到这一题里，因为要查询第$k$大，所以还得套个主席树上树

然而就差不多了

//minamoto
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define getc() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
char buf[1<<21],*p1=buf,*p2=buf;
inline int read(){
    #define num ch-'0'
    char ch;bool flag=0;int res;
    while(!isdigit(ch=getc()))
    (ch=='-')&&(flag=true);
    for(res=num;isdigit(ch=getc());res=res*10+num);
    (flag)&&(res=-res);
    #undef num
    return res;
}
char sr[1<<21],z[20];int C=-1,Z;
inline void Ot(){fwrite(sr,1,C+1,stdout),C=-1;}
inline void print(int x){
    if(C>1<<20)Ot();if(x<0)sr[++C]=45,x=-x;
    while(z[++Z]=x%10+48,x/=10);
    while(sr[++C]=z[Z],--Z);sr[++C]='\n';
}
const int N=2e5+5,M=N*16,K=5e5+5;
struct node{
	int from,to,cost;
	node(){}
	node(int from,int to,int cost):from(from),to(to),cost(cost){}
	inline bool operator <(const node &b)const
	{return cost<b.cost;}
}E[K];
int head[N],Next[N],ver[N],sum[M],L[M],R[M],bin[25],cnt,tot;
int fa[N],f[N][20],ls[N],rs[N],rt[N],val[N],num;
int h[N],limit,b[N],n,q,m,ans=0,dfn;
inline void mission(int u){
	for(int i=1;bin[i]<=n;++i)
	f[u][i]=f[f[u][i-1]][i-1];
}
inline void add(int u,int v){
	ver[++tot]=v,Next[tot]=head[u],head[u]=tot;
}
int find(int x){return x==fa[x]?x:fa[x]=find(fa[x]);}
void update(int last,int &now,int l,int r,int x){
	sum[now=++cnt]=sum[last]+1;
	if(l==r) return;
	int mid=(l+r)>>1;
	if(x<=mid) R[now]=R[last],update(L[last],L[now],l,mid,x);
	else L[now]=L[last],update(R[last],R[now],mid+1,r,x);
}
int query(int a,int x,int k){
	int l=1,r=limit;
	for(int j=18;~j;--j)
	if(f[a][j]&&val[f[a][j]]<=x) a=f[a][j];
	int v=rt[rs[a]],u=rt[ls[a]-1];
	if(sum[v]-sum[u]<k) return -1;
	while(l<r){
		int tmp=sum[R[v]]-sum[R[u]],mid=(l+r)>>1;
		if(tmp>=k) v=R[v],u=R[u],l=mid+1;
		else v=L[v],u=L[u],r=mid,k-=tmp;
	}
	return b[r];
}
void dfs(int u){
	mission(u),ls[u]=++num;
	if(u<=n) update(rt[num-1],rt[num],1,limit,h[u]);
	else rt[num]=rt[num-1];
	for(int i=head[u];i;i=Next[i]) dfs(ver[i]);
	rs[u]=num;
}
int main(){
//	freopen("testdata.in","r",stdin);
	n=read(),m=read(),q=read();
	bin[0]=1;for(int i=1;i<=22;++i) bin[i]=bin[i-1]<<1;
	for(int i=1;i<=2*n;++i) fa[i]=i;
	for(int i=1;i<=n;++i) b[i]=h[i]=read();
	for(int i=1,u,v,e;i<=m;++i)
	u=read(),v=read(),e=read(),E[i]=node(u,v,e);
	sort(b+1,b+1+n),limit=unique(b+1,b+1+n)-b-1;
	for(int i=1;i<=n;++i) h[i]=lower_bound(b+1,b+1+limit,h[i])-b;
	sort(E+1,E+1+m);dfn=n;
	for(int i=1;i<=m;++i){
		int u=find(E[i].from),v=find(E[i].to);
		if(u!=v){
			val[++dfn]=E[i].cost,fa[u]=fa[v]=dfn;
			add(dfn,u),add(dfn,v),f[u][0]=f[v][0]=dfn;
			if(dfn-n==n-1) break;
		}
	}
	for(int i=1;i<=dfn;++i) if(!ls[i]) dfs(find(i));
	while(q--){
		int v=read(),x=read(),k=read();
		print(query(v,x,k));
	}
	Ot();
	return 0;
}