自动搬运

查看原文

来自洛谷，原作者为

	Grisses 苹果没有色彩，它只是在反射760~622nm波长的光而已，带来色彩的不过是大脑皮层上的电信号罢了～

搬运于2025-08-24 21:57:34，当前版本为作者最后更新于2022-04-09 13:32:25，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

upd:

2023/7/28 图炸了，补一下

---

题面

建议放大 $150\%$ 食用 （否则看不清别怪我）

蒟蒻第一篇算为详细的题解，讲得不够清楚的还望多多包涵。

首先，看看题目名称，就能知道本题是一道半平面交的模板题。

一、定义

1、半平面

一条直线和直线的一侧。半平面是一个点集，因此是一条直线和直线的一侧构成的点集。当包含直线时，称为闭半平面；当不包含直线时，称为开半平面。

解析式一般为 $Ax+By+C\ge0$ 或 $Ax+By+C>0$。

如下图黄色部分就是解析式为 $Ax+By+C>0$ 的半平面。

2、半平面交

几个半平面的交集。因为半平面是点集，所以半平面交也是点集。

二、解法（S&I 算法）

1、前置

（一）直线

这里用向量来表示直线，半平面为向量的左侧部分。

（二）求交点

对于 $\vec{a}(start_{\vec{a}},end_{\vec{a}})$ 和 $\vec{b}(start_{\vec{b}},end_{\vec{b}})$ 两个向量表示的直线的交点 O，有：

$$x_O=(S_1\times x_{start_{\vec{b}}}-S_2\times x_{end_{\vec{b}}})/(S_1-S_2) $$$$y_O=(S_1\times y_{start_{\vec{b}}}-S_2\times y_{end_{\vec{b}}})/(S_1-S_2) $$

其中 $S_1,S_2$ 分别为 $(end_{\vec{b}}-start_{\vec{a}})\times(end_{\vec{a}}-start_{\vec{a}})$ 和 $(start_{\vec{b}}-start_{\vec{a}})\times(end_{\vec{a}}-start_{\vec{a}})$（向量叉积）。

证明：

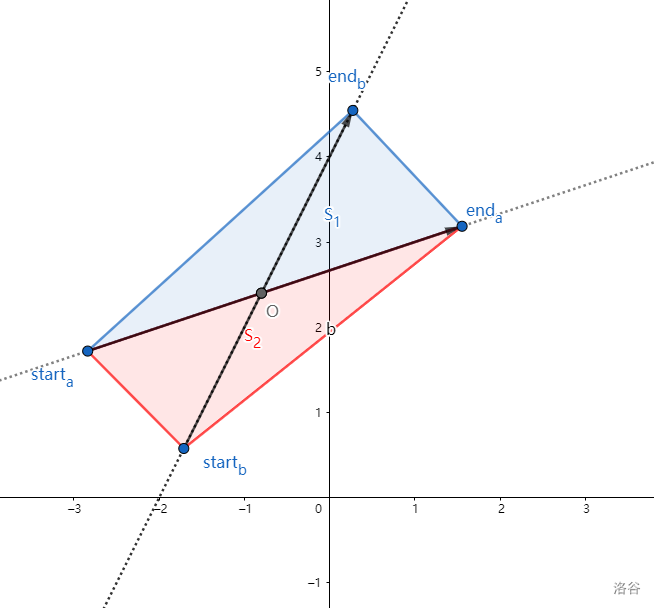
由共边定理可得：$\dfrac{end_{\vec{b}}\,O}{O\,start_{\vec{b}}}=\dfrac{S_1}{S_2}$（有向线段长和有向面积）。然后又因为 $S_1,S_2$ 是用向量叉积算的所以满足条件。得证。

（三）凸包

如果您不会凸包的话，这边建议出门左转二维凸包。

（四）极角

极角就是向量与 $x$ 轴的夹角（有向）。

对于一条起点和终点分别为 $A(x_A,y_A)$ 和 $B(x_b,y_b)$ 的向量所代表的直线，它的极角在 c++ 里表示为：

atan2(y[B]-y[A],x[B]-x[A])

其实就是斜率。

2、算法实现

首先，我们先按极角给所有向量排序，极角小的排在前面，如果极角相同。因为我们求的是向量左侧的半平面的交集，所以优先选择靠左的半平面，用向量叉积判断即可。排序后，以极角为标准去下重。

然后，我们维护一个双端队列。双端队列用来存储目前所有用来表示半平面交的边的向量。对于每个向量，我们先对其检查，如果双端队列里后两条向量的交点在这条向量的右侧。那么，弹出双端队列的最后一条向量，直到满足要求为止。接下来，对双端队列前面的向量重复上述操作。再把当前向量插入双端队列。

最后，对双端队列内部的向量进行检验，弹出不合法的向量。再求面积就行了。

三、代码

  #include<bits/stdc++.h>
  #define db double
  using namespace std;
  int n,cnt,tot,top,back;
  db ans;
  const db eps=1e-7;//因为是实数范围，有精度误差，所以不能直接用“==”，而是取绝对值和一个很小的值进行比对。
  struct node{
      db x,y;
      node(){}
      node(db _x,db _y){x=_x,y=_y;}
      bool operator<(const node &t)const{return y<t.y||(y==t.y&&x<t.x);}
      node operator-(node &t){return node(x-t.x,y-t.y);}
      bool operator==(const node &t)const{return x==t.x&&y==t.y;}
  }_P,N[55],Ans[505];//存储点
  db CPr(node A,node B){return A.x*B.y-A.y*B.x;}
  db CPr(node A,node B,node C){return CPr(B-A,C-A);}//向量叉积
  struct edge{
      node start,end;
      db angle;
      edge(){}
      edge(node A,node B){
          start=A,end=B;//起点和终点
          angle=atan2((B-A).y,(B-A).x);//极角
      }
      bool operator<(const edge &t)const{
          if(fabs(angle-t.angle)<=eps)return CPr(start,t.start,t.end)>0;//极角相同比位置
          return angle<t.angle;//否则比极角
      }
  }e[505],dq[505];//存储向量
  db S1,S2;
  node getnode(edge A,edge B){
      S1=CPr(A.start,B.end,A.end);
      S2=CPr(A.start,B.start,A.end);
      return node((S1*B.start.x-S2*B.end.x)/(S1-S2),(S1*B.start.y-S2*B.end.y)/(S1-S2));
  }
  bool ch(edge A,edge B,edge C){
      _P=getnode(B,C);
      return CPr(_P,A.start,A.end)<0;
  }//求交点
  signed main()
  {
      scanf("%d",&n);
      for(int i=1,m;i<=n;i++){
          scanf("%d",&m);
          for(int j=1;j<=m;j++)scanf("%lf%lf",&N[j].x,&N[j].y);
          for(int j=1;j<=m;j++)e[++cnt]=edge(N[j],N[j%m+1]);//读点，构建向量
      }
      sort(e+1,e+cnt+1);//排序
      tot=1;
      for(int i=2;i<=cnt;i++)if(fabs(e[i].angle-e[i-1].angle)>eps)e[++tot]=e[i];//去重
      top=2,back=1;
      dq[1]=e[1];
      dq[2]=e[2];
      for(int i=3;i<=tot;i++){
          while(back<top&&ch(e[i],dq[top],dq[top-1]))top--;
          while(back<top&&ch(e[i],dq[back],dq[back+1]))back++;
          dq[++top]=e[i];//增量
      }
      while(back<top&&ch(dq[back],dq[top-1],dq[top]))top--;
      while(back<top&&ch(dq[top],dq[back],dq[back+1]))back++;//弹出不合法的向量
      for(int i=back;i<top;i++)Ans[i-back+1]=getnode(dq[i],dq[i+1]);//求交点
      if(top-back>1)Ans[top-back+1]=getnode(dq[top],dq[back]);
      tot=top-back+1;
      for(int i=1;i<=tot;i++)ans+=CPr(Ans[i],Ans[i%tot+1]);//算面积
      printf("%.3lf",fabs(ans)/2);
      return 0;
  }