1 条题解
-
0
自动搬运
来自洛谷,原作者为

lcjqwq
赠你满天星搬运于
2025-08-24 21:57:14,当前版本为作者最后更新于2018-09-02 22:28:57,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
upd 2018.09.16 发现自己的图没了,重新审核
神仙分块题。。
Description
给出一个长度为 序列 , 次询问,每次询问区间 里的众数(出现次数最多的数)。若有多个,输出最小的。
,强制在线。
Solution
,先离散化。然后
算法一:暴力 ,预计得分 20 ; 实际得分 20 (开了 O2 直接变成 85 啥操作)
算法二: , 看来需要搬出分块大法。
预处理出两个数组:
:表示第 个块 到第 个块的(最小的)众数。
:类似于前缀和,在前 个(包括 )个块中 (离散化之后的值)出现了几次。
如何预处理
对于 ,直接每个块扫一遍,复杂度
对于 ,双重循环枚举 ,开一个数组暴力统计每个数出现了多少次。复杂度
预处理 有啥用呢?对于一个询问 ,设 在第 个块中, 在第 个块中。那么分两种情况:
第一种:,直接暴力扫 ,复杂度
第二种:,如下图:
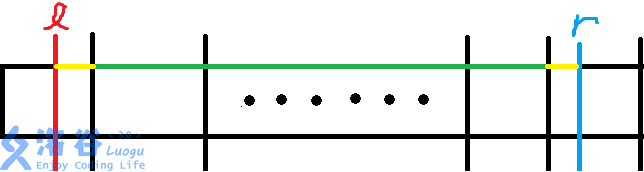
红线就是 ,蓝线就是 ,黑线是块与块的分割线。
答案
绿线的众数在之前已经预处理好了,对于黄线中的每一个元素在区间中出现的次数就是 在黄线中出现的次数 + 在绿线中出现的次数。
对于在黄线中出现的次数,可以直接扫,复杂度
对于在绿线中出现的次数,可以根据之前处理的前缀和算出。
这样每个元素就可以在 的时间内求出出现次数,然后就可以愉快的AC
神仙分块黑题了了。 (细节很多,调了很久)Code
#include <iostream> #include <cstdlib> #include <cstdio> #include <cmath> #include <cstring> #include <algorithm> using namespace std; const int N = 40040; const int K = 220; int n, m, L, len, sum[K][N], vis[N]; int tmpnum[N], B[N], last, pre[N]; struct getin { int id, d, se; }a[N]; struct node { int num, s; }p[K][K]; inline bool cmp1(getin x, getin y) { return x.d < y.d; } inline bool cmp2(getin x, getin y) { return x.id < y.id; } inline int getB(int x) { int ret = x / L; if(x % L) ret++; return ret; } inline void prework() { for(int i = 1; i <= len; i++) { memset(B, 0, sizeof(B)); node tmp; tmp.num = tmp.s = 0; for(int j = i; j <= len; j++) { for(int k = (j - 1) * L + 1; k <= min(n, j * L); k++) { B[a[k].se]++; if(B[a[k].se] > tmp.s) { tmp.num = a[k].se; tmp.s = B[a[k].se]; } else if(B[a[k].se] == tmp.s) tmp.num = min(tmp.num, a[k].se), tmp.s = B[a[k].se]; } p[i][j] = tmp; } } for(int i = 1; i <= len; i++) { for(int j = 1; j <= n; j++) sum[i][a[j].se] = sum[i - 1][a[j].se]; for(int j = (i - 1) * L + 1; j <= min(n, i * L); j++) sum[i][a[j].se]++; } } int main() { scanf("%d%d", &n, &m); L = sqrt(n); len = (n + L - 1) / L; for(int i = 1; i <= n; i++) scanf("%d", &a[i].d), a[i].id = i; sort(a + 1, a + n + 1, cmp1); a[0].d = -1; for(int i = 1; i <= n; i++) { a[i].se = a[i - 1].se; if(a[i - 1].d != a[i].d) a[i].se++; pre[a[i].se] = a[i].d; } sort(a + 1, a + n + 1, cmp2); prework(); for(int i = 1; i <= m; i++) { int l, r; scanf("%d%d", &l, &r); l = (l + last - 1) % n + 1; r = (r + last - 1) % n + 1; if(l > r) swap(l, r); int posl = getB(l), posr = getB(r); if(posr - posl <= 2) { int ans = 0; for(int j = l; j <= r; j++) tmpnum[a[j].se] = 0; for(int j = l; j <= r; j++) { tmpnum[a[j].se]++; if(tmpnum[a[j].se] > tmpnum[ans]) ans = a[j].se; else if(tmpnum[a[j].se] == tmpnum[ans]) ans = min(ans, a[j].se); } printf("%d\n", last = pre[ans]); } else { int ans = p[posl + 1][posr - 1].num; tmpnum[ans] = 0, vis[ans] = 0; for(int j = l; j <= min(n, posl * L); j++) tmpnum[a[j].se] = 0, vis[a[j].se] = 0; for(int j = (posr - 1) * L + 1; j <= r; j++) tmpnum[a[j].se] = 0, vis[a[j].se] = 0; for(int j = l; j <= min(n, posl * L); j++) tmpnum[a[j].se]++; for(int j = (posr - 1) * L + 1; j <= r; j++) tmpnum[a[j].se]++; int MXnum, MX = 0; for(int j = l; j <= min(n, posl * L); j++) if(!vis[a[j].se]) { vis[a[j].se] = 1; int val = tmpnum[a[j].se] + sum[posr - 1][a[j].se] - sum[posl][a[j].se]; if(MX < val) MX = val, MXnum = a[j].se; else if(MX == val) MXnum = min(MXnum, a[j].se); } for(int j = (posr - 1) * L + 1; j <= r; j++) if(!vis[a[j].se]) { vis[a[j].se] = 1; int val = tmpnum[a[j].se] + sum[posr - 1][a[j].se] - sum[posl][a[j].se]; if(MX < val) MX = val, MXnum = a[j].se; else if(MX == val) MXnum = min(MXnum, a[j].se); } if(MX > tmpnum[ans] + p[posl + 1][posr - 1].s) ans = MXnum; else if(MX == tmpnum[ans] + p[posl + 1][posr - 1].s) ans = min(ans, MXnum); printf("%d\n", last = pre[ans]); } } return 0; }
- 1
信息
- ID
- 3094
- 时间
- 1000ms
- 内存
- 512MiB
- 难度
- 6
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
