自动搬运

查看原文

来自洛谷，原作者为

	王熙文 **

搬运于2025-08-24 21:56:52，当前版本为作者最后更新于2023-01-04 16:06:07，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

结论简单但是证明巧妙的题，题解区竟然没有一个像样的证明，因此我写一篇题解。

upd at 2023.7.1: 这篇题解是在大规模撤下题解之前写的，我记得之前提交成题解了，但是不知道为什么也被撤了。我感觉这篇题解证明很清楚啊。

思路

结论：当 $n$ 为奇数时后手赢，$n$ 为偶数时先手赢。

证明：

首先将棋盘黑白染色，左上角为黑色。这样先手只会走到白格子，后手只会走到黑格子。将相邻的格子连接。这样形成了二分图。

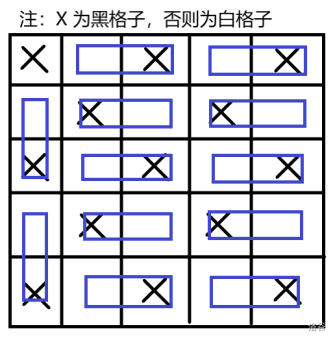
• 当 $n$ 为奇数时：使用一种方式将不是左上角的格子完美匹配。这样当先手走到一个白格子的时候，后手只需要走到完美匹配中对应的黑格子，就每次都能应对了。但是先手每一次都需要新找到没有被访问过的白格子，迟早会找不到的（最差在最后白格子都染完了先手肯定找不到），所以后手赢。构造完美匹配的方法是：将在第一行相邻的左右匹配，第一列相邻的上下匹配，剩下的位置左右匹配即可。比如，这是 $n=5$ 时的完美匹配。

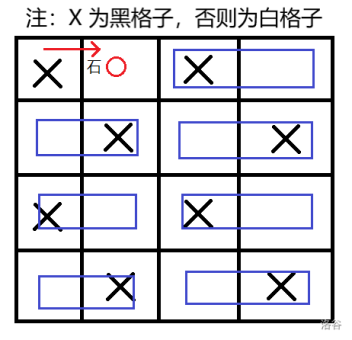
• 当 $n$ 为偶数时：和奇数一样，只不过这次主动权变成了先手。先手先走一步（向下和向右是一样的，所以下面默认向右走），然后使用一种方式将不是左上角和先手走过的格子完美匹配。这样当后手走到一个黑格子里，先手就走到对应的白格子即可。后手迟早会找不到新的，所以先手赢。构造完美匹配的方法是：将每一行相邻的两个左右匹配即可。比如，这是 $n=4$ 时的完美匹配。

代码

#include<bits/stdc++.h>
using namespace std;
int main()
{
    int n;
    while(cin>>n && n) cout<<(n%2==0?"Alice":"Bob")<<'\n';
    return 0;
}