自动搬运

查看原文

来自洛谷，原作者为

	璀璨星空1 倘若我们义无反顾去做不可能之事，世上便再没有不可能。

搬运于2025-08-24 21:56:45，当前版本为作者最后更新于2021-08-21 22:26:13，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

考虑先做第二问，再做第一问.

我们想要构造一种 $n$ 轮均合法的移动操作，将 $n$ 片针叶全部都移走；考虑先移走 1 片，将问题转化为 $n-1$ 片针叶全部都移走，不难发现这是我们必须解决的，而且这样问题只会变简单.

哪 1 片针叶是可以立刻就移走的？比如说我们想要让这片针叶向下直接移走，那么这片针叶下面就不能有任何的阻碍，一个粗糙的想法是直接选择 $y$ 坐标最靠下的那片针叶.

但是这样可能会出问题，如下图所示：

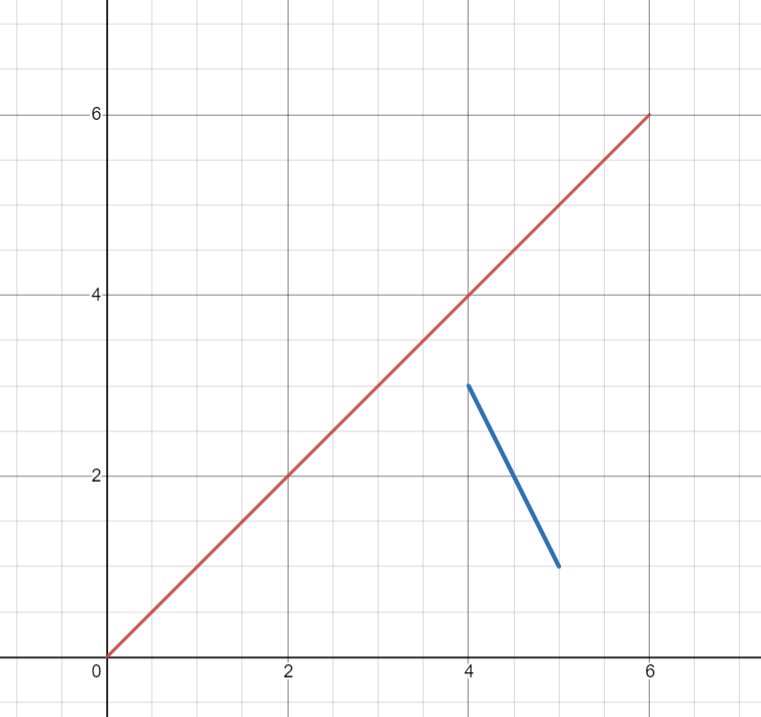
如果我们直接向下移动红色的针叶，会被蓝色的针叶所阻碍.

这启发我们，找到一片没有被任何针叶阻碍的针叶，还是以向下移走为例子，我们看，如果只考虑上下之间的障碍，能否一定能够找到一片，没有被任何针叶阻碍的针叶.

首先，如果针叶 $u$ 阻碍了针叶 $v$，那么不可能反过来，也就是不可能针叶 $v$ 能够阻碍针叶 $u$.

因此，如果对于每个针叶 $i$，都看成一张图上的一个结点 $i$，那么这张图就是一张有向无环图.

比如说对于我们的第一个样例而言，针叶建点，阻碍关系建边，就是这样一张图：

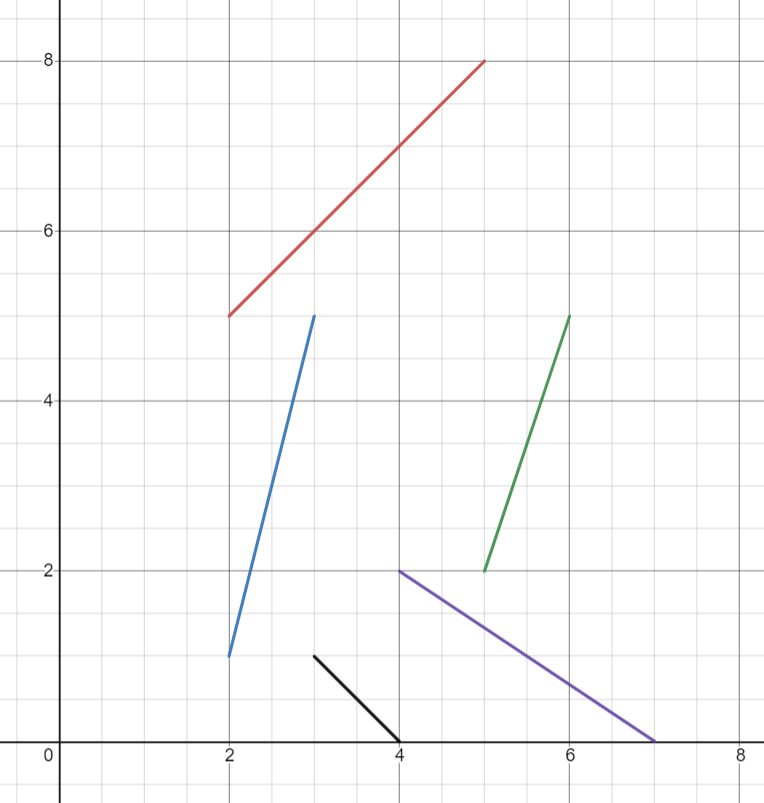
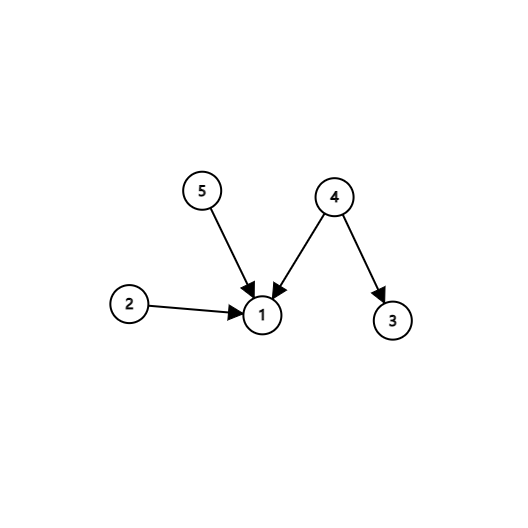
知道了有向无环图有什么用呢？任意一张有向无环图上，一定存在一个结点，没有任何入度.

反证法，如果所有结点都有入度，反图上所有结点就都有出度，此时我们任意选一个点不断走下去，瞎走一通，走到 $n+1$ 步，就一定能找到一个环，这样原图上也就一定能找到一个环.

这样，我们一定能够找到一片针叶 $t$，可以向下直接移走 $t$；重复上述过程 $n$ 步，就说明了一定存在一组合法的解，使得所有的针叶最终都是向下移动的.

这启示我们，如果能够把这张有向无环图真正建出来，它的拓扑序的逆序列就是一个合法的移动序列，按照这个移动序列，一片一片向下移动针叶即可.

直接建图需要枚举 $\mathcal{O}(n^2)$ 条边，不能接受，考虑挖掘为了求出这个图的拓扑序，有什么好的性质.

注意到，如果针叶 $u$ 阻碍了针叶 $x$，针叶 $x$ 又阻碍了针叶 $y$，那么可以直接看作针叶 $u$ 阻碍了针叶 $y$，即使这样的阻碍关系实际上并不存在，

只知道这个性质是没有什么用的，我们并不能刻画出一片针叶 $u$ “恰好” 被哪片针叶所阻碍，又能够 “恰好” 阻碍到哪片针叶.

考虑换一种方式刻画阻碍关系，不再思考点对点贡献，而是直接思考，某个给定的 $x$ 坐标那条直线上，一条平行于 $y$ 轴的直线，会产生什么样的阻碍关系.

假如不考虑边界情况，所有与这条直线有交点的针叶，两两之间都存在阻碍关系.

建图的时候，只要在相邻两片针叶之间，建一条边即可.

如果我们把这条直线稍稍向右移动一些，你可以认为移动了 $\varepsilon$ 的距离，还是不考虑边界情况，没有到达或者跨过整点，那么能建的边和刚才那条直线是完全一样的.

如果移动很多呢？即使跨过了很多整点，只要与这条直线有交点的针叶集合没有变化，能建的边就都不会有变化，回归点对点贡献的思考.

对于两片针叶 $u$ 和 $v$，因为初始状态下两片针叶是无交点的，所以选哪条直线去截它们，能不能连边，连边的方向是什么，只要都截上了，就不会有任何区别.

也就是说，对于某个集合的针叶来说，对于所有能够把它们全截下来的，与 $y$ 轴平行的直线，针叶之间内部连边的序不会有任何变化，哪片针叶在上面就永远会在上面，哪片在下面就永远会在下面.

用一条与 $y$ 轴平行的扫描线，扫过整个平面，$x$ 坐标从 $-\infty$ 扫到 $+\infty$.

假设我们已经处理完了 $x\leq x'$ 的时候，所有直线能建的边，考虑处理 $x=x'+1$.

• 可能会新来一片针叶
  • 需要确定在这片针叶上面的针叶中最靠下的，也就是前驱；再确定在这片针叶上面的针叶中最靠下的，也就是后继，那么新来的针叶阻碍了前驱，后继阻碍了新来的针叶.
  • 用一个 $\texttt{STL Set}$，可以维护所有，与目前扫描线有交点的针叶的编号，新来一片针叶，先在 $\texttt{Set}$ 中查询前驱、后继，之后在 $\texttt{Set}$ 中加入这片针叶即可.
• 可能会有一片针叶消失了
  • 并不需要做什么事情，只要在 $\texttt{Set}$ 中删除这片针叶即可.

如果这样处理，可能会面临一些小问题：

• 如何重定义 $\texttt{Set}$ 的小于号，使得我们可以在不断改变的 $x$ 坐标下比较两条线段的 $y$ 坐标？
  • 利用序不改变的性质，我们可以 ”欺骗“ $\texttt{STL}$：虽然我们传进去的小于号不是严格全序，但是在 $\texttt{STL}$ 的运作周期内，永远都不会发现这一点.
  • 将每条直线用斜截式 $y=kx+b$ 表示，那么 $k$ 和 $b$ 是直线的参数，$x$ 是递增的，$y$ 是需要比较的关键字，之后我们重定义小于号，从某个全局参数处读取此时的 $x$ 进行比较.
    • 这就是说，在扫描线的过程中，每扫到一个有变化的 $x$ 坐标，就微调一下小于号的规则.
  • 因为前面提到的序不变的性质，在 $\texttt{STL}$ 的运作周期内，不可能发现该小于号不是严格全序.
• 如果同一条直线上，又有插入又有删除，该怎么处理？
  • 不难发现，此时要插入的直线和要删除的直线之间，实际上是不能连边的.
    • 对同一个 $x$ 坐标对应的截线，只要一律先处理删除，再处理插入即可.
• 如此，对于每片针叶，我们会在刚扫到这片针叶的时候，让这片针叶连入、连出各不超过 1 条边，这样我们就建出来了，实际阻碍关系图的一张等效图，图上有 $n$ 个结点和不超过 $2n$ 条有向边.

以上是考虑从上到下的阻碍关系建出来的图，我们对这张图作拓扑排序，令针叶 $i$ 在这张图上的拓扑序为 $\alpha_i$，同理，考虑从左到右的阻碍关系，令针叶 $i$ 在那张图上的拓扑序为 $\beta_i$.

对于第一个样例而言，一组可能的 $\alpha$ 和 $\beta$ 分别是 $\{1,4,2,5,3\}$ 和 $\{1,4,2,3,5\}$.

按照拓扑序，将所有针叶向上移动，或者向右移动，可以正确回答所有数据点的第二问，时间复杂度为 $\mathcal{O}(n\log n)$，在第一问上随便输出一个 $1$，就可以获得 $60$ 分的好成绩.

这里要特别注意，实际考试如果遇到这样分步给分的题目，对不想回答的小问，一定要注意什么样的输出是不给分但是可以被接受的；在这道题中，如果第一问随意地输出了 $0$，就会导致第二问的分白白丢掉.

在验证了 $\alpha$ 和 $\beta$ 的正确性之后，就可以考虑如何利用刚才的性质和结论，解决第一问了.

考虑如何判定一步给定的移动操作是不是合法的，这次以向上直接移动为例子.

将一片 $x$ 坐标范围为 $[l,r]$ 的针叶向上移动，假设这片针叶是 $u$，什么样的针叶 $v$ 会对 $u$ 造成阻碍呢？

注意到我们直接在刚才建出来的图上找是不可行的，有这样的一些原因：

• 可能有些针叶 $x$ 能对 $u$ 造成阻碍，但是我们把 $x$ 移走了；
• 如果要处理移走了的针叶，仅仅靠一张等效图是不够的，而原图又没有办法建出来.

这里最大的问题，是我们要试图删除一片针叶，这会破坏这张等效图的等效性.

正难则反，删除操作不可行的时候，考虑逆转时间轴，时间倒流，考虑插入操作.

也就是说，我们从已经被移空了的平面开始，按照操作顺序的倒序，一片一片加入针叶，加入的过程就是从无穷远处移动回原来所在的地方，看哪些针叶会在这个加入的过程中被阻碍.

注意到如果这样做，是不可以剪枝的，必须考虑每一片针叶，因为有可能后来的针叶被阻碍了，前面的针叶也被阻碍，这也就意味着无论一片针叶有没有被阻碍，我们都要在平面上将这片针叶安排回原来的位置，因为这片针叶还有可能去阻碍别人，如果考虑逆转时间轴的实际意义，很容易说明这一点.

既然单从图论的角度难以直接解决问题，我们还是回归移动针叶被阻碍这件事的实际意义.

一片针叶 $v$ 会对 $u$ 造成阻碍，说明 $v$ 的 $x$ 坐标范围 $[l',r']$ 与 $[l,r]$ 是有交的，这里我们将 $v$ 分为两种针叶，分别称作 $\texttt{P}$ 类针叶和 $\texttt{Q}$ 类针叶：

• $\texttt{P}$ 类针叶：$[l',r']$ 包含 $l$ 这个点，或者包含 $r$ 这个点.
• $\texttt{Q}$ 类针叶：$[l',r']$ 是 $[l,r]$ 的中间一段，使得 $l<l'$ 且 $r'<r$.

考虑这些针叶，如何判断这些针叶到底会不会对 $u$ 造成阻碍？这时就要看这些针叶的 $y$ 坐标了，然后我们陷入了和一开始做第二问的时候同样的困境：怎么直接地求出两片针叶之间的阻碍关系呢？

注意到这里考虑到的所有针叶对 $(u,v)$，它们之间一定是存在阻碍关系的，要紧的只是关系的方向，需要知道存不存在 $v$ 阻碍 $u$ 的关系.

既然一定存在阻碍关系，那其实就好办了，还是回归那张等效图.

这时解法基本上已经呼之欲出了，我们不是求出了等效图拓扑序 $\alpha$ 吗，那对于我们已经知道确实存在阻碍关系的针叶对 $(u,v)$，如果 $\alpha_u<\alpha_v$，那就是 $u$ 阻碍 $v$，否则就是 $v$ 阻碍 $u$ 啊.

可能会产生一个疑问：如果直接当作 $\alpha_v$ 去处理的话，两片 $\texttt{Q}$ 类针叶之间的阻碍关系是不是可能会误判呢？但其实这是不要紧的，因为我们根本不关心这些，我们只关心所有的针叶对 $(u,v)$.

所以判断其实很简单：考虑所有坐标范围与 $[l,r]$ 有交的针叶，如果这里面，$\alpha_v$ 的最小值，都大于 $\alpha_u$ 的话，那么全是 $u$ 阻碍 $v$，所以这一步移动 $u$ 的操作一定是可行的，反之，则一定不可行；

需要用数据结构快速维护这个过程，不难想到线段树，具体过程如下：

• 将所有移动操作读入进来离线，逆转时间轴，逆序考虑所有的操作；

  • 当然在这之前，要先离散化所有的坐标，注意离散化是在这一步才进行，而不是在一开始的时候就进行离散化，否则因为斜率等问题会产生错误.

• 建立两棵线段树 $T_x$ 和 $T_y$；

• 设这一步移动操作移动的针叶编号是 $u$，$u$ 的 $x$ 坐标范围是 $[l_x,r_x]$，$y$ 坐标范围是 $[l_y,r_y]$：

  • 设布尔标记 $\texttt{Flag}$ 为真；
  • 如果是操作 $\texttt{0}$，也就是向左移动：
    • 在 $T_y$ 中查询 $[l_y,r_y-1]$ 的区间最大值，如果该值大于 $\beta_u$，就令 $\texttt{Flag}$ 为假；
  • 如果是操作 $\texttt{1}$，也就是向上移动：
    • 在 $T_x$ 中查询 $[l_x,r_x-1]$ 的区间最小值，如果该值小于 $\alpha_u$，就令 $\texttt{Flag}$ 为假；
  • 如果是操作 $\texttt{2}$，也就是向右移动：
    • 在 $T_y$ 中查询 $[l_y,r_y-1]$ 的区间最小值，如果该值小于 $\beta_u$，就令 $\texttt{Flag}$ 为假；
  • 如果是操作 $\texttt{3}$，也就是向下移动：
    • 在 $T_x$ 中查询 $[l_x,r_x-1]$ 的区间最大值，如果该值大于 $\alpha_u$，就令 $\texttt{Flag}$ 为假；
  • 在 $T_x$ 中以 $\alpha_u$ 的值更新区间 $[l_x,r_x-1]$；
  • 在 $T_y$ 中以 $\beta_u$ 的值更新区间 $[l_y,r_y-1]$；
  • 若 $\texttt{Flag}$ 为假，记录目前的操作步骤 $i$ 是不合法的；

最终最早的不合法步骤即为第一问的答案，可以正确回答所有数据点的第一问，时间复杂度为 $\mathcal{O}(n\log n)$，空间复杂度为 $\mathcal{O}(n)$，可以获得这道题的 $100$ 分.

常数主要在线段树上，如果写 zkw 线段树可以降低常数，但是考虑到 3 秒的时间限制，没有必要.

肝了 3.5h，接近 300 行、7.7 个 KB 的代码不得贴一下 qwq.