自动搬运

查看原文

来自洛谷，原作者为

	hehezhou **

搬运于2025-08-24 21:56:39，当前版本为作者最后更新于2019-05-22 15:16:07，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

Qtree4

题意:
$n$个点，每个点有一个颜色，黑或白
每次查询最大白点间距离
带修改
$n=10^5,q=2*10^5$

(相信大家边分治，LCT等 $O(nlog^2n)$做法都会了)

但是这里有一个常数巨大的$O(nlogn)$做法

前置芝士

1.全局平衡二叉树(详见2007年论文Qtree问题解法的一些研究)

在一些静态树上查询，修改问题中，LCT能做到超大常数的$O(logn)$,而树链剖分只能做到$O(log^2n)$，原因何在?

因为LCT整棵树可以看做一个大的spaly$splay$，仍然可以进行势能分析
而树剖只能做到单条链最优(局部最优)，但是全局并没有最优

全局平衡二叉树 就完成了把LCT强行静态的过程

轻重链剖分的部分是一样的，但是我们对每一条链建立一颗二叉搜索树
给每一个点一个权值为轻儿子$size$之和$+1$(自己)，然后每次找重心递归建树

证明每个点的深度为$O(logn)$很简单，每次调到父亲子树大小(包括虚子树)至少翻倍

然后就可以开开心心的以一个$log$的做法做树剖题了

2.把任意一棵树转化为树上距离不变的二叉树

相信大家都学过边分治吧，那我就不讲了

直接上图

原树

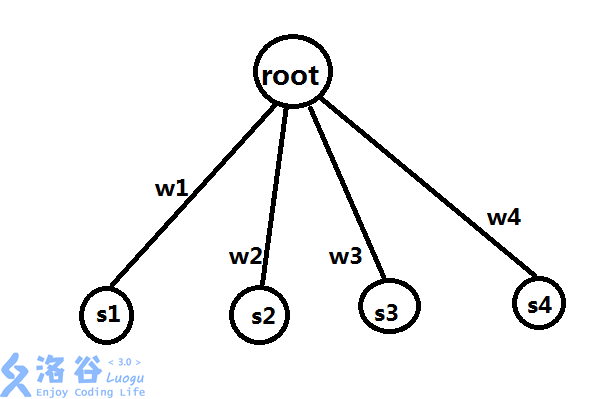
二叉树

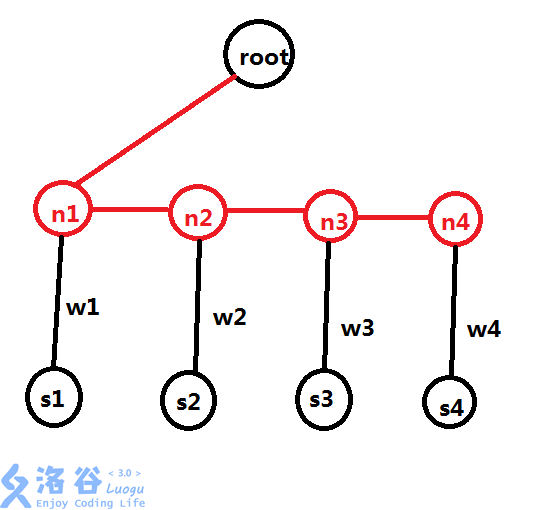
其中红点为新建的虚点，红边的边权均为0
对于每一个点，它的儿子都这样处理，然后就变成有$2n$个点的二叉树了
感受一下，是不是很神奇?

---

正题开始

首先考虑最强的树上分治链分治
对于每一条链维护$lca$在这条链上的最大白点距离
直接做的做法:

以下为了方便，点$x$的轻子树和表示以$x$为根的子树去掉它的重子树，点$x$的轻子树表示以它的一个轻儿子为根的子树，$dfn$表示$dfs$序

对于每一个点$x$维护一个堆，记录$x$的每个轻子树内任意黑点到$x$的距离的最大值，

线段树维护答案
对于$dfn$区间$[l,r]$,记录三个值:
1.$lmax$:所有$dfn$为$[l,r]$点的轻子树和内的所有黑点到$dfn$为$l$的点的距离最大值
2.$rmax$:同理，表示所有$dfn$为$[l,r]$点的轻子树和内的所有黑点到$dfn$为$l$的点的距离最大值
3.$ans$:表示所有$dfn[lca]\in [l,r]$ 的黑点的距离最大值

区间合并:线段树上$x$的左儿子为$ls$，右儿子为$rs$

$$ans_x=max\{ans_{ls},ans_{rs},rmax_{ls}+lmax_{rs}+dis(r_{ls},l_{rs})\} $$$$lmax_x=max\{lmax_{ls},lmax_{rs}+dist(l_{ls},l_{rs})\} $$$$rmax_x=max\{rmax_{rs},rmax_{ls}+dist(r_{ls},r_{rs})\} $$

边界:点$x$对应区间$[L,L]$ $D_1=$堆内的最大值，$D_2=$堆内的次大值(来自两个不同轻子树)(若没有为$-\infty$)

若$x$为白点

$$lmax_x=rmax_x=max\{0,D_1\}$$ $$ans_x=max(0,D_1,D_1+D_2)$$

(自己到自己，自己到最远的，最远的到次远的)
否则

$$lmax_x=rmax_x=D_1$$ $$ans_x=D_1+D_2$$

然后我们发现其实距离堆内维护的就是每个轻儿子线段树顶的$lmax+dist(x,son)$

每条链的答案可以记在另一个堆里，询问时直接查即可

复杂度分析:

dist(i,j):发现总是在求祖先-后代距离，所以深度减一下$O(1)$
建树O(n)
每次修改$O(logn)$条链，每次线段树$O(logn)$,修改距离堆$O(logn)$，修改记答案的堆$O(logn)$总复杂度$O(nlog^2n)$
每次查询$O(1)$获取堆顶即可
总复杂度$O(qlog^2n+n)$

愚蠢的$log^2$做法到此结束

---

考虑降为一个$log$

首先直接上全局平衡二叉树可以把线段树部分降为单次询问$O(logn)$
答案堆直接不要了，全局平衡二叉树的$ans$带上轻子树和内的答案即可

然后是距离堆
我们发现距离堆内的点的个数为轻儿子个数
所以把它转成二叉树就不用堆来维护了

惊不惊喜，意不意外

然后就可以一个$log$愉快的过掉了

其实bb了这么一大堆，代码十分好写

码风丑，大佬轻喷

另外有一个细节，我的二叉查找树结合了线段树的特点，(有点像宗法树)

#pragma GCC optimize(3)
#include <bits/stdc++.h>
using namespace std;
const int inf = 1000000000;
char buf[1 << 20];
char *S = buf, *T = buf;
inline char gc() {
    if(S == T) T = buf + fread(buf, 1, 1 << 20, stdin), S = buf;
    return S == T ? EOF : *S ++;
}
inline int read() {
    int f = 1, c;
    unsigned a = 0;
    for(c = gc(); c != '-' && (c < '0' || c > '9'); c = gc());
    if(c == '-') c = gc(), f = -1;
    for(; c <= '9' && c >= '0'; c = gc()) a = (a << 1) + (a << 3) + (c ^ '0');
    return f == 1 ? a : (~a) + 1;
} // 快速读入
int size[200010], wson[200010], lson[200010], lsize[200010], dep[200010];
struct node {
    int ls, rs, ans, L, R, lmax, rmax, fa;
} t[400010]; //二叉查找树结构体
int nowcnt;
int st[200010], cnt;//记录当前链
int n, m;
vector<pair<int, int> > son[100010];//记录原树
inline void addedge(int u, int v) {
    if(wson[u] == 0) wson[u] = v;
    else lson[u] = v;
}
inline void dfs(int now, int f) {//建立新树
    addedge(now + n, now);
    for(int i = 0; i < son[now].size(); i++)
        if(son[now][i].first == f) {
            son[now].erase(son[now].begin() + i);
            break;
        }
    for(int i = 0; i < son[now].size(); i++) dep[son[now][i].first + n] = dep[now], dep[son[now][i].first] = dep[now] + son[now][i].second, dfs(son[now][i].first, now);//其实此时dep已经可以求出
    for(int i = 1; i < son[now].size(); i++) addedge(son[now][i - 1].first + n, son[now][i].first + n);
    if(son[now].size()) addedge(now, son[now][0].first + n);
}
inline void dfs1(int now) {//树剖的第一次dfs
    size[now] = 1;
    if(wson[now]) dfs1(wson[now]), size[now] += size[wson[now]];
    if(lson[now]) dfs1(lson[now]), size[now] += size[lson[now]];
    if(size[lson[now]] > size[wson[now]]) swap(lson[now], wson[now]);
    lsize[now] = size[lson[now]] + 1; 
}
inline int build(int l, int r) {//对st[l...r]建立二叉树
    if(l == r) return t[st[l]].L = t[st[l]].R = st[l]; //此处有压行(逃)
    int sum = 0, cnt = 0, ans;
    for(int i = l; i <= r; i++) sum += lsize[st[i]];
    sum >>= 1;
    for(int i = l; i <= r; i++) {
        cnt += lsize[st[i]];
        if(cnt >= sum) {//找到重心
            if(i == l) i++;//要是不加，哼哼
            ans = ++nowcnt;
            t[ans].ls = build(l, i - 1);
            t[ans].rs = build(i, r);
            t[t[ans].ls].fa = t[t[ans].rs].fa = ans;
            t[ans].L = st[l], t[ans].R = st[r];
            return ans;
        }
    }
}
int root;
inline void dfs2(int now) {
//st[1...cnt]保存当前链，st[0]为链头的父亲(为0则链头为根)
    st[++cnt] = now;
    if(wson[now]) dfs2(wson[now]);
    else {
        int rt = build(1, cnt);
        if(st[0] == 0) root = rt;
        else t[rt].fa = st[0], t[st[0]].ls = t[st[0]].rs = rt;
        cnt = 0;
    }
    st[0] = now;
    if(lson[now]) dfs2(lson[now]);
}
int col[200010];
inline void up(int x) {
    node &now = t[x];
    if(now.L == now.R) {//叶子节点
        int D = t[now.ls].lmax + dep[lson[x]] - dep[x];//因为是二叉树，所以不会有D2
        now.ans = t[now.ls].ans;
        if(col[x]) now.ans = max(now.ans, now.lmax = now.rmax = max(D, 0));
        else now.lmax = now.rmax = D;
    }
    else {//非叶子节点
        now.lmax = max(t[now.ls].lmax, t[now.rs].lmax + dep[t[now.rs].L] - dep[now.L]);
        now.rmax = max(t[now.rs].rmax, t[now.ls].rmax + dep[now.R] - dep[t[now.ls].R]);
        now.ans = max(max(t[now.ls].ans, t[now.rs].ans), t[now.ls].rmax + t[now.rs].lmax + dep[t[now.rs].L] - dep[t[now.ls].R]);
    }
}
inline void init(int now) {
    if(t[now].L == t[now].R) {
        if(t[now].ls) init(t[now].ls);
    }
    else init(t[now].ls), init(t[now].rs);
    up(now);
}
int main() {
    // freopen("hehezhou.in", "r", stdin);
    // freopen("hehezhou.out", "w", stdout);
    t[0].lmax = t[0].ans = t[0].rmax = -inf;
    n = read();
    for(int i = 1, u, v, w; i < n; i++) u = read(), v = read(), w = read(), son[u].push_back(make_pair(v, w)), son[v].push_back(make_pair(u, w));
    dfs(1, 0);
    nowcnt = n << 1;
    dfs1(n + 1);
    dfs2(n + 1);
    // for(int i = 1; i <= n << 1; i++) printf("%d %d\n", wson[i], lson[i]);
    for(int i = 1; i <= n; i++) col[i] = 1;
    // for(int i = 1; i <= nowcnt; i++) printf("%d : ls = % d, rs = %d, fa = %d, L = %d, R = %d\n", i, t[i].ls, t[i].rs, t[i].fa, t[i].L, t[i].R);
    init(root);
    nowcnt = n;//在这之前表示二叉搜索树节点当前使用量，之后表示白点个数
    m = read();
    for(int i = 1; i <= m; i++) {
        char opt;
        for(opt = gc(); opt != 'C' && opt != 'A'; opt = gc());
        if(opt == 'A') nowcnt ? printf("%d\n", t[root].ans) : puts("They have disappeared.");
        else {
            int v;
            v = read();
            if((col[v] ^= 1) == 0) nowcnt--;//压行大法好
            else nowcnt++;
            for(; v; v = t[v].fa) up(v);
        }
    }
    return 0;//完结撒花
}

最后祝大家$rp$++