自动搬运

查看原文

来自洛谷，原作者为

	zhy137036 AFO

搬运于2025-08-24 21:56:36，当前版本为作者最后更新于2021-01-25 15:07:50，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

作为 OI-Wiki 上矩阵树定理的例题，这道题似乎没有详细讲矩阵树定理的题解，而且 OI-Wiki 讲得十分晦涩。

首先这道题容易转化为：已知无向图，求它的生成树数量。这正是矩阵树定理的作用。

矩阵树定理

拉普拉斯矩阵

设无向图有 $n$ 个节点。拉普拉斯矩阵 $L$ 是一个 $n\times n$ 的矩阵。定义如下：

• $L_{i,i}$ 的值为节点 $i$ 的度数，即有多少条边和节点 $i$ 相连。
• $L_{i,j}\ (i\neq j)$ 的值为节点 $i$ 和节点 $j$ 之间相连的边数的相反数。

例如下图：

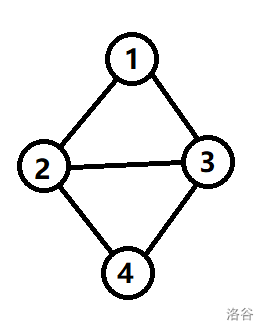
我们发现有两条边和节点 $1$ 相连，有三条边和节点 $2$ 相连，有三条边和节点 $3$ 相连，有两条边和节点 $4$ 相连，所以这个图各个节点的度数 $\deg=\{2,3,3,2\}$。

暂时写成如下矩阵：

$$\begin{bmatrix}2&0&0&0\\0&3&0&0\\0&0&3&0\\0&0&0&2\end{bmatrix} $$

然后对于每条边 $(i,j)$，我们令 $L_{i,j}=L_{j,i}=-1$，得到最终的拉普拉斯矩阵：

$$L=\begin{bmatrix}2&-1&-1&0\\-1&3&-1&-1\\-1&-1&3&-1\\0&-1&-1&2\end{bmatrix} $$

定理叙述

将拉普拉斯矩阵去掉任意的一行和一列，得到的矩阵求行列式，即是原图的生成树数量。

例如将刚才的矩阵去掉最后一行和最后一列，得到：

$$\begin{bmatrix}2&-1&-1\\-1&3&-1\\-1&-1&3\end{bmatrix} $$

计算这个矩阵的行列式。如果不会算，可以用在线计算器。

该矩阵的行列式为 $8$，意思是说原图有 $8$ 个生成树。验证一下，发现原图确实有 $8$ 个生成树，如下：

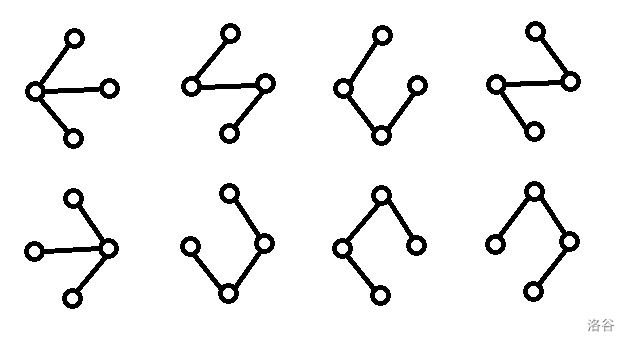
证明就算了，不会证。

行列式

如何求一个矩阵的行列式呢？我们需要知道行列式的一些性质：

• 将矩阵的两行交换，其行列式变成相反数。
• 将矩阵的一行加上(另一行乘一个数)，其行列式不变。
• 三角矩阵的行列式为对角线的乘积。

后两条不是很理解没关系，我们来求一下刚才那个矩阵的行列式。

将第一行乘 $\dfrac12$，加到第二行和第三行上去：

$$\begin{vmatrix}2&-1&-1\\-1+2\times\dfrac12&3+(-1)\times\dfrac12&-1+(-1)\times\dfrac12\\-1+2\times\dfrac12&-1+(-1)\times\dfrac12&3+(-1)\times\dfrac12\end{vmatrix}=\begin{vmatrix}2&-1&-1\\0&\dfrac52&-\dfrac32\\0&-\dfrac32&\dfrac52\end{vmatrix} $$

再将第二行乘 $\dfrac35$，加到第三行上去：

$$=\begin{vmatrix}2&-1&-1\\0&\dfrac52&-\dfrac32\\0+0\times\dfrac35&-\dfrac32+\dfrac{5}2\times\dfrac35&\dfrac52+(-\dfrac32)\times\dfrac35\end{vmatrix}=\begin{vmatrix}2&-1&-1\\0&\dfrac52&-\dfrac32\\0&0&\dfrac85\end{vmatrix} $$

我们看最后得到的矩阵，它只有右上的一个三角形内有数，所以我们称它为“三角矩阵”。将它的对角线乘起来：$2\times\dfrac52\times\dfrac85=8$，就是原矩阵的行列式。

我们发现，这其实就是高斯消元法（不知道高斯消元法也没关系）。但是其中用到了分数，如果模数是质数可以用乘法逆元，否则因为分数在计算机上会有浮点误差，所以我们需要结合没有浮点误差的辗转相除法使用。

我们以较简单的二阶行列式为例：

$$\begin{vmatrix}7&2\\3&5\end{vmatrix}$$

用第二行去消第一行，也就是将第一行不断地减第二行，直到不能继续减，得到：

$$=\begin{vmatrix}1&-8\\3&5\end{vmatrix}$$

然后交换两行，继续消：

$$=-\begin{vmatrix}3&5\\1&-8\end{vmatrix}$$ $$=-\begin{vmatrix}0&29\\1&-8\end{vmatrix}$$ $$=\begin{vmatrix}1&-8\\0&29\end{vmatrix}$$

（注意前面的符号）

于是我们就将这个矩阵变成了三角矩阵。

如果是更多阶行列式，就需要用高斯消元法来逐个消去左下的数，使之成为三角矩阵。

推广

如果原图是有边权的，那又会怎样呢？

这时定义一个节点的度数为 和它相连的边 的边权和，$L_{i,j}\ (i\neq j)$ 的值为边 $(i,j)$ 的边权的相反数。

这时求出的值为所有生成树的(包含的所有边的乘积)的和，即：

$$\sum_{T\text{ 为原图的生成树}}\quad\prod_{e\text{ 为 }T\text{ 中的边}}w_e $$

代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
char ch[20][20];//读入的地图
const int mod=1000000000;
int n,m,cnt,ans=1,id[20][20],A[100][100];
//A 是拉普拉斯矩阵，id 是地图中的格子的编号
void add(int x,int y) { A[x][y]--; A[y][x]--; A[x][x]++; A[y][y]++; }
//对于一个边，修改拉普拉斯矩阵
signed main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) cin>>ch[i][j];
	for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) if(ch[i][j]=='.') id[i][j]=++cnt;
    //将地图中的格子进行编号
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++){
			if(ch[i][j]=='.'&&ch[i+1][j]=='.') add(id[i][j],id[i+1][j]);
			if(ch[i][j]=='.'&&ch[i][j+1]=='.') add(id[i][j],id[i][j+1]);
            //只加向下的边和向右的边，防止重复
		}
	cnt--;//去掉拉普拉斯矩阵的最后一行一列
	for(int i=1;i<cnt;i++){
		for(int j=i+1;j<=cnt;j++){
			while(A[j][i]){
				int l=A[i][i]/A[j][i];
                //这里不能直接取模，要先计算商
				for(int k=1;k<=cnt;k++)
					A[i][k]=(A[i][k]-A[j][k]*l%mod+mod)%mod;
				for(int k=1;k<=cnt;k++) swap(A[i][k],A[j][k]);
				ans*=-1;
                //每次交换两行，将答案取相反数
			}
		}
	}
	for(int i=1;i<=cnt;i++) ans=(ans*A[i][i]%mod+mod)%mod;
	cout<<ans<<endl;
	return 0;
}