自动搬运

查看原文

来自洛谷，原作者为

	CG__HeavenHealer 年月把擁有變作失去，疲倦的雙眼帶著期望

搬运于2025-08-24 21:56:33，当前版本为作者最后更新于2021-06-23 17:35:13，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

【题解】 P4104 [HEOI2014]平衡

题意：

有 $1$ 到 $2n+1$ 的一个杠杆，支点在 $n +1$ 处，起初每个刻度上都有一个质量相同的钩码，问拿走 $k$ 个钩码使杠杆仍保持平衡的方案数。

解法：

前置知识：

1. 杠杆的平衡条件： $F_1l_1 = F_2l_2$ ， 左边的重心到支点的距离等于右边中心到支点的距离
2. 整数划分

另：关于整数划分（会的请自行跳过）

整数划分是求解一类诸如用 $k$ 个整数的和表示一个数 $n$ 的方案的问题，解法是DP。

对于每一个数的拆分方式，我们可以分为两种：

1. 表示这个数的几个数中，最小值为 $1$ 。
2. 表示这个数的几个数中，最小值不为 $1$ 。

设 $f[i][j]$ 为：用 $j$ 个数拆分 $i$ 这个数的方案数（这 $j$ 个数之间可以重复），那么对于以上两种情况，怎么实现转移呢？

对于1，它可以由 $f[i][j]$ 表示出 $f[i + 1][j + 1]$ 的状态，理由就是对每个 $i$ 的方案，我们都可以加一个 $1$ 使其成为 $i+1$ 的一种方案；

而对于2，它可以由 $f[i][j]$ 表示出 $f[i + j][j]$ 的状态，理由就是对每个 $i$ 的方案，我们可以在每一个数上加一个 $1$ 使其成为 $i+j$ 的一种方案；

下面附上两种情况的解释：

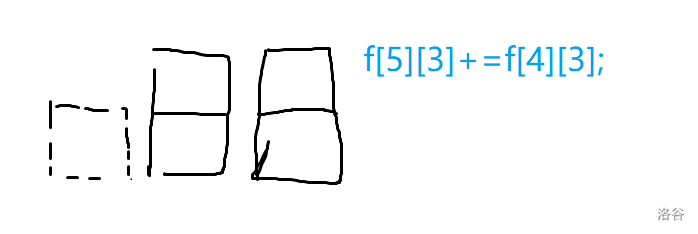
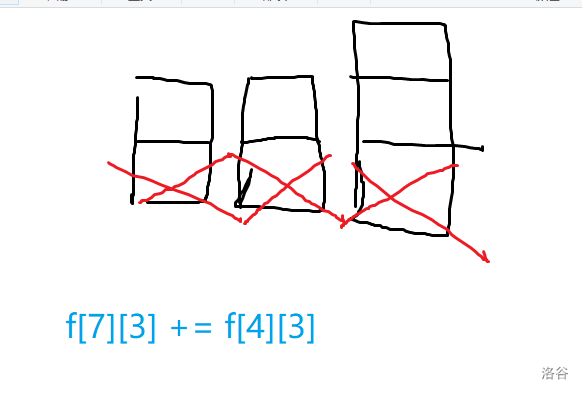
那么，转移方程就是： $f[i][j]=f[i-1][j-1]+f[i-j][j]$。

（可以左转切掉 这里 的例题 ）

言归正传，回到这道题：

对于1，因为钩码的质量都相等，所以对于每一侧，其重心都是成一个对称的效果。

而2又用在哪里呢？

我们设取出的数字之和为 $x$ ，那么解答等价于求出 $x = (n+1) \times k$ 的方案数。

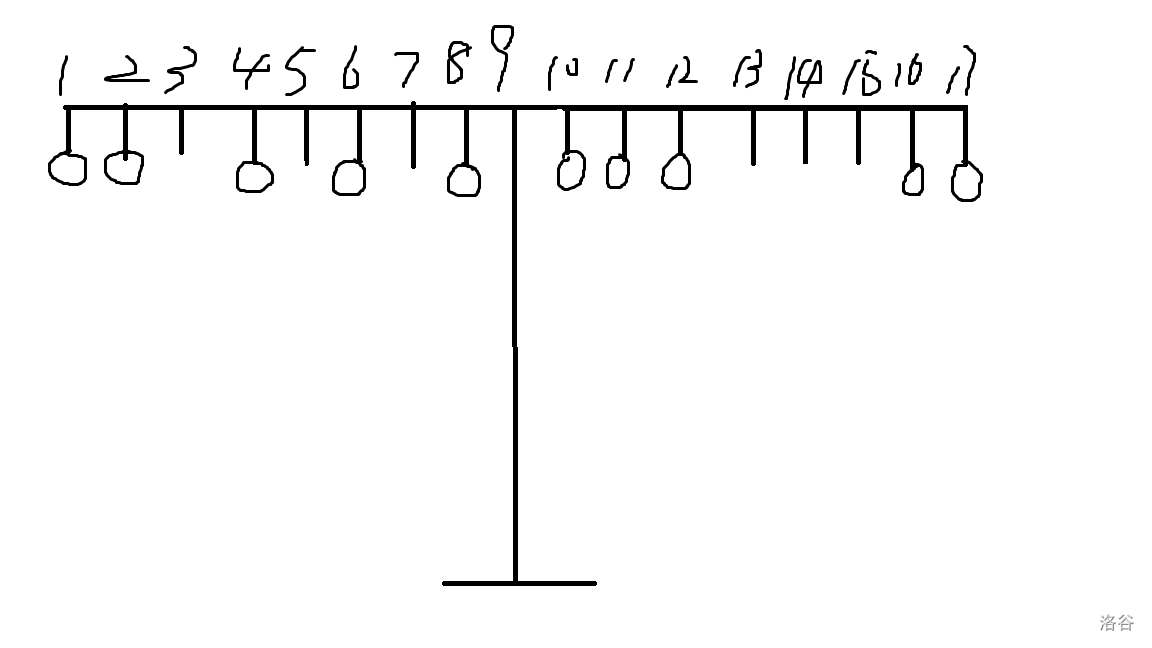
如图，类似于这样的杠杆都是平衡的。

类似于整数划分，我们可以设 $f[i][j]$ 为用 $j$ 个数拆分 $i$ 这个数的方案数（这 $j$ 个数之间不能重复），同样的，对于每一个数的拆分方式，我们可以分为最小值为 $1$ 和不为 $1$ 的两种，转移分别是：

1. 最小值为 $1$ ：$f[i][j]$ 可以从 $f[i-j][j-1]$ 转移过来（因为已知这几个数之间不能重复，那么最小值为1，这几个数中就肯定只有一个1，我们可以给每个数都减掉一个1，剩下的是 $j-1$ 个数，这样就可以从 $f[i-j][j-1]$ 这个状态转移到 $f[i][j]$ 了。)
2. 最小值不为 $1$ ：$f[i][j]$ 可以从 $f[i-j][j]$ 转移过来，理由和有重复的划分相同。

则转移方程为： $f[i][j]=f[i-j][j-1]+f[i-j][j]$ ，最后答案为 $f[(n+1) \times k][k]$ 。

剩下要注意的事情就是要注意处理边界，因为我们要处理出 $k$ 个数的和为 $(n+1)\times k$ 的方案数，而杠杆长度只有 $2\times n +1$ ，所以有些方案是不合法的，需要减掉。

Code：

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define ri register int
const int N = 1e4 + 5, K = 15;
int n, k, p, f[N * K * 2][K]; // f[i][j]表示用j个数表示i的方案数
inline int read() {
    ri x = 0, f = 1;
    char ch = getchar();
    for (; !isdigit(ch); ch = getchar())
        if (ch == '-') f = -1;
    for (; isdigit(ch); ch = getchar()) x = (x << 1) + (x << 3) + (ch ^ 48);
    return f * x;
}
signed main() {
    for (ri T = read(); T--; memset(f, 0, sizeof(f))) {
        n = read(), k = read(), p = read();
        f[0][0] = 1;
        for (ri i = 1; i <= (n + 1) * k; i++)
            for (ri j = 1; j <= k; j++) {
                if (i < j) continue;
                f[i][j] = (f[i - j][j] + f[i - j][j - 1]) % p; // 整数划分
                if (i >= (n + 1) * 2) // 注意处理超出杠杆的部分，要减去i-(n+1)*2的方案数
                    ((f[i][j] -= f[i - (n + 1) * 2][j - 1]) += p) %= p;
            }
        printf("%lld\n", (f[(n + 1) * k][k] + p) % p);
    }
    return 0;
}