自动搬运

查看原文

来自洛谷，原作者为

	guyan **

搬运于2025-08-24 21:56:15，当前版本为作者最后更新于2020-03-02 19:54:03，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

按限制模拟 , 只有三种行走方式 :

1. 沿边界走

2. 在左上 , 右下徘徊

3. 上下或左右反复

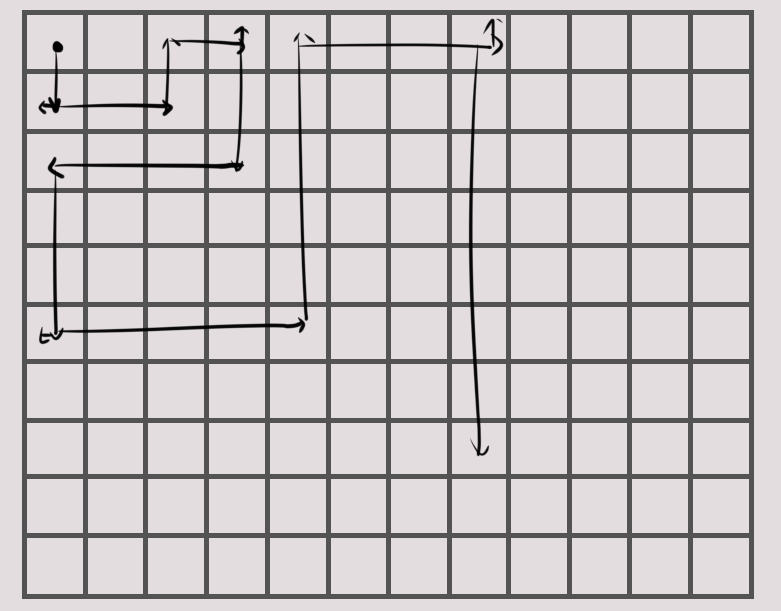
于是可以分为三个阶段 , 在起点徘徊 , 上下/左右 , 在终点徘徊

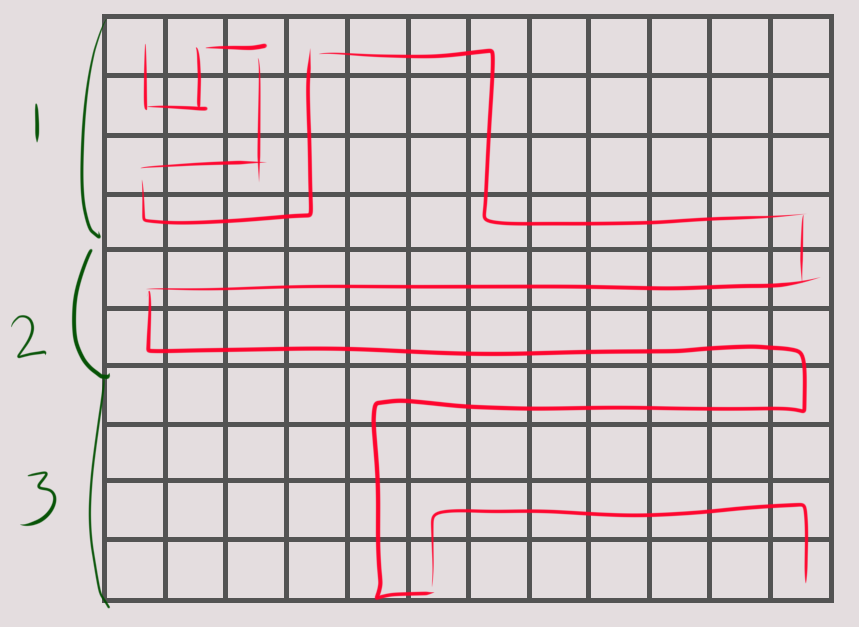
上下走就是转置后左右走

在起点徘徊和在终点徘徊中心对称翻转

于是只用考虑两个 DP , 第一个在角落徘徊 , 第二个左右来回

设 $f[i][j]$ 表示在 $(1,j)$ , 最多走到第 $i$ 行的最大收益 , $g[i][j]$ 表示在 $(i,1)$ , 最多走到第 $j$ 列的最大收益

于是有转移

$f[i][j] = \max( f[i][j - 1] + a_{1,j} , f[i - 1][j] , g[i - 1][j - 1] + profit_{(i,1) \rightarrow (i,j) \rightarrow (1,j) })$

$g[i][j] = \max( g[i - 1][j] + a_{i,1} , g[i][j - 1] , f[i - 1][j - 1] + profit_{(1,j) \rightarrow (i,j) \rightarrow (i,1) })$

于是可以得到到达 $(i,1) , (i,m)$ 的最大收益 , 第一个 DP 就完成了

设 $h[i][0/1]$ 表示在 $(i,1),(i,m)$ 时的最大收益

$h[i][0] = \max( h[i - 1][0] + a_{i,1} , h[k][1] + profit_{(k,m)\rightarrow (i,m) \rightarrow (i,1)} ) ( k < i)$

$h[i][1] = \max( h[i - 1][1] + a_{i,1} , h[k][0] + profit_{(k,1)\rightarrow (i,m) \rightarrow (i,m)} ) (k < i)$

最后与在 $(n,m)$ 徘徊的 DP 合并求一下答案就可以了

#include <bits/stdc++.h>

using namespace std;

typedef long long lol;
const int N = 8e2 + 5;
const lol INF = 1e15;
inline void chkmax( lol & a , lol b ) { if( a < b ) a = b; }
int _w;

int org[N][N] , dat[N][N] , n , m
lol col[N][N] , row[N][N] , L[N] , R[N] , up[N][2] , dn[N][2] , ans = -INF , trs[N] , f[N][N][2];

void calc( void ) { // 计算在边角徘徊
  for( int i = 1 ; i <= n ; ++i )
    for( int j = 1 ; j <= m ; ++j )
      col[i][j] = col[i - 1][j] + dat[i][j] , 
      row[i][j] = row[i][j - 1] + dat[i][j];
  for( int i = 1 ; i <= n ; ++i )
    for( int j = 1 ; j <= m ; ++j )
      f[i][j][0] = f[i][j][1] = -INF;
  for( int i = 1 ; i <= n ; ++i ) f[i][1][1] = col[i][1] , f[i][1][0] = dat[1][1];
  for( int i = 1 ; i <= m ; ++i ) f[1][i][1] = dat[1][1] , f[1][i][0] = row[1][i];
  for( int i = 2 ; i <= n ; ++i ) {
    for( int j = 2 ; j <= m ; ++j ) {
      chkmax( f[i][j][0] , f[i - 1][j][0] );
      chkmax( f[i][j][0] , f[i - 1][j - 1][1] + col[i][j] + row[i][j] - dat[i][j] );
      chkmax( f[i][j][0] , f[i][j - 1][0] + dat[1][j] );
      chkmax( f[i][j][1] , f[i][j - 1][1] );
      chkmax( f[i][j][1] , f[i - 1][j - 1][0] + col[i][j] + row[i][j] - dat[i][j] );
      chkmax( f[i][j][1] , f[i - 1][j][1] + dat[i][1] );
    }
  }
  for( int i = 1 ; i <= n ; ++i ) L[i] = R[i] = -INF;
  for( int i = 1 ; i <= n ; ++i )
    for( int j = 1 ; j <= m ; ++j )
      chkmax( L[i] , f[i][j][1] );
  for( int i = 1 ; i <= m ; ++i ) trs[i] = row[1][m] - row[1][i];
  R[1] = row[1][m];
  for( int i = 2 ; i <= n ; ++i )
    for( int j = 1 ; j < m ; ++j ) {
      trs[j] = max( trs[j] + dat[i][m] , col[i][j + 1] + row[i][m] - row[i][j + 1] );
      chkmax( R[i] , f[i][j][0] + trs[j] );
    }
}

void solve( void ) {
  memcpy( dat , org , sizeof dat ); calc();
  for( int i = 1 ; i <= n ; ++i ) up[i][0] = L[i] , up[i][1] = R[i];
  for( int i = 1 ; i <= n ; ++i )
    for( int j = 1 ; j <= m ; ++j )
      dat[i][j] = org[n - i + 1][m - j + 1];
  calc(); for( int i = 1 ; i <= n ; ++i ) dn[i][0] = R[n - i + 1] , dn[i][1] = L[n - i + 1];
  memcpy( dat , org , sizeof dat );
  for( int i = 1 ; i <= n ; ++i )
    for( int j = 1 ; j <= m ; ++j )
      col[i][j] = col[i - 1][j] + dat[i][j] , 
      row[i][j] = row[i][j - 1] + dat[i][j];
  lol l = 0 , r = row[1][m - 1];
  for( int i = 2 ; i <= n ; ++i ) {
    chkmax( up[i][0] , l + col[i][1] );
    chkmax( up[i][1] , r + col[i][m] );
    chkmax( up[i][0] , r + col[i][m] + row[i][m] - dat[i][m] );
    chkmax( up[i][1] , l + col[i][1] + row[i][m] - dat[i][1] );
    chkmax( l , up[i][0] - col[i][1] );
    chkmax( r , up[i][1] - col[i][m] );
  }
  l = row[n][m] , r = dat[n][m];
  chkmax( ans , dn[1][0] );
  chkmax( ans , up[n][1] );
  for( int i = n - 1 ; i > 1 ; --i ) {
    l = max( l + dat[i][1] , dn[i][0] );
    r = max( r + dat[i][m] , dn[i][1] );
    chkmax( ans , l + up[i - 1][0] );
    chkmax( ans , r + up[i - 1][1] );
  }
}

int main( void ) {
  _w = scanf("%d%d",&n,&m);
  for( int i = 1 ; i <= n ; ++i )
    for( int j = 1 ; j <= m ; ++j )
      _w = scanf("%d",org[i] + j );
  solve();
  for( int i = 1 ; i <= n ; ++i )
    for( int j = i + 1 ; j <= m ; ++j )
      swap( org[i][j] , org[j][i] );
  swap( n , m );
  solve();
  cout << ans;
  return 0;
}