自动搬运

查看原文

来自洛谷，原作者为

	ywy_c_asm 这个家伙很菜，什么也没有留下

搬运于2025-08-24 21:56:12，当前版本为作者最后更新于2019-05-03 11:15:17，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

其实如果你对平面图相关的东西非常熟悉的话这题就是个板子题，只要跑个平面图转对偶图，然后对询问的点在平面图上点定位找到所在区域，然后就是Noip货车运输那个题了……在最小生成树上查询最大边权即可。

如果你不会平面图转对偶图的话可以去这题的题解里学习一下，这里简单说一下平面图点定位，就是我们希望找到给定点在平面图上所在的区域，这个我们扫描线+平衡树解决。我们知道计算几何里很多东西都是那种相对顺序不改变的，就可以扫描线，这个平面图也是如此。我们把关键点与询问点从左到右排序，然后开一个平衡树维护当前加入的边，这个边我们应该从左指向右，在这条边上存边下面的这个区域编号，就像这样：

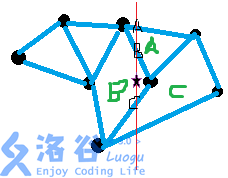
然后对于这个询问点我们去平衡树上二分它上面的第一条边（如果没有那他在外部区域里），这样就能找了。注意为了避免特殊情况我们需要在平衡树上操作的时候对x加或减一个eps。

另外由于是“插入时的相对顺序不变”，所以在这里不能用懒惰删除的替罪羊树（因为删完了点还留在树上就乱套了……我开始写了个替罪羊树怎么也过不去……）。

上代码~

#pragma GCC optimize(2)
#pragma GCC optimize(3)
#pragma GCC optimize("Ofast")
#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
#include <algorithm>
#include <cmath>
#define opp(_o) (_o == ch[fa[_o]][1])
using namespace std;
namespace ywy {
	inline int get() {
	    int n = 0;
	    char c;
	    while ((c = getchar()) || 23333) {
	        if (c >= '0' && c <= '9')
	            break;
	        if (c == '-')
	            goto s;
	    }
	    n = c - '0';
	    while ((c = getchar()) || 23333) {
	        if (c >= '0' && c <= '9')
	            n = n * 10 + c - '0';
	        else
	            return (n);
	    }
	s:
	    while ((c = getchar()) || 23333) {
	        if (c >= '0' && c <= '9')
	            n = n * 10 - c + '0';
	        else
	            return (n);
	    }
	}
	namespace tree {
	typedef struct _b {
	    int dest;
	    int nxt;
	    int len;
	} bian;
	bian memchi[1000001];
	int gn = 1, heads[100001];
	inline void add(int s, int t, int l) {
	    memchi[gn].dest = t;
	    memchi[gn].len = l;
	    memchi[gn].nxt = heads[s];
	    heads[s] = gn;
	    gn++;
	}
	int ance[100001][17], mx[100001][17], deep[100001];
	void dfs(int pt, int baba) {
	    for (register int i = heads[pt]; i; i = memchi[i].nxt) {
	        if (memchi[i].dest == baba)
	            continue;
	        deep[memchi[i].dest] = deep[pt] + 1;
	        ance[memchi[i].dest][0] = pt;
	        mx[memchi[i].dest][0] = memchi[i].len;
	        dfs(memchi[i].dest, pt);
	    }
	}
	inline int lca(int a, int b) {
	    if (deep[a] > deep[b])
	        swap(a, b);
	    int maxn = 0;
	    for (register int i = 16; i >= 0; i--) {
	        if (deep[ance[b][i]] >= deep[a])
	            maxn = max(maxn, mx[b][i]), b = ance[b][i];
	    }
	    if (a == b)
	        return (maxn);
	    for (register int i = 16; i >= 0; i--) {
	        if (ance[a][i] != ance[b][i]) {
	            maxn = max(maxn, max(mx[a][i], mx[b][i]));
	            a = ance[a][i];
	            b = ance[b][i];
	        }
	    }
	    return (max(maxn, max(mx[a][0], mx[b][0])));
	}
	}  // namespace tree
	int ints[100001];
	int find(int n) {
	    if (ints[n] == n)
	        return (n);
	    return (ints[n] = find(ints[n]));
	}
	unsigned char gg[1000001];
	typedef struct _b {
	    int s;
	    int t;
	    int l;
	    friend bool operator<(const _b &a, const _b &b) { return (a.l < b.l); }
	} xiabb;
	xiabb bians[200001];
	double dx;
	typedef struct _n {
	    double k, b;
	    int id;
	    friend bool operator<(const _n &a, const _n &b) { return (a.k * dx + a.b < b.k * dx + b.b); }
	} node;
	int root = 0;
	int ch[1000001][2], fa[1000001];
	node data[1000001];
	int gn = 1;
	inline void xuan(int me) {
	    int tree = fa[me], cjr = fa[tree], op = opp(me), ls = ch[me][op ^ 1];
	    fa[ls] = tree;
	    ch[tree][op] = ls;
	    ch[me][op ^ 1] = tree;
	    if (cjr)
	        ch[cjr][opp(tree)] = me;
	    fa[tree] = me;
	    fa[me] = cjr;
	}
	inline void splay(int tree) {
	    while (fa[tree]) {
	        int cjr = fa[tree];
	        if (fa[cjr])
	            xuan((opp(tree) == opp(cjr)) ? cjr : tree);
	        xuan(tree);
	    }
	}
	void insert_s(int &tree, int me) {
	    if (!tree) {
	        tree = me;
	        return;
	    }
	    insert_s(ch[tree][data[tree] < data[me]], me);
	    fa[ch[tree][data[tree] < data[me]]] = tree;
	}
	inline void insert(node dat) {
	    int me = gn;
	    gn++;
	    data[me] = dat;
	    insert_s(root, me);
	    splay(me);
	    root = me;
	}
	int find(int tree, node dat) {
	    if (dat.k == data[tree].k && dat.b == data[tree].b) {
	        return (tree);
	    }
	    return (find(ch[tree][data[tree] < dat], dat));
	}
	int getmx(int tree) {
	    while (ch[tree][1]) tree = ch[tree][1];
	    return (tree);
	}
	inline void del(node dat) {
	    int me = find(root, dat);
	    splay(me);
	    int ls = ch[me][0], rs = ch[me][1];
	    fa[ls] = 0;
	    fa[rs] = 0;
	    if (!ls) {
	        root = rs;
	        return;
	    }
	    ls = getmx(ls);
	    splay(ls);
	    fa[rs] = ls;
	    ch[ls][1] = rs;
	    root = ls;
	}
	double x[100001], y[100001];
	typedef struct _b_t {
	    int s;
	    int t;
	    int id;
	    friend bool operator<(const _b_t &a, const _b_t &b) {
	        return (atan2(y[a.t] - y[a.s], x[a.t] - x[a.s]) < atan2(y[b.t] - y[b.s], x[b.t] - x[b.s]));
	    }
	} bian_t;
	vector<bian_t> vec[100001];
	int vid[200001];
	int anss[200001];
	typedef struct _pt {
	    double x;
	    double y;
	    unsigned char gj;
	    int id;
	    friend bool operator<(const _pt &a, const _pt &b) {
	        if (a.x != b.x)
	            return (a.x < b.x);
	        return (a.gj > b.gj);
	    }
	} pt;
	pt pts[1000001];
	int val[100001], bel[200001], ss[200001], ts[200001];
	inline double cross(double x1, double y1, double x2, double y2) { return (x1 * y2 - x2 * y1); }
	int getnxt(int tree, double y) {
	    if (!tree)
	        return (0);
	    if (data[tree].k * dx + data[tree].b > y) {
	        int cjr = getnxt(ch[tree][0], y);
	        if (cjr)
	            return (cjr);
	        return (tree);
	    }
	    return (getnxt(ch[tree][1], y));
	}
	void ywymain() {
	    tree::deep[0] = -1;
	    int n = get(), m = get();
	    for (register int i = 1; i <= n; i++) x[i] = get(), y[i] = get(), ints[i] = i;
	    for (register int i = 1; i <= m; i++) {
	        int s = get(), t = get(), l = get();
	        val[i] = l;
	        bian_t cjr;
	        cjr.s = s;
	        cjr.t = t;
	        cjr.id = i;
	        vec[s].push_back(cjr);
	        cjr.s = t;
	        cjr.t = s;
	        cjr.id = i + m;
	        vec[t].push_back(cjr);
	        ss[i] = s;
	        ts[i] = t;
	        ss[i + m] = t;
	        ts[i + m] = s;
	    }
	    for (register int i = 1; i <= n; i++) sort(vec[i].begin(), vec[i].end());
	    for (register int i = 1; i <= n; i++) {
	        for (register int j = 0; j < vec[i].size(); j++) vid[vec[i][j].id] = j;
	    }
	    int gpt = 1;
	    int rt = 0;
	    for (register int i = 1; i <= m * 2; i++) {
	        if (bel[i])
	            continue;
	        int me = gpt;
	        gpt++;
	        double s = 0;
	        int cur = i;
	        do {
	            s += cross(x[ts[cur]] - x[ss[cur]], y[ts[cur]] - y[ss[cur]], x[ts[cur]], y[ts[cur]]);
	            bel[cur] = me;
	            cur = vec[ts[cur]][(vid[(cur > m) ? (cur - m) : (cur + m)] + vec[ts[cur]].size() - 1) %
	                               vec[ts[cur]].size()]
	                      .id;
	        } while (cur != i);
	        if (s >= 0)
	            rt = me;
	    }
	    int ptr = 1;
	    for (register int i = 1; i <= m; i++) {
	        if (bel[i] == rt || bel[i + m] == rt)
	            continue;
	        bians[ptr].s = bel[i];
	        bians[ptr].t = bel[i + m];
	        bians[ptr].l = val[i];
	        ptr++;
	    }
	    sort(bians + 1, bians + ptr);
	    for (register int i = 1; i < ptr; i++) {
	        int aa = find(bians[i].s), ab = find(bians[i].t);
	        if (aa == ab)
	            continue;
	        ints[aa] = ab;
	        tree::add(bians[i].s, bians[i].t, bians[i].l);
	        tree::add(bians[i].t, bians[i].s, bians[i].l);
	    }
	    for (register int i = 1; i < gpt; i++)
	        if (ints[i] == i)
	            tree::dfs(i, 0);
	    for (register int i = 1; i <= 16; i++) {
	        for (register int j = 1; j < gpt; j++) {
	            tree::ance[j][i] = tree::ance[tree::ance[j][i - 1]][i - 1];
	            tree::mx[j][i] = max(tree::mx[j][i - 1], tree::mx[tree::ance[j][i - 1]][i - 1]);
	        }
	    }
	    ptr = 1;
	    for (register int i = 1; i <= n; i++) {
	        pts[ptr].x = x[i];
	        pts[ptr].y = y[i];
	        pts[ptr].id = i;
	        pts[ptr].gj = 1;
	        ptr++;
	    }
	    int q = get();
	    for (register int i = 1; i <= q; i++) {
	        double x1, y1, x2, y2;
	        scanf("%lf%lf%lf%lf", &x1, &y1, &x2, &y2);
	        pts[ptr].x = x1;
	        pts[ptr].y = y1;
	        pts[ptr].gj = 0;
	        pts[ptr].id = i;
	        ptr++;
	        pts[ptr].x = x2;
	        pts[ptr].y = y2;
	        pts[ptr].gj = 0;
	        pts[ptr].id = i + q;
	        ptr++;
	    }
	    sort(pts + 1, pts + ptr);
	    for (register int i = 1; i < ptr;) {
	        int cjr = i;
	        while (cjr < ptr && pts[cjr].x == pts[i].x) cjr++;
	        for (register int j = i; j < cjr; j++) {
	            if (!pts[j].gj)
	                break;
	            for (register int k = 0; k < vec[pts[j].id].size(); k++) {
	                bian_t tmp = vec[pts[j].id][k];
	                if (x[tmp.t] >= x[tmp.s])
	                    continue;
	                dx = pts[i].x - 0.00001;
	                node t;
	                t.k = (y[tmp.t] - y[tmp.s]) / (x[tmp.t] - x[tmp.s]);
	                t.b = y[tmp.t] - x[tmp.t] * t.k;
	                t.id = bel[tmp.id];
	                del(t);
	            }
	        }
	        for (register int j = i; j < cjr; j++) {
	            if (!pts[j].gj)
	                break;
	            for (register int k = 0; k < vec[pts[j].id].size(); k++) {
	                bian_t tmp = vec[pts[j].id][k];
	                if (x[tmp.t] <= x[tmp.s])
	                    continue;
	                dx = pts[i].x + 0.00001;
	                node t;
	                t.k = (y[tmp.s] - y[tmp.t]) / (x[tmp.s] - x[tmp.t]);
	                t.b = y[tmp.s] - x[tmp.s] * t.k;
	                t.id = bel[(tmp.id > m) ? (tmp.id - m) : (tmp.id + m)];
	                insert(t);
	            }
	        }
	        for (register int j = i; j <= cjr; j++) {
	            if (pts[j].gj)
	                continue;
	            dx = pts[j].x + 0.00001;
	            int nx = getnxt(root, pts[j].y);
	            if (!nx) {
	                anss[pts[j].id] = rt;
	                continue;
	            }
	            anss[pts[j].id] = data[nx].id;
	        }
	        i = cjr;
	    }
	    for (register int i = 1; i <= q; i++) {
	        int s = anss[i], t = anss[i + q];
	        if (find(s) != find(t)) {
	            printf("-1\n");
	            continue;
	        }
	        if (s == rt && t == rt) {
	            printf("-1\n");
	            continue;
	        }
	        printf("%d\n", tree::lca(s, t));
	    }
	}
}
int main() {
    ywy::ywymain();
    return (0);
}