自动搬运

查看原文

来自洛谷，原作者为

	冒泡ioa **

搬运于2025-08-24 21:56:11，当前版本为作者最后更新于2018-08-22 20:04:42，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

没思路？我们来找规律！
比如一个$n=5$的排列，我们假设$m=2$也就是说，我们其实已经确定了排列种某些位置的值，就这个例子来说：

$12???$ $1?3??$ $1??4?$ $1???5$ $?23??$ $?2?4?$ $?2??5$ $??34?$ $??3?5$ $???45$

共10种，很容易发现其实就是$C_n^m$，那么其中的问号又多少种排列呢？

没思路？我们再来找规律！
我们设$D_i$为i个?的可能的排列数，显然，$D_1=0$ $D_2=1$
接着我们来看下$D_3$，可以有$312$,$231$
如果我们继续找下去的话，容易出错，所以我们现在来找找规律（灵魂画师）。
就拿$D_4$来说，上面的是数，下面的是位置，首先，1不能放到1号位，而且放到2，3，4上对于递推是等价的，于是他别无选择地放到了其他地方（假设是2号位）

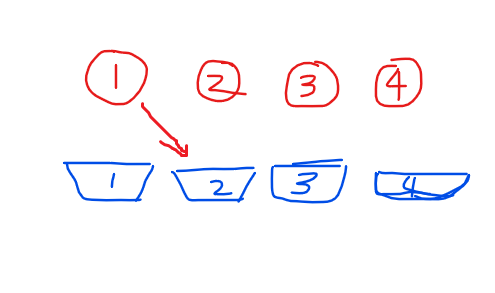
然后我们假设2放到1号位上去，剩下的3，4正好是$D_2$

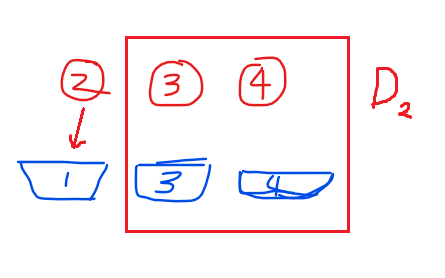
但2怎么可能只有放在1号位上的命运呢？它还可以不放到1号位，咦？我们之前说，i不能放到i号位，那么既然2不放到1号位，那么1号位在这里是不是等价于2号位呢？没错！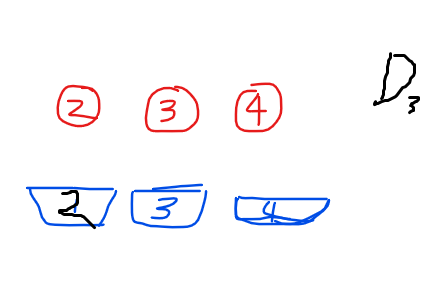
而之前的“万恶之源”数字1，它有$n-1$种放法，所以我们就大胆猜测：$D_n=(n-1)(D_{n-1}+D_{n-2})$
严谨的证明还请大家自己百度
然后我们就愉快地输出$C_n^m\times D_{n-m}$就好啦
其他知识点比如说逆元求组合数（费马小定理）还请大家自行了解

欢迎来我博客玩~

代码

#include<iostream>
#include<cstdio>
using namespace std;
typedef long long ll;
const int MAXN=1000005,mod=1000000007;
ll f[MAXN],inv[MAXN],d[MAXN];
int t;

ll qpow(ll a,ll b){
    ll ans=1;
    while(b){
        if(b&1)ans=a*ans%mod;
        a=a*a%mod;
        b>>=1;
    }
    return ans;
}

void prework(){
    f[0]=1;
    for(int i=1;i<MAXN;i++){
        f[i]=f[i-1]*i%mod;
        inv[i]=qpow(f[i],mod-2);
    }
    d[1]=0,d[2]=1,d[3]=2;
    for(int i=4;i<MAXN;i++){
        d[i]=(i-1)*(d[i-1]+d[i-2])%mod;
    }
}

int main(){
    cin>>t;
    prework();
    for(int i=1;i<=t;i++){
        ll n,m;
        scanf("%lld%lld",&n,&m);
        if (n - m == 1) printf("0\n");
        else if (m == n) printf("1\n");
        else if (m == 0) printf("%lld\n",d[n]);
        else {
            printf("%lld\n",f[n] * inv[m] % mod * inv[n-m] % mod * d[n-m] % mod);
        }
    }
    return 0;
}