自动搬运

查看原文

来自洛谷，原作者为

	zxtikes **

搬运于2025-08-24 21:55:53，当前版本为作者最后更新于2022-05-17 19:57:37，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

前言

当一个蒟蒻开始了今天的做题，欣喜地开启了一道题。经过几番思索之后，果断地开始写起了 模拟退火。

很显然，如果我们考虑动态规划，会发现状态很多，难以储存；如果我们考虑搜索，枚举每一个可能的序列，再计算出最大得分，复杂度是 $O(n!)$，很明显的 TLE 瞬间起飞。接下来思考其他的做法，都是一筹莫展。

最后还是选择我们的 模拟退火，模拟退火骗分就是好。

说明

接下来讲解一下模拟退火大概是什么东西。

模拟退火适用于具有连续性的函数，具体地讲，是适用于，将一个问题的解决方式进行细微改变，所得到的答案改变也不会非常大的问题。

模拟退火不一定能得到真正的最优解，但是可以得到一个函数的 局部最优解，所以我们进行模拟退火一般进行多次，从而得到多个局部最优解，这样子，我们得到全局最优解的概率就大大提升。

模拟退火所求函数一般不规则，但是具有一定连续性。

例如如下函数：

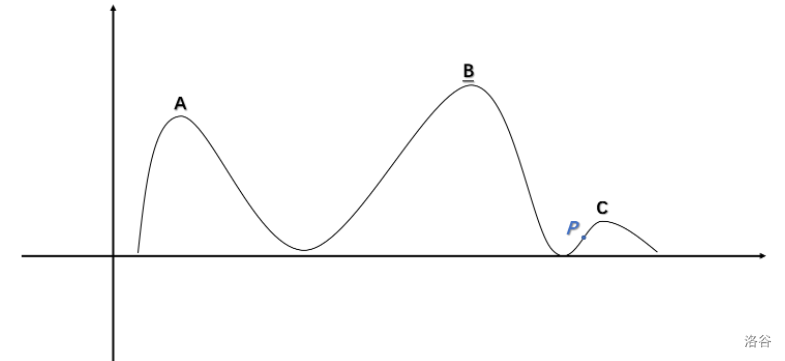
其中 $A, B, C$ 都是一个局部最优解，但我们观察到，$B$ 才是全局最优解，但是我们一次退火很难保证就很求到 $B$ 这个答案，所以要多次退火，才会有更大的概率得到全局最优解。

通常，模拟退火有如下几个概念：

1. 初始温度 $T_0$，表示最开始随机的范围大小。

2. 终止温度 $T_E$，表示我们这次退火结束的温度。一般情况下 $T_E \rightarrow 0$ 。

3. 衰减系数 $T_x$， $0<T_x<1$ 表示每一次退火温度的衰减值。一般情况下 $T_x>0.9$ ，这样子才能保证所得到的答案足够精确，如果 $T_x<0.9$ ，那么所得到的答案就很难保证是最优解了，虽然退火本身就玄学。

4. 概率 $P$ ，表示我们从一个候补答案，更新为另一个候补答案的概率。其中，如果我们的新候补答案大于当前答案，那么概率 $P=1$ 也就是一定会更新答案；否则，我们将以一定的概率来决定是否更新。一般情况下，这个概率为：$P=e^{-\Delta/t}$ （题目要求求最大值），或者，$P=e^{\Delta/t}$ （题目要求求最小值） ，其中 $\Delta=new-now$， $new$ 表示新候补答案，$now$ 表示当前答案，$t$ 一般情况下会用来表示答案变化范围，普遍性取值为温度 $T$ ，这样保证 $0<P<1$ ，并且 $P$ 随着 $\Delta$ 的改变而改变，具体改变是正相关还是负相关，与题目求是最大值还是最小值有关。

以上 $T_x$ 主要决定了模拟退火的复杂度，$T_x$ 越大，复杂度越低，所得到的答案的精确度越高。

经过个人测试，此题需要要求 $T_x>0.94$， 别问我怎么测出来的。

题目分析

在本题中，对于每个轮次，有三种情况：全中，补中，失误。我们需要将打出的所有轮次的顺序重新排列，使得得分最高。

其中，补中会使选手在下一轮中的第一次尝试的得分将会以双倍计入总分。失误的情况属于一般情况，不具有特殊性，所以不做处理。最重要的是全中的情况。全中会使选手在计算总分时，下一轮的得分将会被乘 $2$ 计入总分，最需要 特殊处理 的是，当原来最后一轮次全中，我们在重新排列的时候，也需要最后一轮次是全中，因为这样子才会有奖励的轮次，需要进行的轮数和重排前所进行的轮数是一致的，才满足题意。

本题目中，我们用温度 $T$ ，表示答案更新范围，当 $T \rightarrow 0$，也就是达到终止温度 $T_E$ 时，我们就获得了一个候补答案。

最后我们进行多次退火就可以了。

什么？你说你不知道该进行多少次退火？不会计算复杂度？

这里有一个很方便的函数，可以帮助你卡着时间过，让你放心且愉悦。

while ((double)clock()/CLOCKS_PER_SEC<0.8)

$\text{clock}$ 是一个表示时间单位的函数，具体怎么表示，我也不清楚，每个编译器版本不同，这个函数表示的时间单位一般不同。但是我们有一个表示单位时间为 $1s$ 的常量 $\text{CLOCKS\_PER\_SEC}$，我们用 $\text{clock}$ 相除就可以换算成以秒作为单位的数了。在题目时间限制为 $1s$ 时，一般我们循环条件是小于 $0.8$ ，因为如果是 $0.9$ 以上，或者直接为 $1$ ，是可能会超时的，因为最后一次模拟退火万一时间复杂度突然高起来，就会造成这种情况，所以为了保险，一般就是 $0.8$ 。

如果你不喜欢用卡时，那么这个退火的次数一般进行 $1000 \sim 5000$ 次。

一般 $T_x$ 越大 ，这个次数可以适当低，但最好让次数多一些。

经过测试，当 $T_x=0.95$ 时，次数需要等于2000，只有90分，3000就可以成功 AC 。别问我怎么知道的。

所以还是卡时安心一些。

对于每次的新的答案，我们用函数 $\text{calc}$ 求出，求得方式与题意相同。

代码展示

说了很多话，大家看的其实还是很抽象的，所以还是放代码，帮助大家理解一下实现的思路。

#include<bits/stdc++.h>
#define ll long long
#define inf 1e9
#define rep(i,l,r) for(register int i=l;i<=r;++i)
#define per(i,r,l) for(register int i=r;i>=l;--i)
#define x first
#define y second
using namespace std;
const int N=55;
typedef pair<int,int> pii;

int n,m;
pii q[N];//pair 存储每一个轮次 
int ans;
inline int calc(){//计算函数 
	int ret=0;
	rep(i,1,m){
		ret+=q[i].x+q[i].y;
		if(i<=n){
			if(q[i].x==10)ret+=q[i+1].x+q[i+1].y;//全中情况 
			else if(q[i].x+q[i].y==10)ret+=q[i+1].x;// 补中情况 
		}
	}
	ans=max(ans,ret);// 更新答案 
	return ret;
}
inline void simulate_anneal(){//模拟退火函数 
	
	// 初始温度T0 1e4 终止温度Te 1e-4 衰减系数Tx 0.97 
	for(double t=1e4;t>1e-4;t*=0.97){
		int a=rand()%m+1,b=rand()%m+1;
		int now=calc();
		swap(q[a],q[b]);//得到下一个随机的情况 
		if(n+(q[n].x==10)==m){
			int nxt=calc();//得到下一个答案的情况 
			int delta=nxt-now;//求答案改变量delta 
			if(exp(delta/t)<(double)rand()/RAND_MAX)swap(q[a],q[b]);//以一定的概率是否更新答案 
		}
		else swap(q[a],q[b]);
	}
}
int main(){
	scanf("%d",&n);
	rep(i,1,n)scanf("%d%d",&q[i].x,&q[i].y);
	if(q[n].x==10)m=n+1,scanf("%d%d",&q[m].x,&q[m].y);//处理最后一轮次情况 
	else m=n;
	while ((double)clock()/CLOCKS_PER_SEC<0.8)simulate_anneal();//卡时  模拟退火 
	printf("%d\n",ans);//输出答案 
	return 0;
}