1 条题解
-
0
自动搬运
来自洛谷,原作者为

Iowa_BattleShip
AFO/kel搬运于
2025-08-24 21:55:34,当前版本为作者最后更新于2018-04-03 20:15:16,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
很明显,这题是道最大费用最大流,只不过强行加上规则来导致你的码量轻松上天。
下面将三个规则一个一个解释如何建图
规则一
其实我认为三个规则里第一个反而是相对最难的条路径皆不能相交,即点和边都不能相交。
首先,要使得路径上的点不相交(重合),即每个点只能走一次,因此我们想到将每个点拆成两个点和,并在和之间连一条容量为,费用为该点本身的数值的边,当选中这条边就表示某条路径经过点,并将该点数值计入。
接下来是连边,其实很简单,将点向和连上一条边,而根据下图,显然我们可以看出当点不相交时,边肯定是不会相交的,所以我们在添加边的时候容量是可以随便开的(当然要),费用则赋为。
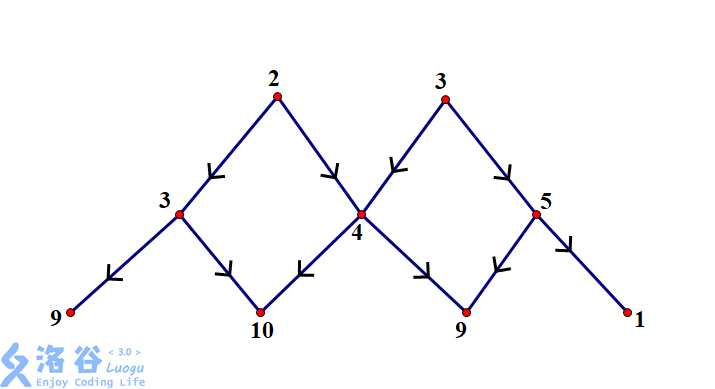
最后按照惯例,给图加上一个超级源点和超级汇点,向每个连一条容量为,费用为的边;每个向连一条容量为,费用为的边。
然后跑一波最大费用最大流即可。
规则二
这下只要求边不相交(重合)了,所以可以不用拆点了。
直接连边,给每个点向和连上一条边,容量为(因为每条边只能走一次,而根据上图,边只会重合),费用则赋为点所表示的数值,即经过这条边表示选取了这个点的数(其实规则一中也可以这样连边,然后将拆点间的边的容量改为即可)。
最后依旧定个超级源点和超级汇点,依旧向每个连一条容量为,费用为的边;而每个向连一条容量为的边(因为每个都可以取次),费用为所表示的数值。
然后依旧一波最大费用最大流。
规则三
其实就是没有规则只需将规则二所连的边,除了与连的边,其他边的容量全部改为就好,因为所有点和边都可以重复走了。
然后一波最大费用最大流带走~
关于规则三我认为完全可以用跑过去,将这个梯形拆成个三角形,然后直接,复杂度大概为,是可以跑过去的。
最后上
冗长的代码#include<cstdio>//我用的是带SPFA的EK #include<cstring> using namespace std; const int N=1e5+10; int fi[N],di[N<<1],da[N<<1],ne[N<<1],co[N<<1],q[N],la[N],nm[N],dis[N],a[22][50],b[22][50],l,st=1e5+1,ed=1e5+2,s; //fi,di,da,ne,co存边,q为队列,la,nm记录在SPFA中搜到的分层图,dis记录费用,a为原图,b为原图中每个数对应的编号,st是源点,ed是汇点 bool v[N];//在SPFA中记录该点有无在队列中 int re()//快读 { int x=0; char c=getchar(); bool p=0; for(;c<'0'||c>'9';c=getchar()) p=(c=='-'||p)?1:0; for(;c>='0'&&c<='9';c=getchar()) x=x*10+(c-'0'); return p?-x:x; } void add(int x,int y,int z,int c)//加边 { di[++l]=y; da[l]=z; co[l]=c; ne[l]=fi[x]; fi[x]=l; di[++l]=x; da[l]=0; co[l]=-c; ne[l]=fi[y]; fi[y]=l; } inline int minn(int x,int y)//手写min { return x<y?x:y; } void cl()//每次跑完后重建图前的清空 { l=s=0; memset(fi,0,sizeof(fi)); memset(di,0,sizeof(di)); memset(da,0,sizeof(da)); memset(ne,0,sizeof(ne)); memset(co,0,sizeof(co)); } bool spfa()//SPFA { int head=0,tail=1,x,y,i; memset(dis,-50,sizeof(dis));//初始化为-inf memset(v,0,sizeof(v)); q[1]=st; dis[st]=0; while(head!=tail) { head++; x=q[head]; v[x]=0; for(i=fi[x];i;i=ne[i])//枚举边 { y=di[i]; if(da[i]>0&&dis[y]<dis[x]+co[i])//找到最大费用 { dis[y]=dis[x]+co[i]; la[y]=x;//记录分层图 nm[y]=i; if(!v[y])//若不在队列则加入队列 { tail++; q[tail]=y; v[y]=1; } } } } return dis[ed]>0;//判断ed有无走到 } void ek()//EK { int i,mi; while(spfa()) { mi=1e9; for(i=ed;i!=st;i=la[i])//从分层图的ed枚举到st,找到最小的流量 mi=minn(mi,da[nm[i]]); s+=mi*dis[ed];//累计每次的费用 for(i=ed;i!=st;i=la[i])//修改容量 { da[nm[i]]-=mi; da[((nm[i]+1)^1)-1]+=mi; } } } int main() { int i,j,n,m,k,o,nu=0; k=m=re(); n=re(); o=(((m*n)<<1)+n*n-n)>>1;//等差数列求和公式+梯形面积公式,算出一共有多少数,拆点时区分编号用 for(i=1;i<=n;i++,k++) for(j=1;j<=k;j++) { a[i][j]=re(); b[i][j]=++nu;//输入的同时给点赋上编号 } k=m; for(i=1;i<=k;i++) add(st,b[1][i],1,0);//连上源点 for(i=1;i<n;i++,k++) for(j=1;j<=k;j++) { add(b[i][j],b[i][j]+o,1,a[i][j]);//给拆点间连边 add(b[i][j]+o,b[i+1][j],1,0);//向左下和右下连边 add(b[i][j]+o,b[i+1][j+1],1,0); } for(i=1;i<=k;i++) { add(b[n][i],b[n][i]+o,1,a[n][i]);//拆点间连边 add(b[n][i]+o,ed,1,0);//向汇点连边 } ek();//跑最大费用最大流 printf("%d\n",s); cl();//清空重建 k=m; for(i=1;i<=k;i++) add(st,b[1][i],1,0);//连源点 for(i=1;i<n;i++,k++) for(j=1;j<=k;j++) { add(b[i][j],b[i+1][j],1,a[i][j]);//不需要拆点了,直接向左下右下连边 add(b[i][j],b[i+1][j+1],1,a[i][j]); } for(i=1;i<=k;i++) add(b[n][i],ed,1e9,a[n][i]);//向汇点连边,容量为inf ek();//再来跑一遍 printf("%d\n",s); cl();//同样清空 k=m; for(i=1;i<=k;i++) add(st,b[1][i],1,0);//连汇点 for(i=1;i<n;i++,k++) for(j=1;j<=k;j++) { add(b[i][j],b[i+1][j],1e9,a[i][j]);//向左下右下连边,容量为inf add(b[i][j],b[i+1][j+1],1e9,a[i][j]); } for(i=1;i<=k;i++) add(b[n][i],ed,1e9,a[n][i]);//向汇点连边,容量为inf ek();//最后一波带走~ printf("%d\n",s); return 0; }
- 1
信息
- ID
- 2967
- 时间
- 1000ms
- 内存
- 250MiB
- 难度
- 6
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
