自动搬运

查看原文

来自洛谷，原作者为

	liangbowen 不能再摆了，，，

搬运于2025-08-24 21:55:33，当前版本为作者最后更新于2023-01-18 09:16:38，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

前言

题目传送门！

更好的阅读体验？

网络流 $24$ 题：最大费用最大流。还算简单且套路的一道题。

快捷步骤

这里先说两点。第一点，很多题解提到了，输入非常麻烦，需要类似于把图翻过来的操作。

这实际上是完全没必要的。你把全部点翻了和没翻一样，为啥要翻。而且翻了也不会让你理解起来更顺畅。

第二点，实际上，没必要费心思给每一个点编号。你直接用 idx 记录下全部点即可。

这也是非常显然的事情。

s = ++idx, t = ++idx;
for (int i = 0; i <= n; i++)
    for (int j = 0; j <= m; j++)
        id[i][j] = ++idx; //给每个点一个编号

思路

首先我们只看每一个点。是典型的方格取数问题，可以考虑费用流。

对于一个相邻的、可以走到的点 $(x, y)$ 与 $(dx, dy)$，我们可以直接连边 $(x,y) \xrightarrow{cap=1\ cost=w} (dx,dy)$，表示：你想拿到这个格子的价值，那么你只能拿一次。

但是这样并不对。因为只是这样子，代表这一条边只能走一次。很显然这是不对的，因为你可以走这条边，但是什么都不拿。

于是我们再建一条 $(x,y) \xrightarrow{cap=\infty \ cost=0} (dx,dy)$，表示：这条边随便走，但是没有费用。

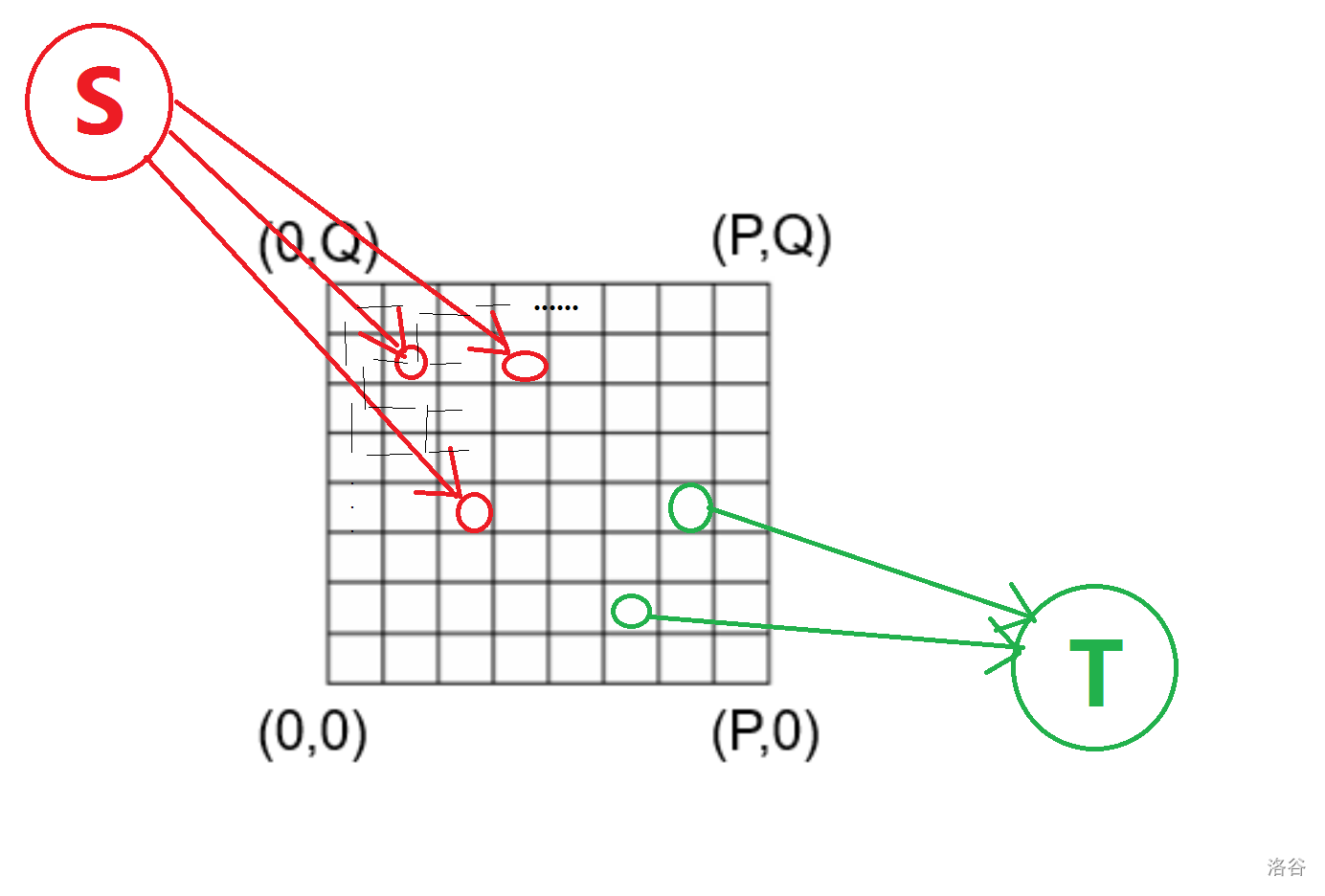
这就是第一步。我们再看一下源点与汇点：那 $a$ 个点就是源点，那 $b$ 个点就是汇点。

很套路地，建立多源多汇即可：超级源点连向每一个源点，超级汇点连向每一个汇点。

具体地：

• 假设有 $k$ 个深海机器人从 $(x, y)$ 位置出发，就 $S \xrightarrow{cap=k \ cost=0} (x, y)$。
• 假设有 $r$ 个深海机器人从 $(x, y)$ 位置作为目的地，就 $(x,y) \xrightarrow{cap=k \ cost=0} T$。

于是这题就做完了。您也可以尝试看看下面这张图：

代码

最多的点数应该是 $nm$ 的级别（还要多一些），可以直接按 $400$ 算。

最多的边数大概是 $2 \times (2nm + 2nm + a + b) = 8nm+2a+2b \approx 8\times400+2\times10+2\times10=3240$（反正开多一点准没错）。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
using namespace std;
/**********最大费用最大流模版，可以自己写**********/
const int N = 400, inf = 0x3f3f3f3f;
struct Edge {int now, nxt, w, cost;} e[3240];
int head[N], cur = 1;
void ad(int u, int v, int  w, int cost)
{
    e[++cur].now = v, e[cur].nxt = head[u], e[cur].w = w, e[cur].cost = cost;
    head[u] = cur;
}
void add(int u, int v, int w, int cost) {ad(u, v, w, cost), ad(v, u, 0, -cost);}
int dis[N], icost[N], pre[N]; bool inque[N];
int s, t;
bool spfa()
{
    queue <int> q;
    memset(dis, -0x3f, sizeof dis), memset(icost, 0, sizeof icost);
    q.push(s), dis[s] = 0, icost[s] = inf, inque[s] = true;
    while (!q.empty())
    {
        int u = q.front();
        q.pop(), inque[u] = false;
        for (int i = head[u]; i; i = e[i].nxt)
        {
            int v = e[i].now;
            if (!e[i].w) continue;
            if (dis[u] + e[i].cost > dis[v])
            {
                dis[v] = dis[u] + e[i].cost, pre[v] = i;
                icost[v] = min(icost[u], e[i].w);
                if (!inque[v]) q.push(v), inque[v] = true;
            }
        }
    }
    return icost[t] > 0;
}
int EK()
{
    int ans = 0;
    while (spfa())
    {
        int w = icost[t];
        ans += w * dis[t];
        for (int i = t; i != s; i = e[pre[i] ^ 1].now)
            e[pre[i]].w -= w, e[pre[i] ^ 1].w += w;
    }
    return ans;
}
/**********最大费用最大流模版，可以自己写**********/
int id[20][20];
int main()
{
    int a, b, n, m, idx = 0;
    scanf("%d%d%d%d", &a, &b, &n, &m);
    s = ++idx, t = ++idx;
    for (int i = 0; i <= n; i++)
        for (int j = 0; j <= m; j++)
            id[i][j] = ++idx; //给每个点编号
    for (int i = 0; i <= n; i++)
        for (int j = 0; j < m; j++)
        {
            int w;
            scanf("%d", &w);
            add(id[i][j], id[i][j + 1], 1, w), add(id[i][j], id[i][j + 1], inf, 0); //建立相邻点的边
        }
    for (int j = 0; j <= m; j++)
        for (int i = 0; i < n; i++)
        {
            int w;
            scanf("%d", &w);
            add(id[i][j], id[i + 1][j], 1, w), add(id[i][j], id[i + 1][j], inf, 0); //建立相邻点的边
        }
    while (a--) //建立超级源点与多个源点的边
    {
        int w, i, j;
        scanf("%d%d%d", &w, &i, &j);
        add(s, id[i][j], w, 0);
    }
    while (b--) //建立超级汇点与多个汇点的边
    {
        int w, i, j;
        scanf("%d%d%d", &w, &i, &j);
        add(id[i][j], t, w, 0);
    }
    cout << EK();
    return 0;
}

希望能帮助到大家！