自动搬运

查看原文

来自洛谷，原作者为

	钱逸凡 **

搬运于2025-08-24 21:55:27，当前版本为作者最后更新于2018-08-12 15:59:59，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

打了几个小时终于A了（我真是太蒻了），第一次A黑题，兴奋地发了个题解

推荐一波我的博客

很好的网络流题

本题是费用流。（根本看不出来）

首先要知道怎么判断图是否漏水。

方法如下：

考虑黑白染色法：

把网格染成黑白相间的格子，把每一个白色当成源点，每一个黑色当成汇点。

把每个格子周围建立四个点，白色（源点）连向能通的周围点，黑色周围点连向汇点。

把白色的周围点连向黑色周围点。

什么意思呢？

以下图为例：

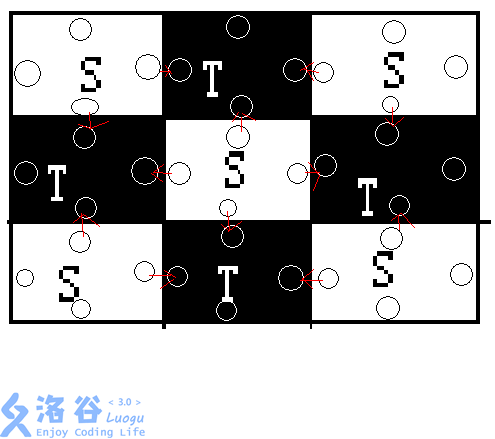
对于一张不会漏的图，如：（画图技术有限）

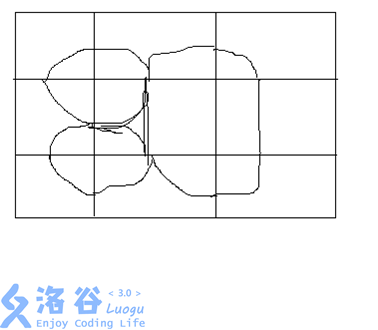
我们连以下边：

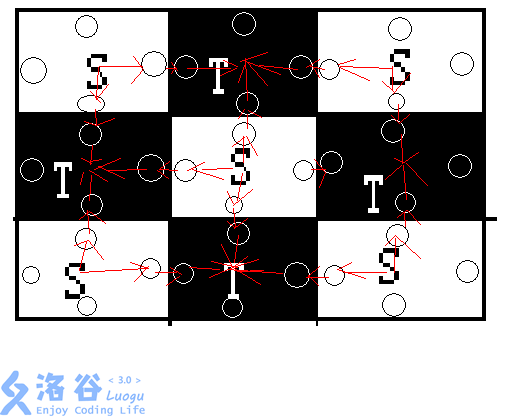
这时，满流就等价于不会漏。

接下来考虑旋转的问题：

先找一张会漏但经过旋转就不会漏的图：

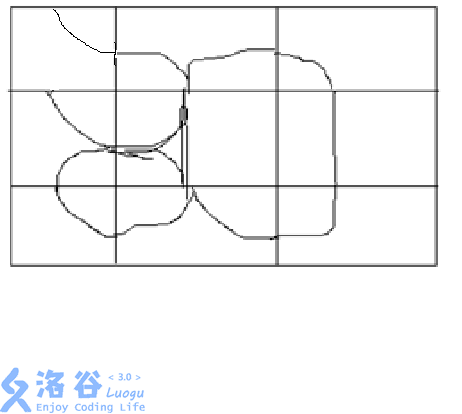
将左上角旋转一次就不会漏。

那转化回黑白图是什么呢？

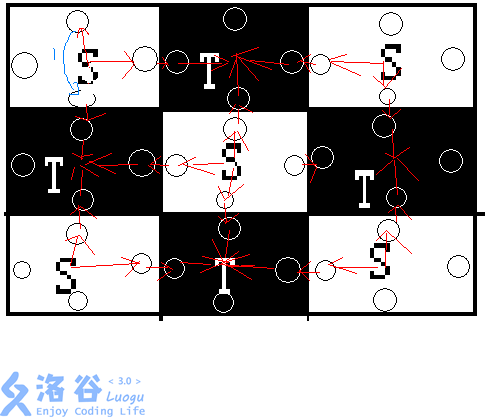为了满足旋转，我们加入一条蓝色的边，代价为1。

然后我们跑费用流，红色的流量为1，代价为0，蓝色的流量为1，代价为1，答案即是1，也就是需要旋转的次数。

讲到这里，大概你就懂了。

没错，只要把每个格子对应的红边蓝边加好，跑费用流即可。

题目里给的水管可以分为5类：

以下全部默认白格，黑格所有边反向

1.直线型：

：

由于不用旋转，只需把对应的红边加好，既s指向上和s指向下。

2.Q型：

对于这种，我们需要加入一条红边，从s（源点）指向初始方向（以向上为例），加入蓝边，上指向左，代价为1，上指向右，代价为1，上指向下，代价为2（要旋转两次）。

3.丁型：

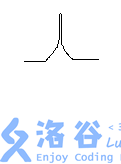
我们需要加入三条红边：s指向上，s指向左，s指向右， 还有三条蓝边：上指向下，代价为2（旋转两次），左指向下，代价为1（旋转一次），右指向下，代价为1（旋转一次）。//这个地方旋转要自己画图理解

4.L型：

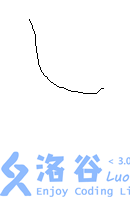
我们需要加入两条红边：s指向上，s指向右，再加入两条蓝边：上指向下,代价为1，（旋转一次，因为旋转一次后，仍有指向右的，故只需改上的）右指向左，代价为1。

是不是很奇怪，没有代价为2的边，其实旋转两次相当于两条蓝边都走，总代价就是2了。

5.+型：

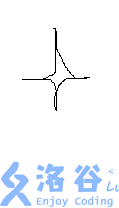
由于这种不能旋转，直接加4条红边即可。

这题的难点在于建图，图建好了跑费用流就能过了。

附上我丑陋的代码： 打了三百多行累死我了，不过其实很多情况可以合并的。

#include<iostream>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
using namespace std;
const int inf=1<<30;
int Read(){
    int x=0,f=1;
    char c=getchar();
    while(c>'9'||c<'0'){
        if(c=='-')f=-1;
    c=getchar();    
    }
    while(c>='0'&&c<='9')x=x*10+c-'0',c=getchar();
    return f==1?x:-x;
}
int maxflow=0;
int mincost=0;
int realflow=0;
int n,m;
int top=1,head[101010],inque[101010];
int s,t;
int dist[101010];
struct Node{
    int v;
    int val;
    int next;
    int cost;
}node[101010];
void addedge(int u,int v,int val,int cost){
    node[++top].v=v;
    node[top].val=val;
    node[top].cost=cost;
    node[top].next=head[u];
    head[u]=top;
}//加边函数 
void add(int u,int v,int val,int cost){
    addedge(u,v,val,cost);
    addedge(v,u,0,-cost);
}//网络流的加边，正向和反向 
bool spfa(){
    memset(inque,0,sizeof(inque));
    memset(dist,0x3f,sizeof(dist));
    dist[s]=0;
    inque[s]=1;
    queue<int>q;
    q.push(s);
    while(!q.empty()){
        int u=q.front();
        q.pop();
        inque[u]=0;
        for(int i=head[u];i;i=node[i].next){
            int d=node[i].v;
            if(dist[d]>dist[u]+node[i].cost&&node[i].val){
                dist[d]=dist[u]+node[i].cost;
                if(inque[d]==0){
                    q.push(d);
                    inque[d]=1;
                }
            }
        }
    }
    return dist[t]!=0x3f3f3f3f;
}
inline int min(int x,int y){
    return x<y?x:y;
}
int dfs(int u,int low){
    if(u==t){inque[t]=1;maxflow+=low;return low;}
    int used=0;
    inque[u]=1;
    for(int i=head[u];i;i=node[i].next){
        int d=node[i].v;
        if((inque[d]==0||d==t)&&node[i].val!=0&&dist[d]==dist[u]+node[i].cost){
            int minflow=dfs(d,min(low-used,node[i].val));
            if(minflow!=0)
            mincost+=node[i].cost*minflow,node[i].val-=minflow,node[i^1].val+=minflow,used+=minflow;
            
            if(used==low)break;
        }
    }
    return used;
}
int Dinic(){
    while(spfa()){
        inque[t]=1;
        while(inque[t]){
        memset(inque,0,sizeof(inque));
        dfs(s,inf);
        } 
    }
    return maxflow;
}
inline bool check(int i,int j){
    return i>0&&i<=n&&j>0&&j<=m;
}//判断(i,j)是否需要加节点 
inline int up(int i,int j){
    return 4*((i-1)*m+j);
}//(i,j)的上节点 
inline int down(int i,int j){
    return 4*((i-1)*m+j)+1;
}//(i,j)的下节点 
inline int left(int i,int j){
    return 4*((i-1)*m+j)+2;
}//(i,j)的左节点 
inline int right(int i,int j){
    return 4*((i-1)*m+j)+3;
}//(i,j)的右节点 
int main() {
    //freopen("cin.txt","r",stdin);
    s=10010,t=10001;
    n=Read(),m=Read();
    int i,j;
    int map,colur;
    colur=0;
    for(i=1;i<=n;i++){
    	colur=i%2;
        for(j=1;j<=m;j++){
            map=Read();
            colur^=1;
            if(colur==0){
            if(check(i,j-1))add(left(i,j),right(i,j-1),1,0);
            if(check(i,j+1))add(right(i,j),left(i,j+1),1,0);
            if(check(i-1,j))add(up(i,j),down(i-1,j),1,0);
            if(check(i+1,j))add(down(i,j),up(i+1,j),1,0);
            }//白色点四周与附近的黑色点四周相连
            if(map==1){//0001
            realflow++;
            if(colur==0){
            add(s,up(i,j),1,0);
            add(up(i,j),right(i,j),1,1);//向右流要转一次，代价为1
            add(up(i,j),left(i,j),1,1);//向左代价为1
            add(up(i,j),down(i,j),1,2);//向下代价为2 
            }//白色点s向四周流 
            if(colur==1){
            add(up(i,j),t,1,0);
            add(right(i,j),up(i,j),1,1);
            add(left(i,j),up(i,j),1,1);
            add(down(i,j),up(i,j),1,2);
            }//黑色点四周向t流 
            continue;
            }
            if(map==2){//0010
            realflow++;
            if(colur==0){
            add(s,right(i,j),1,0);
            add(right(i,j),up(i,j),1,1);
            add(right(i,j),down(i,j),1,1);
            add(right(i,j),left(i,j),1,2);
            }
            if(colur==1){
            add(right(i,j),t,1,0);
            add(up(i,j),right(i,j),1,1);
            add(down(i,j),right(i,j),1,1);
            add(left(i,j),right(i,j),1,2);
            }
            continue;
            }
            if(map==3){//0011
            realflow+=2;
            if(colur==0){
            add(s,up(i,j),1,0);
            add(s,right(i,j),1,0);
            add(up(i,j),down(i,j),1,1);
            add(right(i,j),left(i,j),1,1);
            }
            if(colur==1){
            add(up(i,j),t,1,0);
            add(right(i,j),t,1,0);
            add(down(i,j),up(i,j),1,1);
            add(left(i,j),right(i,j),1,1);
            }
            continue;
            }
            if(map==4){//0100
            realflow++;	
            if(colur==0){
            add(s,down(i,j),1,0);
            add(down(i,j),right(i,j),1,1);
            add(down(i,j),left(i,j),1,1);
            add(down(i,j),up(i,j),1,2);
            }
            if(colur==1){
            add(down(i,j),t,1,0);
            add(right(i,j),down(i,j),1,1);
            add(left(i,j),down(i,j),1,1);
            add(up(i,j),down(i,j),1,2);
            }
            continue;
            }
            if(map==5){//0101
            realflow+=2;
            if(colur==0){
            add(s,up(i,j),1,0);
            add(s,down(i,j),1,0);
            }
            if(colur==1){
            add(up(i,j),t,1,0);
            add(down(i,j),t,1,0);
            }
            }//直线型不可旋转
            if(map==6){//0110
            realflow+=2;
            if(colur==0){
            add(s,right(i,j),1,0);
            add(s,down(i,j),1,0);
            add(right(i,j),left(i,j),1,1);
            add(down(i,j),up(i,j),1,1);
            }
            if(colur==1){
            add(right(i,j),t,1,0);
            add(down(i,j),t,1,0);
            add(left(i,j),right(i,j),1,1);
            add(up(i,j),down(i,j),1,1);
            }
            } 
            if(map==7){//0111
            realflow+=3;
            if(colur==0){
            add(s,up(i,j),1,0);
            add(s,right(i,j),1,0);
            add(s,down(i,j),1,0);
            add(up(i,j),left(i,j),1,1);
            add(down(i,j),left(i,j),1,1);
            add(right(i,j),left(i,j),1,2);
            }
            if(colur==1){
            add(up(i,j),t,1,0);
            add(right(i,j),t,1,0);
            add(down(i,j),t,1,0);
            add(left(i,j),up(i,j),1,1);
            add(left(i,j),down(i,j),1,1);
            add(left(i,j),right(i,j),1,2);
            }
            }
            if(map==8){//1000
            realflow++;
            if(colur==0){
            add(s,left(i,j),1,0);
            add(left(i,j),up(i,j),1,1);
            add(left(i,j),down(i,j),1,1);
            add(left(i,j),right(i,j),1,2);
            }
            if(colur==1){
            add(left(i,j),t,1,0);
            add(up(i,j),left(i,j),1,1);
            add(down(i,j),left(i,j),1,1);
            add(right(i,j),left(i,j),1,2);
            }
            }
            if(map==9){//1001
            realflow+=2;
            if(colur==0){
            add(s,up(i,j),1,0);
            add(s,left(i,j),1,0);
            add(up(i,j),down(i,j),1,1);
            add(left(i,j),right(i,j),1,1);
            }
            if(colur==1){
            add(up(i,j),t,1,0);
            add(left(i,j),t,1,0);
            add(down(i,j),up(i,j),1,1);
            add(right(i,j),left(i,j),1,1);
            }
            }
            if(map==10){//1010
            realflow+=2;
            if(colur==0){
            add(s,left(i,j),1,0);
            add(s,right(i,j),1,0);
            }
            if(colur==1){
            add(left(i,j),t,1,0);
            add(right(i,j),t,1,0);
            }
            continue;//直线型 
            }
            if(map==11){//1011
            realflow+=3;
            if(colur==0){
            add(s,up(i,j),1,0);
            add(s,left(i,j),1,0);
            add(s,right(i,j),1,0);
            add(left(i,j),down(i,j),1,1);
            add(right(i,j),down(i,j),1,1);
            add(up(i,j),down(i,j),1,2);
            }
            if(colur==1){
            add(up(i,j),t,1,0);
            add(left(i,j),t,1,0);
            add(right(i,j),t,1,0);
            add(down(i,j),left(i,j),1,1);
            add(down(i,j),right(i,j),1,1);
            add(down(i,j),up(i,j),1,2);
            }
            }
            if(map==12){//1100
            realflow+=2;
            if(colur==0){
            add(s,left(i,j),1,0);
            add(s,down(i,j),1,0);
            add(left(i,j),right(i,j),1,1);
            add(down(i,j),up(i,j),1,1);
            }
            if(colur==1){
            add(left(i,j),t,1,0);
            add(down(i,j),t,1,0);
            add(right(i,j),left(i,j),1,1);
            add(up(i,j),down(i,j),1,1);
            }
            }
            if(map==13){//1101
            realflow+=3;
            if(colur==0){
            add(s,up(i,j),1,0);
            add(s,down(i,j),1,0);
            add(s,left(i,j),1,0);
            add(up(i,j),right(i,j),1,1);
            add(down(i,j),right(i,j),1,1);
            add(left(i,j),right(i,j),1,2);
            }
            if(colur==1){
            add(up(i,j),t,1,0);
            add(down(i,j),t,1,0);
            add(left(i,j),t,1,0);
            add(right(i,j),up(i,j),1,1);
            add(right(i,j),down(i,j),1,1);
            add(right(i,j),left(i,j),1,2);
            }
            }
            if(map==14){//1110
            realflow+=3;
            if(colur==0){
            add(s,left(i,j),1,0);
            add(s,down(i,j),1,0);
            add(s,right(i,j),1,0);
            add(left(i,j),up(i,j),1,1);
            add(right(i,j),up(i,j),1,1);
            add(down(i,j),up(i,j),1,2);
            }	
            if(colur==1){
            add(left(i,j),t,1,0);
            add(down(i,j),t,1,0);
            add(right(i,j),t,1,0);
            add(up(i,j),left(i,j),1,1);
            add(up(i,j),right(i,j),1,1);
            add(up(i,j),down(i,j),1,2);	
            }
            }
            if(map==15){//1111
            realflow+=4;
            if(colur==0){
            add(s,up(i,j),1,0);
            add(s,right(i,j),1,0);
            add(s,left(i,j),1,0);
            add(s,down(i,j),1,0);	
            }
            if(colur==1){
            add(up(i,j),t,1,0);
            add(down(i,j),t,1,0);
            add(left(i,j),t,1,0);
            add(right(i,j),t,1,0);
            }
            }
        }
    }
    Dinic();
    if(maxflow*2!=realflow)printf("-1");
    else printf("%d",mincost);
    return 0;
}

需要注意的是，无论黑白，在统计应该的流量（代码中为realflow）时一视同仁，最后只需最大流等于应该的流量即为满流。

看懂了就给个赞吧。

没看懂可以发讨论。