自动搬运

查看原文

来自洛谷，原作者为

	revenger **

搬运于2025-08-24 21:55:06，当前版本为作者最后更新于2018-04-26 18:34:31，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

看到这道题，我们先来画一下柿子。

$D=(A*B-C)*A^T$

$D=\sum_{i=1}^n(\sum_{j=1}^na_j*b_{j,i}-c_i)*a_i$

$D=\sum_{i=1}^n\sum_{j=1}^na_i*a_j*b_{i,j}-\sum_{i=1}^na_i*c_i$

柿子画到这里，我们可以看出，对于每个$a_i$，选0的时候没有贡献，选1的时候会带来$c_i$的损失，但是对于每一个同样选1的$a_j$,会带来$b_{j,i}+b_{i,j}$的贡献。

结合数据范围$n\leq500$,可以联想到最小割。

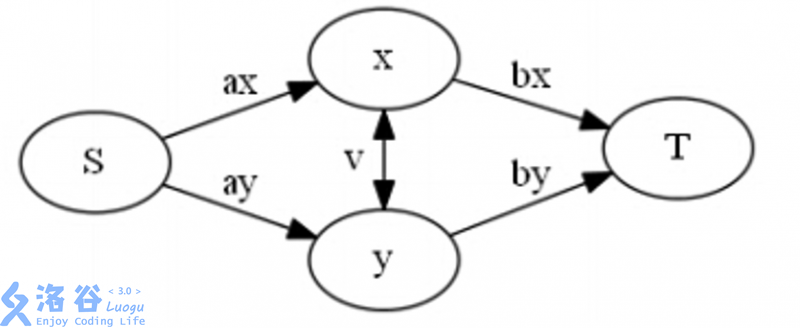
这里我们假设S集是$a_i$选0，T集是$a_i$选1。一开始我们获得了所有$b$的收益，我们要让损失最小化。

列式子

$(1)bx+by=c_x+c_y$ (都选1的时候只有$c$的损失)

$(2)ax+ay=b_{x,x}+b_{x,y}+b_{y,x}+b_{y,y}$ (都选0的时候损失为$b$数组)

$(3)ax+by+v=b_{x,x}+b_{x,y}+b_{y,x}+c_y$

$(4)ay+bx+v=b_{y,y}+b_{x,y}+b_{y,x}+c_x$ (一个选1一个选0时损失为$b$数组两数之间的收益和对应$c$数组收益)

可以解出对于每一组$(x,y)$

$ax=b_{x,x}+\frac{b_{x,y}+b_{y,x}}{2}$

$ay=b_{y,y}+\frac{b_{x,y}+b_{y,x}}{2}$

$bx=c_x$

$by=c_y$

$v=\frac{b_{x,y}+b_{y,x}}{2}$

对于每一组$(x,y)$,我们需要把割$ax$和$ay$的损失累加起来。

$ax=b_{x,x}+\frac{\sum_{i=1}^n(i!=x)b_{x,i}+b_{i,x}}{2}=\frac{\sum_{i=1}^nb_{x,i}+b_{i,x}}{2}$

这样建图就非常明显了，为了避免有小数的出现，我们将流量翻倍。

从源点$S$往每个点$i$连接流量为$b$数组第$i$行和第$i$列的权值总和的边。

每个点$i$往汇点$T$连接流量为$c_i*2$的边。

每一对点$(i,j)$之间连流量为$b_{i,j}+b_{j,i}$的双向边。

最后答案为$\sum_{i=1}^n\sum_{j=1}^nb_{i,j}-\frac{Maxflow(S,T)}{2}$

时间复杂度O($Maxflow(n,n^2)$)