自动搬运

查看原文

来自洛谷，原作者为

	Great_Influence **

搬运于2025-08-24 21:54:29，当前版本为作者最后更新于2018-01-03 20:11:44，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

迷之数论，证明比猜难。

首先，先猜一个结论：$2^k$的分组方式可以从$2^{k-1}$转移而来。

证明很简单。首先，分组要求可以转化为

$\forall i\in(0,n-1),\sum_{j\in S}j^n=\sum_{j\notin S}j^n$

其中S为其中一组。

先观察样例，可以发现，$2k+1$和$2k+2$都不在同一组内。于是，可以强行认为，这两个数一定不在同一组。那么上面的式子可以化为

$\forall i\in(0,n-1),$

$\sum_{2j+2\in S}(2j+2)^i-(2j+1-1)^i$

$-\sum_{2j+1\in S}(2j+1+1)^i-(2j+1)^i=0$

设$t=2j+1$(t为奇数)，在进行转化，可以发现：

原式左边

$=\sum_{t+1\in S}(t+1)^i-t^i$

$-\sum_{t\in S}(t+1)^i-t^i$

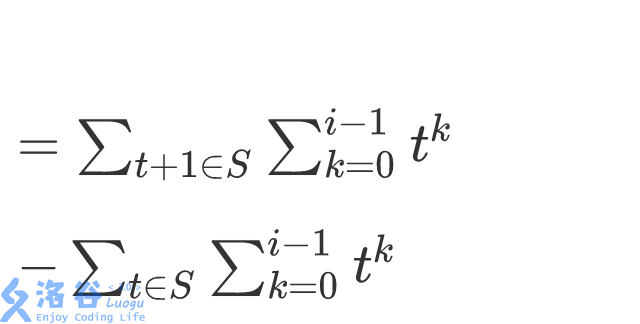
分析这个式子，发现除了最后一项1以外，其他几项就是i-1的要求，于是可以直接复制第i-1项的关系，在将第i-1项的关系在复制一遍并都加上$2^{i-1}$，序列交换后接到后边，即可满足要求。

设箭头表示2k+1和2k+2中的选择方向，$\uparrow$表示2k+2在集合S内,$\downarrow$表示2k+1在集合内，那么可以发现集合应该是长这样:

$\downarrow\uparrow\uparrow\downarrow\uparrow\downarrow\downarrow\uparrow......$

分析可以发现，若$2^i$为小于k最大的2的整次幂，则第$k$个箭头和第$k-2^i$个箭头是反向的。那么就对于每个询问暴力处理所在箭头的方向。注意处理出方向后，还要根据奇偶来判断是箭头还是箭尾。时间复杂度$O(qlog_2n)$。

代码：

    #include<bits/stdc++.h>
    #include<cctype>
    #define For(i,a,b) for(i=(a),i##end=(b);i<=i##end;++i)
    #define Forward(i,a,b) for(i=(a),i##end=(b);i>=i##end;--i)
    #define Rep(i,a,b) for(register int i=(a),i##end=(b);i<=i##end;++i)
    #define Repe(i,a,b) for(register int i=(a),i##end=(b);i>=i##end;--i)
    using namespace std;
    template<typename T>inline void read(T &x){
        T s=0,f=1;char k=getchar();
        while(!isdigit(k)&&k^'-')k=getchar();
        if(!isdigit(k)){f=-1;k=getchar();}
        while(isdigit(k)){s=s*10+(k^48);k=getchar();}
        x=s*f;
    }
    void file(void){
        #ifndef ONLINE_JUDGE
        freopen("water.in","r",stdin);
        freopen("water.out","w",stdout);
        #endif
    }
    static int n,q;
    void work()
    {
        read(n);
        read(q);
        static long long k,j;
        static bool is;
        Rep(i,1,q)
        {
            read(k);j=1;is=k&1;k=(k+1)>>1;
            while(j<=k)j<<=1;
            while(k>1)
            {
                while(j>=k)j>>=1;
                is^=1;k-=j;
            }
            printf("%c\n",is?'X':'Z');
        }
    }
    int main(void){
        file();
        work();
        return 0;
    }
（题解比代码难打多了，题目想了10多min，题解打了将近30min。。。。。。）