自动搬运

查看原文

来自洛谷，原作者为

	吾乃会虎 建议使用Math/MC/Furry诱捕

搬运于2025-08-24 21:54:21，当前版本为作者最后更新于2018-12-13 15:58:22，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

用此篇题解纪念我已经被忘却的关于这个题目的一篇题解

甚至也被洛谷遗忘在回收站里了

首先我们要看到大佬的题解

所有大佬（包括管理员大大发的题解）都点出了一个重点： —— 父亲和儿子的标号都相差一个斐波那契数

看起来这是一个不知道原因的规律，实际上这是可以被证明的（不想看证明的可跳过）

首先显而易见的是，前几轮的兔子中每一轮有$F_{N+1}$只兔子，要生$F_N$只兔子，也符合“父亲和儿子的标号都相差一个斐波那契数”这一条件

然后如果第$N$轮的兔子符合条件，那么此时会有$F_{N+1}$只兔子，还要生$F_N$只兔子

由于每一轮的兔子编号是按父亲的编号大小编的，所以$1$号兔子会多一个$F_{N+1}+1$号的儿子，$2$号兔子会多一个$F_{N+1}+2$号的儿子……$F_{N+1}$号兔子会多一个$F_{N+1}+F_N$号兔子，其中父亲与儿子的编号都相差$F_N$

而此时，原来$F_{N+1}$只兔子都已经“长大成兔”了，就可以再生$F_{N+1}$只兔子，兔子总数也由$F_{N+1}$只兔子变为了$F_{N+1}+F_N=F_{N+2}$只兔子，也符合前提，因此，第$N+1$轮时条件也成立

通过数学归纳法，我们证明了这个规律

然后介绍一下“斐波那契编码”（我更喜欢叫做“斐波那契进制”）

百度百科：斐波那契编码——百度百科

好，结束了 捕捉极其不想打字的蒟蒻一枚

最后来看一下我的蒂花之秀的解法

首先我们要记住一个方法：对带编号的数论问题，把编号改成由$0$起始对结果可能有意想不到的惊喜和AK比赛的更大的惊喜

我们来试试这个方法：

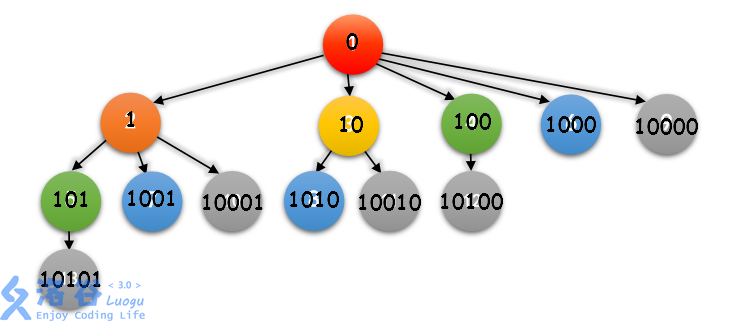
是不是发现了什么？好像每一个父亲都是儿子的后缀？

其实这很好解释

每一只兔子都和他的父亲相差一个斐波那契数，在出生轮数也会相差至少两轮，这就相当于说每一只兔子的编号都是它的父亲的编号+一个不会产生进位的斐波那契数，在编号上就表现为父亲编号是儿子编号的前缀

所以说，我们只要知道一个数的编号，就可以知道它的所有祖先的信息，最后只要暴力匹配就可以了，编程难度瞬间减小但思维难度比原来更高了

最后附代码：

#include<bits/stdc++.h>
using namespace std;
template<typename type>
type get(type &out){
	type sign=1,num=0;
	char input='\0';
	bool over=false,finds=false;
	while((input=getchar())<=32);
	do{
		switch(input){
			case '+':sign=-sign;
			case '-':sign=-sign;
	  					if(!finds)
	  						finds=true;
	  					else
	  						over=true;
	  			break;
	  		case '0':case '1':case '2':case '3':case '4':
	  		case '5':case '6':case '7':case '8':case '9':
	  					num=num*10+(input^48);
	  			break;
	  		default:
				over=true;
				break;
		}
	}while((input=getchar())>32&&!over);
	return out=sign*num;
}//并没有什么卵用的快读
template<typename type>
type put(const type &in){
	type sign=1;
	if(in<0)sign=-sign,putchar('-');
	if(in*sign>=10)put(in*sign/10);
	putchar((in*sign%10)^48);
	return in;
}//比快读更没卵用的快输
const long long MAXN=300000;
long long FBNQ[70]={0,1,2};
long long A[70],B[70];
int main(){
	for(int i=3;i<60;++i)
		FBNQ[i]=FBNQ[i-1]+FBNQ[i-2];
    //将斐波那契数初始化
	int n=0;
	get(n);
	while(n--){
		long long a=0,b=0,ans=1;
		get(a),get(b);
        //输入数据
		--a,--b;
        //将编号改成从0开始
		for(int i=59;i>0;--i)
			A[i]=a/FBNQ[i],a%=FBNQ[i];
		for(int i=59;i>0;--i)
			B[i]=b/FBNQ[i],b%=FBNQ[i];
        //将编号化成斐波那契进制
		for(int i=0;i<60;++i,ans+=FBNQ[i]*A[i])
			if(A[i+1]!=B[i+1])
				break;
        //强行匹配
		put(ans);putchar('\n');
        //输出答案
	}
	return 0;
} 

时间复杂度$O(Mlog_\Phi N)$ 空间复杂度$O(log_\Phi N)$

效果近似于LCA的解法，但是代码难度小，常数也小一些

最后的闲言

实际上我当时一开始想的也是LCA，但是我太蒟了，不会这些解法，于是发现了数论解法

所以说，蒟蒻也是有春天的~~（滑稽）~~