1 条题解
-
0
自动搬运
来自洛谷,原作者为

4BboIkm7h
我们邦多利的紫毛双马尾鼓手都这么强的吗搬运于
2025-08-24 21:53:51,当前版本为作者最后更新于2025-08-18 16:13:49,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
题意
给定一个半径为 ,圆心在原点的圆,再给定 个点的坐标 。这些点构成一个图,任意两点之间有连边,当且仅当两点所在直线与圆相离,求图的最大团的团数(最大完全子图的顶点数)。
数据范围:
分析
一开始我并不知道最大团是什么,但是发现可以 建图,于是我就去搜了一下最大团问题有没有快速的解决方法,然后发现这玩意 ,于是建图跑最大团的方法直接被肘飞。
这题实际上是一个套着几何外皮的最长上升子序列问题。
考虑除了到圆心的距离,还有哪些刻画线圆位置关系的方式。我们知道从圆外一个点引出圆的双切线,两个切点就能把圆分成两段圆弧,以下称这两段圆弧中任意一段为圆外一点的“对应圆弧”。
不难发现以下对应关系:- 线段所在直线与圆相离 线段端点的对应圆弧有重合部分,但不存在包含关系。
- 线段所在直线与圆相切 线段端点的对应圆弧可以接在一起。
- 线段所在直线与圆相交 线段端点的对应圆弧没有重合部分。
现在我们的问题变成:找到最多的一组点,使它们的对应圆弧两两有重叠但不存在包含关系。把圆剪开拉成一条线段,那么一段圆弧可以看作一个区间。由于两个切点分开的两段圆弧是等价的,所以不用担心有的弧会被剪开,因为只需要取另外与之等价的那段弧就可以了。最后要解决的问题形式化为:
对于区间集合 ,找到最大的一个子集 ,使得 $\forall A,B \in S, A\cap B \neq \varnothing, A \nsubseteq B, B \nsubseteq A$。
将所有区间按左端点为第一关键字,右端点为第二关键字排序,枚举每一个区间 作为区间集合 的起点,将所有满足 的 加入 ,那么 中右端点的最长上升子序列长度就是 ,也就是钦定 必选时的答案,最终问题的答案为所有情况的最大值。
最后,我们回过头来看看如何将每个点的对应圆弧映射成区间。考虑以圆心到切点的射线的旋转角(弧度制)作为区间的端点。设 为圆心到该点 射线的旋转角,这条射线与切半径的夹角为 ,那么对应圆弧映射区间就是 。
$$\varphi=\arccos\frac{r}{\sqrt{x^2+y^2}},\theta=\arctan \frac y x(x\neq 0) $$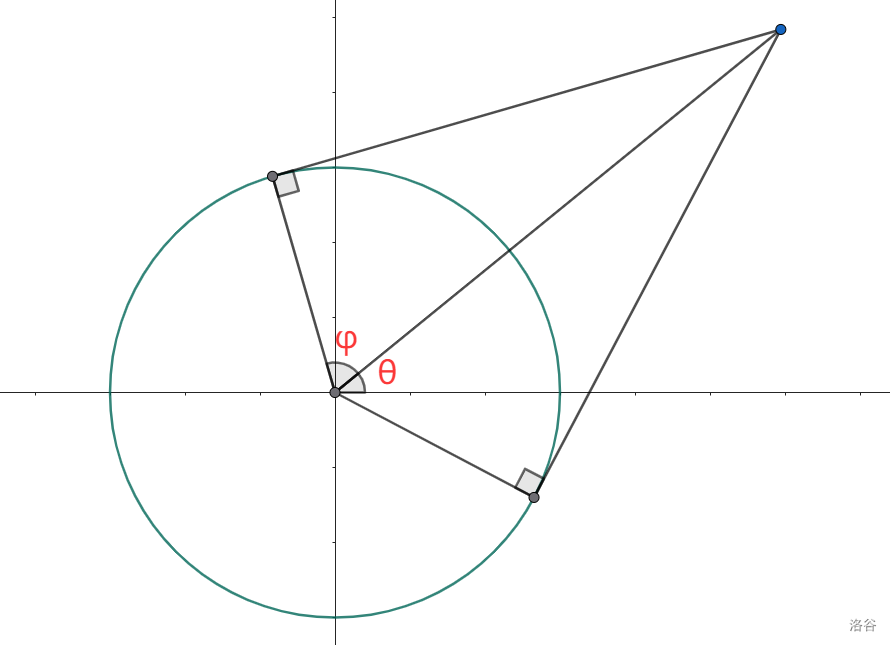 由简单几何知识不难得到:
由简单几何知识不难得到:为了能够处理 的情况,我们在程序中使用
atan2(y,x)函数。反余弦函数正常使用acos()即可。最后还需要把端点全都调整到 或 内。代码
时间复杂度:。
#include<bits/stdc++.h> #define L first #define R second using namespace std; const int N = 2e3 + 10; const double pi = acos(-1.0); inline int read(){ int x = 0, neg = 1; char c = getchar(); while(!isdigit(c)) {if(c == '-') neg = -1; c = getchar();} while(isdigit(c)) {x = (x << 1) + (x << 3) + (c ^ 48); c = getchar();} return x * neg; } int n, r, len, ans; double mn[N]; vector<double> a; pair<double, double> q[N]; int main(){ n = read(), r = read(); for(int i = 1; i <= n; i++){ int x = read(), y = read(); double mid = atan2(y, x), dta = acos(r / hypot(x, y)); double L = mid - dta, R = mid + dta; while(L < -pi) L += 2 * pi; while(R >= pi) R -= 2 * pi; if(L > R) swap(L, R); q[i] = make_pair(L, R); } sort(q + 1, q + n + 1); for(int l = 1; l <= n; l++){ a.clear(); a.push_back(q[l].R); for(int i = l + 1; i <= n; i++) if (q[i].L <= q[l].R && q[i].R >= q[l].R) a.push_back(q[i].R); mn[len = 1] = a[0]; for(int i = 1; i < a.size(); i++){ if(a[i] > mn[len]) mn[++len] = a[i]; else *lower_bound(mn + 1, mn + len + 1, a[i]) = a[i]; } ans = max(ans, len); } printf("%d", ans); return 0; }
- 1
信息
- ID
- 2854
- 时间
- 2000ms
- 内存
- 500MiB
- 难度
- 6
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
