自动搬运

查看原文

来自洛谷，原作者为

	LeavingZzz 生当如夏花绚烂，死当如秋叶静美

搬运于2025-08-24 21:53:32，当前版本为作者最后更新于2020-04-28 22:28:26，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

Solution For P3866

$\large\mathcal{By\text{ }ShadderLeave}$

感觉另外两篇题解只讲了实现方法QwQ
那我来口胡一下思维历程
Upd On 2020-5-4：题解界面改了代码缩进又鬼畜了

$\mathsf{Link\text{ }To\text{ }Problem}$
$\color{red}\mathsf{A\text{ }Better\text{ }Reading\text{ }Experience}$

题目分析

这道大意是让我们把敌军封在一个区域内不能逃到边界，实际上就是想让我们切断从敌军当前位置到边界的道路，在这个基础上使用最小的花费。
画个图大概yy一下就是：

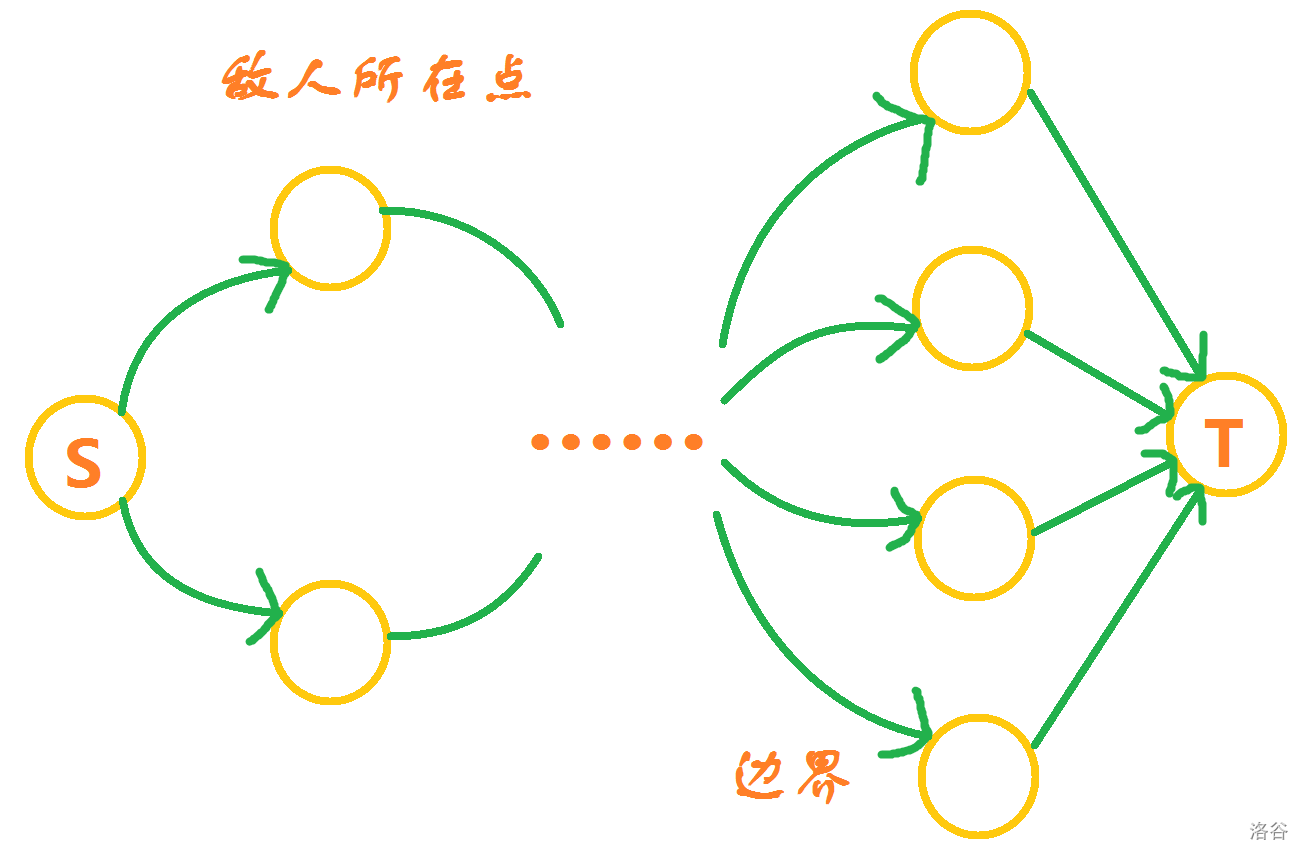
中间可能较复杂的部分先不想，我们就是想把 $S$ 和 $T$ 之间使用最小的代价砍断使二者不可达（建立超级源点和超级汇点是因为可能有多支敌军，同时边界的点也不止一个）。
这就很自然地想到了网络流的最小割。

中间部分怎么办呢？

中间的部分要表示原图的联通情况，同时要能够表现切断某些点的代价，如果直接用朴素的方法：假如两点 $u$、$v$ 相邻，就建立边 $(u,v)$ ,权值为点 $v$ 的点权的一条边，是会有bug的（比如一个点炸两次）。

那么我们使用一个小技巧：拆点法。

将一个点 $u$ 拆成一个入点 $u_1$ 以及一个出点 $u_2$,并且在 $u_1$、$u_2$ 之间连一条边，权值为点 $u$ 的点权，这样破坏掉点 $u$ 就相当于切断 $u_1$ 和 $u_2$ 之间连的一条边，切断后所有想通过 $u$ 点的路径会被阻断。

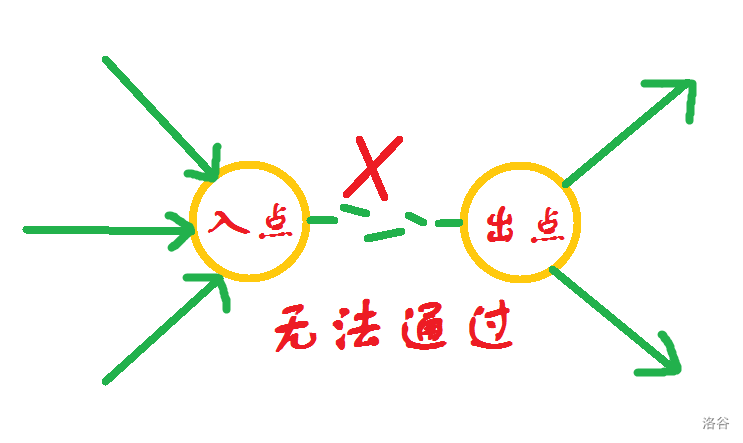
所以这时候模型基本浮出水面：

1. 建立超级源点并且和所有的敌军点的入点连接
2. 将所有的边界点的出点连接到超级汇点
3. 对于中间的点，每个点的出点连接到相邻点的入点

接下来是边权的问题

已经说过每个点的入点和出点之间的边的边权是该点的点权，假如该点是敌人 则不用连边（因为连边表示可以炸掉这一点，不合题意），假如该点已经是障碍，那么更不用连边，而且在相邻点连边的时候也要滤掉这个情况（本来就不是联通的多连边浪费时空）。

对于相邻点间的边，是不可以断掉的，因为断掉这条边没有实际的意义，它只是用来表示连通性的，断掉就会破坏原图的信息，防止它被断掉就将其边权置为 $inf$。（最小割选中正无穷的边就不会是最小割了）

对于超级源汇点和具体点之间的连边，同样不可以断掉，置为 $inf$。

由最小割最大流定理，最小割在数值上等于最大流，直接跑最大流即可。

说完啦。要是还有问题就去代码里面找我吧qwq

$\large\mathsf{Code}:$

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
queue <int> q;
const int maxn=1807;//想想自己数组开没开小
const int maxm=40007;
const int inf=0x7f7f7f7f;
int N,M,S,T,all;
struct E{
    int u,v,cf;
}e[maxm];
int first[maxn],nt[maxm],ES=1;//边的编号初始化否则反边不可表示为 i^1
#define cf(i) e[i].cf
inline void addE(int u,int v,int cf)
{
    e[++ES]=(E){u,v,cf};
    nt[ES]=first[u];
    first[u]=ES;
    return ;
}
inline void add(int u,int v,int cf)//网络瘤专用加边
{
    addE(u,v,cf);addE(v,u,0);
    return ;
}
inline int R()
{
    char c;
    int re,f=1;
    while((c=getchar())>'9'||c<'0')
    if(c=='-') f=-1;
    re=c-48;
    while((c=getchar())>='0'&&c<='9')
    re=re*10+c-48;
    return re*f;
}
int cnt[maxn],cur[maxn];
inline bool BFS()//Dinic算法
{
    int u,v;
    memset(cnt,0,sizeof(cnt));
    cnt[S]=1;q.push(S);
    while(!q.empty())
    {
        u=q.front();q.pop();
        for(register int i=first[u];i;i=nt[i])
        {
            v=e[i].v;
            if(!cnt[v]&&cf(i)>0)
            {
                cnt[v]=cnt[u]+1;
                q.push(v);
            }
        }
    }
    return cnt[T]!=0;
}
inline int min_(const int &x,const int &y) {return x<y?x:y;} 
inline int dfs(int u,int f)//Dinic算法
{
    if(u==T) return f;
    int v,d,sum=0;
    for(register int &i=cur[u];i;i=nt[i])
    {
        v=e[i].v;
        if(cnt[v]==cnt[u]+1&&cf(i)>0)
        {
            d=dfs(v,min_(f,cf(i)));
            if(d>0)
            {
                sum+=d;f-=d;
                cf(i)-=d;cf(i^1)+=d;
                if(f<=0) return sum;
            }
        }
    }
    return sum;
}
int m[37][37];
inline int num(int i,int j)//由坐标换算成的点编号
{
    return (i-1)*M+j;//要减一，切记！！切记！！
}
int main()
{
	N=R();M=R();all=N*M;//总点数
	T=2*all+1;
    for(register int i=1;i<=N;i++)
        for(register int j=1;j<=M;j++)
            m[i][j]=R();
    for(register int i=1;i<=N;i++)
        for(register int j=1;j<=M;j++)
        {
			if(m[i][j]==-1) continue;//本来就是障碍啥也不用做
			else if(m[i][j]==0)//特判敌军
				add(num(i,j),num(i,j)+all,inf),add(S,num(i,j),inf);
			else add(num(i,j),num(i,j)+all,m[i][j]);
			//相邻点之间的连边
			if(i>1&&m[i-1][j]!=-1) add(num(i,j)+all,num(i-1,j),inf);
			if(j>1&&m[i][j-1]!=-1) add(num(i,j)+all,num(i,j-1),inf);
			if(i<N&&m[i+1][j]!=-1) add(num(i,j)+all,num(i+1,j),inf);
			if(j<M&&m[i][j+1]!=-1) add(num(i,j)+all,num(i,j+1),inf);
			//特判边界
			if(i==1||j==1||i==N||j==M) add(num(i,j)+all,T,inf);
        }
    int ans=0;
    while(BFS())//Dinic求 最大流/最小割
    {
        memcpy(cur,first,sizeof(first));//当前弧优化
        ans+=dfs(S,inf);
    }
    printf("%d",ans);
    return 0;
}

如果这篇题解对您有帮助，请点个赞QwQ
如果还有问题可以评论或者直接私信窝。
蟹蟹管理大大审核^_^

$\LARGE\mathcal{The\text{ }End}$