1 条题解
-
0
自动搬运
来自洛谷,原作者为

天泽龟
理想与孤独 | My Blog: http://tzturtle.moe搬运于
2025-08-24 21:53:32,当前版本为作者最后更新于2019-09-26 17:48:25,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
翻了很多题解没找到一篇详细图解,于是就有了这篇。
表还是很需要一篇带图解的题解吧, 定义啥的其他题解都有,就不赘述了,我们直接结合图例来理解代码。
-
预处理阶段。
- 首先你应该知道的是,ST表是利用倍增思想来缩短时间的。而倍增就体现在他数组的定义中:对于,指的是在序列的第i项,向后个元素所包含序列间的最大值。
对于,我们可以画出这么一个图,其下标即为:
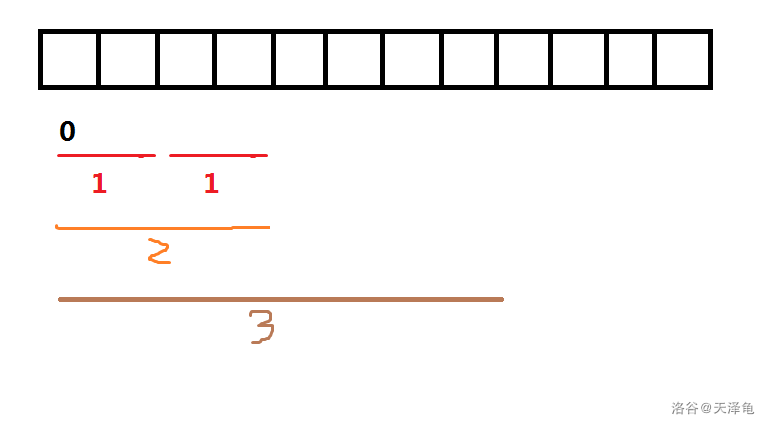
那么对于当前转移其实很明显了,我们可以直接考虑将两个小区间的答案合并,即为这个大区间的值;如图中即可由转移来。
其中也可写为,这里位运算会更方便也会更快。
这个式子告诉我们,ST表类似于区间DP,是由两个小区间合并上来的。所以应该先枚举区间长度l(这里即为),再枚举.
- 然后一个问题应运而生了:我们这个转移方程有没有边界呢?
不妨来看一下的图:
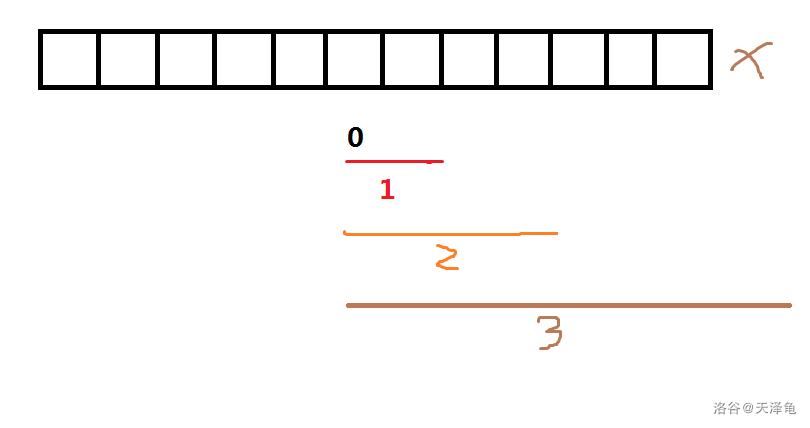
可以看出在时,的范围是,已经超出了我们数据的范畴。所以当时,只能取到
由上例再根据转移方程,不难看出当确定时,i的范围受限在。
那么又根据的情况,可知应满足:
,其中表示n关于底数2的对数向下取整,可以递推求得。
最终附上预处理代码:
scanf("%d%d",&n,&m); lg[1]=0; for (int i=2;i<=n;i++) lg[i]=lg[i>>1]+1; //求lg[i]函数。 for (int i=1;i<=n;i++) scanf("%d",&f[i][0]); for (int j=1;j<=lg[n];j++) for (int i=1;i<=n-(1<<j)+1;i++){ //注意两个边界 f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]); }时间复杂度为
-
求最值阶段。
我们现在来求红色标记区间的最值。如果要最大化利用ST表,仍应该考虑类似处理ST表的方法,将该区间分成 两个ST表可直接维护的小区间,然后二者求最值即可。
- 那对于起始点,我们找一段ST表在该区间内可覆盖的,最大的子区间,由数学语言可描述为:
那我们直接取等,令即可~
于是对于起始点点在ST表里的取值即为:
- 对于终止点,我们反向找一个与起始点要求相同的子区间,由于对称性,此时k仍为起始点求得的
但是我们应该如何确定该子区间的起点呢?由于子区间长度为,设起点在处,则满足:
于是对于终止点在ST表里的取值即为:,可证明这样一定可以覆盖整个区间。
综上,对于区间求其最值,不难发现答案即为:
接下来是一个例子:
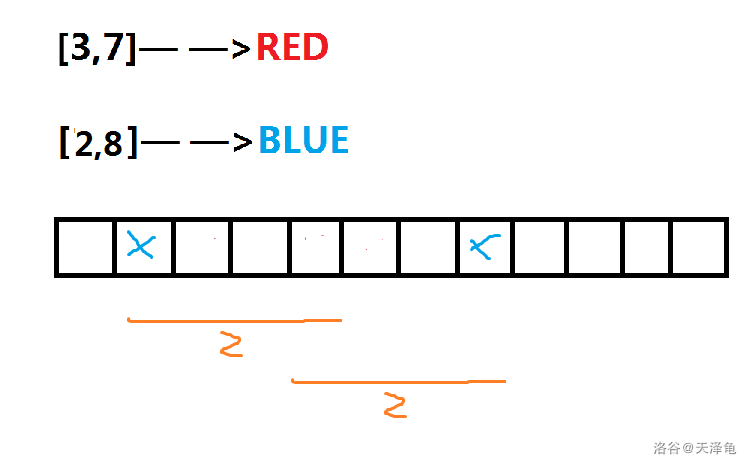
对于蓝色区间,我们先找到,则两个子区间即为:,对应了,两个取最值即可。
附上求值部分代码:
for (int i=1;i<=m;i++) { cin>>x>>y; int l=lg[y-x+1]; cout<<max(f[x][l],f[y-(1<<l)+1][l])<<endl; }-
后记
虽说是详细图解,但好像更偏向于一些简单的数学证明。。
ST表对于RMQ问题还是有很大的使用空间,希望各位能好好掌握。
最后附上我丑陋的代码:
#include <iostream> using namespace std; int n,m,x,y,a[100010],lg[100010],f[100010][20]; int main() { cin>>n>>m; lg[1]=0; for (int i=2;i<=n;i++) lg[i]=lg[i>>1]+1; for (int i=1;i<=n;i++) cin>>f[i][0]; for (int j=1;j<=lg[n];j++) for (int i=1;i<=n-(1<<j)+1;i++){ f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]); } for (int i=1;i<=m;i++) { cin>>x>>y; int l=lg[y-x+1]; cout<<max(f[x][l],f[y-(1<<l)+1][l])<<endl; } } -
- 1
信息
- ID
- 2824
- 时间
- 800ms
- 内存
- 125MiB
- 难度
- 3
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
