自动搬运

查看原文

来自洛谷，原作者为

	MloVtry **

搬运于2025-08-24 21:53:29，当前版本为作者最后更新于2017-09-21 19:10:18，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

虽然月赛题有官方题解但是空荡荡的不是很难看吗。。。

这个题显然是有规律的啦….虽然我的方法并不是很好

首先我们来看看

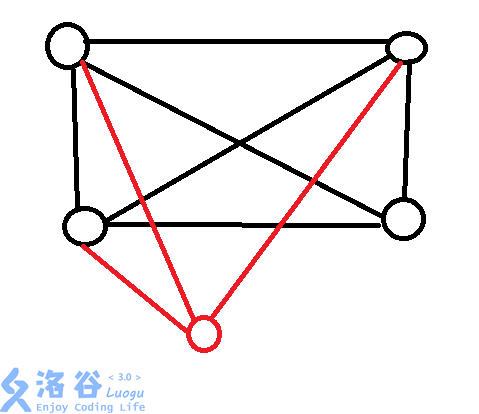
对于5去掉一条边，我们能够发现，这是一个四个点的完全图加上一个点引出三

条边

那么，四个点的完全图有的环，这个图也一定有；而这个图比4点完全图多出来

的环，一定要经过第五个点（红的那个）。

为了形成环，肯定是一边进，一边出，选择有C(3,2)种，而任意一种选择，肯定要落在4点完全图的两个点上，所以我们还要知道四个点的完全图中从任意A开始到任意B有几种方案

可以数出来，是5

用it[i]，表示i个点的完全图，任取A、B，A->B的方案数有多少

last[i]，表示i个点的完全图，有多少个环

那么 ans[n]=c(n-2,2)*it[n-1]+last[n-1]

到这里，60%已经可以解决了

接下来是AC

用计算器可以发现一个事情，剩下的40%只有100W的范围

所以…我们可以预（打）处（表）理一下

然后…就可以A了…

关于it以及last的推导关系。。。我并不会证明，但是通过样例可以推出来一个不知对错的式子，这时候就要看胆子了2333333

#include<iostream>
#include<cstdio>
#define mod 998244353
#define M 999000000-2
#define ll long long
using namespace std;
ll T,n;
ll c[100021],it[100021];
ll last[100021];
void get_c()
{
    c[2]=1;
    for(ll i=3;i<=100020;i++)
    {
        c[i]=(i-1)*i/2;
        c[i]%=mod;
    }
    it[3]=2;
    for(ll i=4;i<=100020;++i)
    {
        it[i]=it[i-1]*(i-2)+1;
        it[i]%=mod;
    }
    last[3]=1;
    for(ll i=4;i<=100020;++i)
    {
        last[i]=c[i-1]*it[i-1]+last[i-1];
        last[i]%=mod;
    }
}
ll cb[1000010],lastb[1000010],itb[1000010];
void get_b()
{
    cb[0]=1420232,lastb[0]=876466444,itb[0]=141309211;
    ll to=1000005;
    for(ll i=1;i<=1000005;++i)
    {
        ll num=i+M;
        cb[i]=cb[i-1]+num-1;
        cb[i]%=mod;
        lastb[i]=cb[i-1]*itb[i-1]+lastb[i-1];
        lastb[i]%=mod;
        itb[i]=itb[i-1]*(num-2)+1;
        itb[i]%=mod;
    }
}
int main()
{
    scanf("%lld",&T);
    get_c();
    get_b();
    while(T--)
    {
        scanf("%lld",&n);
        if(n>M)
        {
            n%=M;
            ll ans=cb[n-2]*itb[n-1]+lastb[n-1];
            ans%=mod;
            printf("%lld\n",ans);
            continue;
        }
        ll ans=c[n-2]*it[n-1]+last[n-1];
        ans%=mod;
        printf("%lld\n",ans);
    }
}
//今天也依旧没有捞到47岛风厌战呢