自动搬运

查看原文

来自洛谷，原作者为

	TDoG_W Ut puto Deus fio.Adeste,si quid mihi restat agendum.

搬运于2025-08-24 21:53:02，当前版本为作者最后更新于2024-03-09 16:45:35，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

题目历史地位

本题是 $\texttt{FJOI}$ 历年 「绝世唐问、逆天神题」 中的一道，自 2017 年以来全网搜不到满分题解。本题是 D2T2，据说当年考场上无人满分，最高 90PTS。测评记录里基本都是套数据得到 100PTS。名副其实的 「OI 界未解之谜」。

本篇题解应该是全网目前能搜到的第一篇满分正解。

附赠 $\texttt{FJOI}$ 唐问三剑客（不建议查看）

• [FJOI2015] 带子串包含约束LCS问题
• [FJOI2016] 所有公共子序列问题
• [FJOI2017] 回文子序列问题

关于子序列自动机

看到又是 $\texttt{FJOI}$ 的子序列问题，果断祭出子序列自动机。

考虑到本题的特殊性，这里重新介绍一下子序列自动机的构建与使用，它应该是最简单的自动机。

构建

子序列自动机（Subsequence Automaton，为防止和后缀自动机 SAM 名称冲突，简称 SSAM）实际上是一张子序列的 DAG，上面任意连续路径都是原串的一段子序列。

以下是一个例子，以FJOIAKIOI构建的子序列自动机：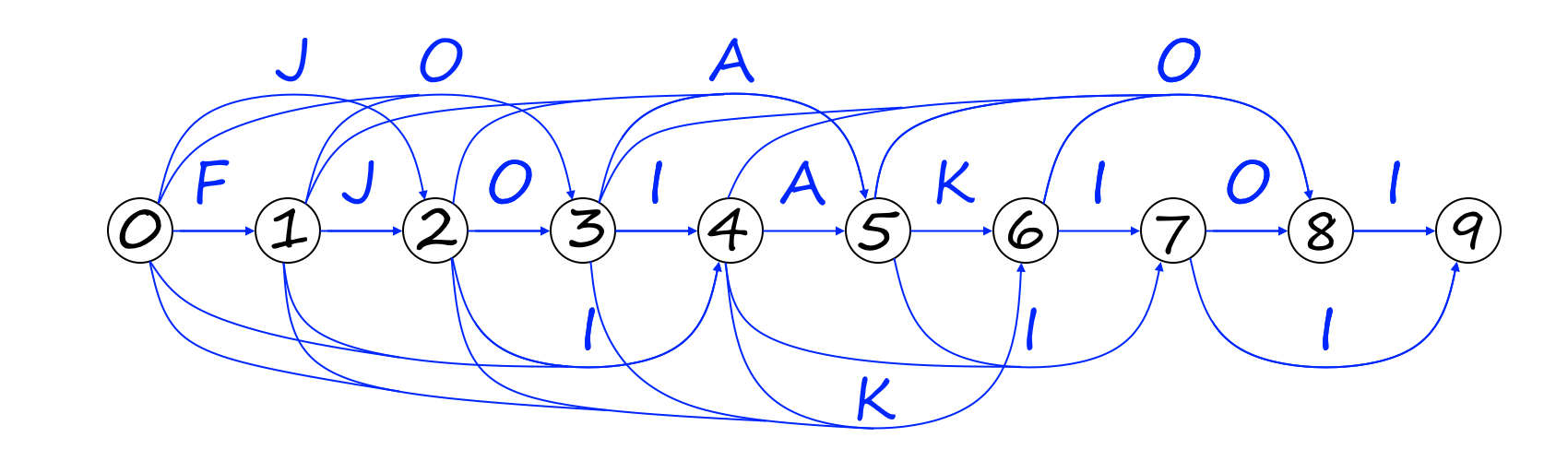

如图每条边指向的是自己之后第一个出现这个字符的位置，据此可以想到一种构建方法：构建时我们可以从尾部开始反向构建，每次复制上一次的所有边，修改上个字符的出现位置。

乍一看好像很乱？没事，接下来一步步梳理。

以下是构建过程（蓝边表示继承的边，红边表示修改的边）：

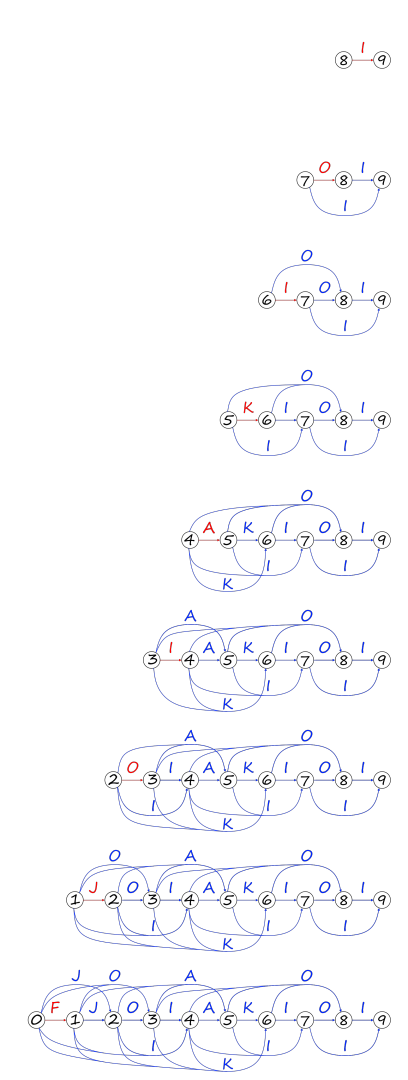
• Code

int Sub[N][M],tmp[M];

void build(int a[],int n,bool rev){
    memset(tmp,0,sizeof(tmp));
	for(int i=n;i>=1;i--){
		tmp[a[i]]=i;
		memcpy(Sub[i-1],tmp,sizeof(tmp));
	}
}

设有一串长 n,字符集为 $\Sigma$。

朴素构建 $\mathcal O(n \lvert \Sigma \rvert)$，单次查询 $\mathcal O(1)$。空间复杂度 $\mathcal O(n \lvert \Sigma \rvert)$。有时字符集较小，可以看成常数。

对于大型字符集，由于构建过程每个结点的连边最多只修改上一个结点连边的一条，实际上就是一个可持久化数组，主席树解决。

构建 $\mathcal O(n \log \lvert \Sigma \rvert)$，但单次查询退化至 $\mathcal O(\log \lvert \Sigma \rvert)$。空间复杂度 $\mathcal O(n \log \lvert \Sigma \rvert)$。

这个对解决本题帮助不大，不列代码了。

最长公共子序列

设有两串 $A,B$ 长度分别为 $n_1,n_2$，求它们的最长公共子序列。

这个问题现在就转化为了 $A,B$ 的子序列自动机的最长同构路径问题。使用动态规划解决，设 $f_{i,j}$ 为 $A$ 从 $i$ 出发，$B$ 从 $j$ 出发，能走的最长同构路径，设 $\Sigma_i$ 为结点 $i$ 的所有存在转移边字符的集合，设 $Sub_{i,k}$ 为从 $i$ 结点出发，向字符 $k$ 的转移边行走所到达的结点编号。综上，易得出转移式：

$$f_{i,j}=\max\limits _{k\in{\Sigma_i \cap \Sigma_j}}f_{Sub_{i,k},Sub_{j,k}}+1 $$

答案就是 $f_{0,0}$，这里笔者用记忆化搜索实现，为了方便实现记忆化，所有答案加了一，最终需要减去。这里 $m$ 是字符集大小。

int dfs(int x,int y){
	if(f[x][y])return f[x][y];
	f[x][y]=1;
	int u,v;
	for(int i=0;i<m;i++){
        u=SubA[x][i],v=SubB[y][i];
		if(!u or !v)continue;
		f[x][y]=max(f[x][y],dfs(u,v)+1);
	}
	return f[x][y];
}

ans=dfs(0,0)-1;

时间复杂度 $\mathcal O(n_1 n_2 \lvert \Sigma \rvert)$

对于更广义的最长公共子序列问题：$m$ 个串的公共子序列，时间复杂度 $\mathcal O(\lvert \Sigma \rvert \prod^m_{i=1} n_i )$。其中 $n_i$ 为 $i$ 号串的长度。

例题：[TJOI2008] 公共子串 （三串公共子序列问题）

最长回文子序列

设有一串长 $n$，求其最长回文子序列。

对原串的正反串分别建子序列自动机，跑最长公共子序列。

时间复杂度 $\mathcal O(n^2\lvert \Sigma \rvert)$

解题过程

那么本题非常明显了，对A、B串的正反串分别建子序列自动机，然后跑最长公共子序列。

同时发现字符集很大，但字符最多出现种数很少（最多只有 $2 \times 500$）。果断离散化。再加上状态数很多，有效状态很少，再使用 hash 表。

时间复杂度 $\mathcal O(n^4\lvert \Sigma \rvert)$。这个上界很松，跑不满。

然而笔者因为实现方式，被卡成 50PTS。

（接下来是笔者的漫长卡常之路）

终于卡到了 90PTS，此时笔者已经尝试无数种卡常方法。

实在没办法了，笔者开始考虑是不是算法本身有能优化的地方？

确实有，实际上笔者忽略了一个很关键的要点：「回文子序列」

回忆 Manacher ，猛然想到：实际上一个串自身的最长回文子序列只要比对一半就好了。这样最长回文子序列 $\mathcal O(n^2 \lvert \Sigma \rvert)$ 就还要再乘一个 $1 \over 2$的小常数！

这里是最长回文子序列的改进示例，注意要特判奇回文：

• Code

int dfs(int x,int y){
    if(x>n-y)return x==n-y+1;
	if(f[x][y])return f[x][y];
	f[x][y]=2;
	int u,v;
	for(int i=0;i<m;i++){
        u=SubPre[x][i],v=SubSuf[y][i];
		if(!u or !v)continue;
		f[x][y]=max(f[x][y],dfs(u,v)+2);
	}
	return f[x][y];
}

ans=dfs(0,0)-2;

那么 $\mathcal O(n^4 \lvert \Sigma \rvert) \rightarrow \mathcal O({1 \over 4} n^4 \lvert \Sigma \rvert)$，实际上比匹配四个串的最长公共子序列要快得多。

如果到这了，恭喜，$\texttt{FJOI}$ 绝世唐问已被解决。

代码

为防止贺题er，代码放 Record 里。

极小概率（纯整活，仅供娱乐）：

后记

实际上笔者绕的弯路比此处展示的多得多，例如尝试卡光速读、手写 hashmap、玄学优化等等。感兴趣的可以看笔者的几页测评记录。

目前本题终于有满分题解了，可喜可贺。

如果本篇题解对您有帮助，请点个赞再走吧！如果没有帮助，也可以看在笔者幸苦写题解的份赏个赞吧！ （也可以关注笔者嘤QWQ）

$\red{最后，警示后人：如果你看见 \texttt{FJOI} 打头的题，请不要尝试去做。}$