1 条题解
-
0
自动搬运
来自洛谷,原作者为

灵乌路空
已退役 | 东方众OIer交流群 (幻想乡养老院) : 691090556搬运于
2025-08-24 21:52:50,当前版本为作者最后更新于2019-07-15 21:30:41,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
先无良宣传一下博客
文章列表 - 核融合炉心 - 洛谷博客
知识点 : 优化 , 单调队列
-
题意:
有一个 大小的矩阵
部分矩阵中的点 带有价值
可以选择第一行 , 任何一个位置作为起点 .对于当前的位置 (表示在第 行第 列)
可以转移到: 中任意一个点
并且获得当前所在点的价值 .求 : 可以取得的 最大价值和
样例解释:
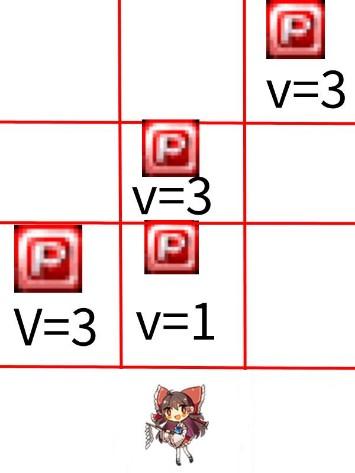
1.灵梦从 出发 : 总价值 , 现在为
2.灵梦转移到 : 总价值 ,现在为
3.灵梦转移到 : 总价值 ,现在为
故 , 总价值为
-
分析题意:
很显然 这是一道
状态转移方程 极其简单 :
用 表示在点 能到达的最大价值和 , 则有: $f[i][j] = max(f[i-1][k]) + v[i][j]\ ,\ (k\in [j-T , j+T]\ )$- 暴力:
直接枚举所有点 , 再枚举能转移到他的点 ?
复杂度 级别 ,
到手
考虑优化 :
- 可知:
第 行上点的 , 只与第 行有关
则可将每相邻的两行 , 单独拆分出来考虑 :
如图:
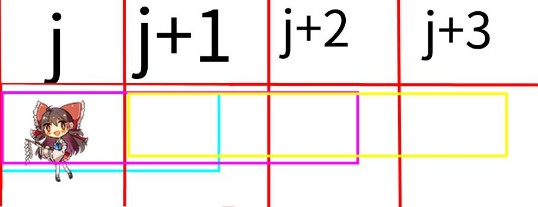
可以发现 :
-
转移到 点 的点 ,
为 行 , 区间 中 , 最大的点 -
转移到 点 的点 ,
为 行 ,区间 中 , 最大的点 -
转移到 点 的点 ,
为 行 ,区间 中 , 最大的点
后两个区间 ,
都可以通过 上一个区间 右移一个单位 得到
这不禁让我们想到了另一道题 : P1886 滑动窗口
如果您还未学习过单调队列 , 推荐这篇文章:
【洛谷日报#9】 [Sweetlemon] 朝花中学OI队的奋斗历程——浅谈单调队列这种 滑动窗口型 最值问题 ,
显然 , 可以通过 单调队列 来进行维护 .由上 , 我们便找到了一种合适 优化方法: 单调队列优化.
- 暴力:
-
算法实现:
假设,现在已经更新到第 行 :
- 先初始化单调队列 ,
将能够更新 的点 ,
加入单调队列 - 开始循环 , 更新 中每一个点 :
- 将能够转移到 的最右侧一个点 , 加入队列
- 使用单调队列找到能够转移到 的点的最大
- 用最大的 更新
- 清空单调队列 , 外层循环进入下一层 ,更新第 行
最后找到最后一行中 ,
最大的 ,
即所求最值 . - 先初始化单调队列 ,
上代码:
由于使用了手写数组模拟队列 ,
清空时只需重置头尾指针 , 及队首元素即可 .
常数吊打#include<cstdio> #include<ctype.h> #include<cstring> #define int long long #define max(a,b) a>b?a:b //===================================== const int MARX = 4e3+10; int n,m,k,t, now,ans; int f[MARX][MARX]; int head=1,tail=1;//手写双端队列 int q[MARX]={9223372036854775807};//为q[0]赋一个极大值,来防止插入元素时越界 //===================================== inline int read() { int fl=1,w=0;char ch=getchar(); while(!isdigit(ch) && ch!='-') ch=getchar(); if(ch=='-') fl=-1; while(isdigit(ch)){w=w*10+ch-'0',ch=getchar();} return fl*w; } void in(int x)//向单调队列中插入元素 { while(f[now-1][x]>f[now-1][q[tail]] && tail>=head) tail--;//取出队尾小于插入元素的数 , 以保证单调性 q[++tail]=x;//插入队尾 } int find(int x)//查询元素 { if(x+t<=m)in(x+t);//将能转移到x点 的 最后一个元素 x+t 插入队列 while(q[head]+t<x) head++;//找到队首第一个能够转移到x的点 return q[head]; } //===================================== signed main() { n=read(),m=read(),k=read(),t=read(); while(k--) { int x=read(),y=read(),w=read(); f[x][y]=w; } for(now=2;now<=n;now++)//从第二行,开始转移 { for(int i=1;i<=t;i++) in(i);//初始化单调队列 , 满足能够 转移j=1的点 for(int j=1;j<=m;j++) f[now][j]+=f[now-1][find(j)];// 进行转移 head=tail=1 , q[1]=0;//清空队列 } for(int i=1;i<=m;i++)//取得最大值 ans=max(ans,f[n][i]); printf("%lld",ans); }
完成了这篇题解 , 东方众信仰
-
- 1
信息
- ID
- 2761
- 时间
- 2000ms
- 内存
- 250MiB
- 难度
- 4
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
