1 条题解
-
0
自动搬运
来自洛谷,原作者为

离散小波变换°
有志不在年高,无志空长百岁搬运于
2025-08-24 21:52:42,当前版本为作者最后更新于2021-06-14 10:23:21,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
:修了一点排版。
题目大意
有一个 。现在挖去俯视图上 这一块(特别地,若 ,则是挖去 ),询问主视图中红色部分占可见部分的比例。
组数据。 且 。题解
前置知识
由于我们要求出看到的西瓜的面积,所以把切面转换到主视图非常重要。
令投射线通过点或其他物体,向选定的投影面投射,并在该面上得到图形的方法称为投影法。
考虑这样的图形:
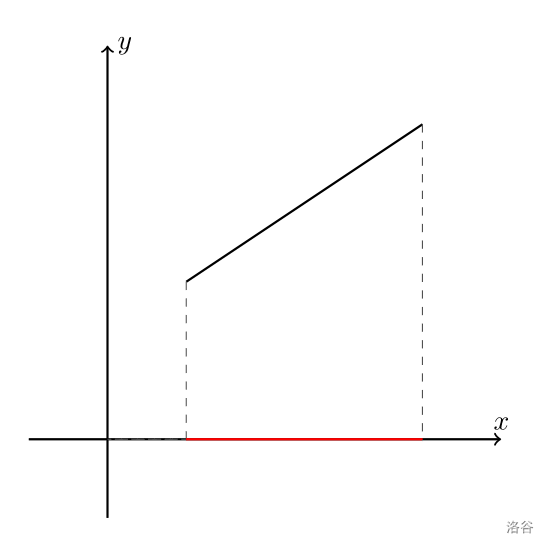
这就是一个非常简单的将直线投影到 轴上的例子。我们要做的就是把一个圆投影到平面上,并且计算出它的面积。关于投影,有一个非常重要的结论:投影后的图片的面积,就是投影前的面积乘上夹角的余弦值。显然这个结论对于矩形成立,而我们可以类比微分,把一个圆分成无数个矩形再分别投影。因此我们根据俯视图上,一个圆与主视图的夹角就可计算出这个圆在主视图上的面积。
此外,下文还会用到弧度制。在角度制里,一个完整的圆对应的度数是 ,而弧度制里这个值是 。将角度制转换为弧度制非常简单,对于角度制下的数值 ,转换为弧度制就是 。
在讨论各种复杂情况之前,我们先考虑一个更加简单的问题,也就是 的情况,并且我们仅考虑主视图右半部分。这种情况同样可以细分分为两类,每类三种。在下文中,我们认为西瓜的半径为 ,这显然不会影响答案。
- 第一类: 。观察下面三张图:
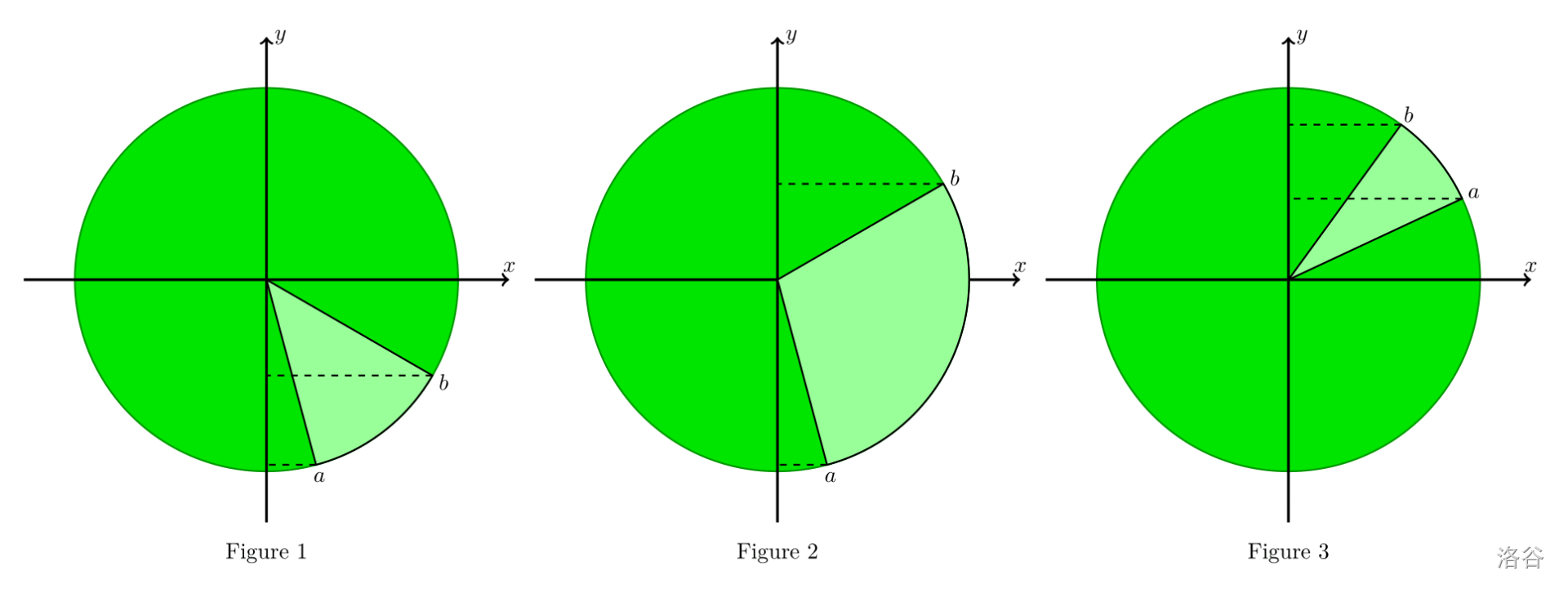
- 第一种情况, 。此时可视范围是 ,瓜瓢部分为 。
- 第二种情况, 。此时可视范围是 ,瓜瓢部分是 。
- 第三种情况, 。此时可视部分是 ,看不到瓜瓢。
- 第二类: 。同样地,有三张图:
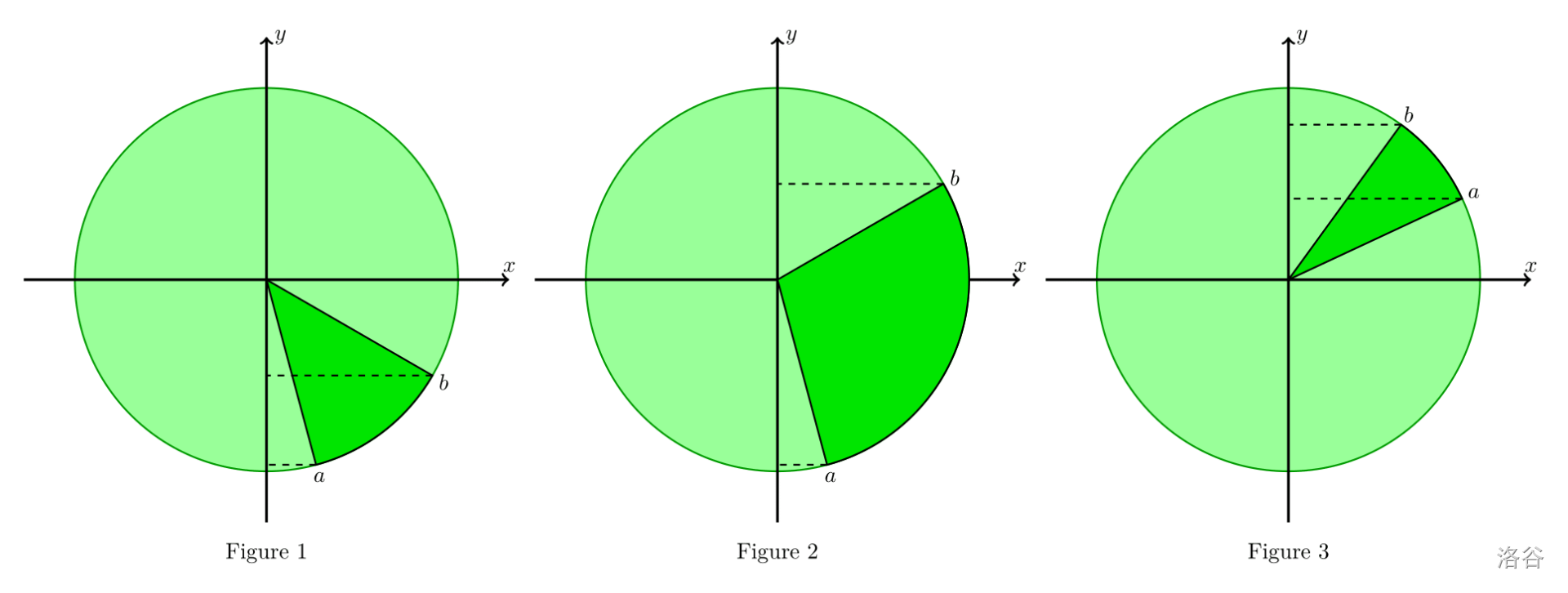
- 第一种情况, 。此时可视部分是 ,瓜瓢部分是 。
- 第二种情况, 。此时可视部分是 ,瓜瓢部分是 。
- 第三种情况, 。此时可视部分与瓜瓢部分相同,同样是 。
讨论完了这么多情况,快快封装到一个函数里吧。
显然,左半边的情况应当与右半边相似。我们只要想办法关于 轴翻转即可。一般地,对于左边的角度 ,翻到右边变成 ,应该有:
因此 。下面开始最终的讨论。
- 都在同一个半圆(即同在 或者同在 内)。这个时候,对于同时处在的半圆,直接套用刚刚的大讨论。如果 ,那么另外一个半圆可视部分就是 ,看不到瓜瓢;否则另外一个半圆无可视部分和瓜瓢部分。
- 在分别两个半圆当中。那么把这部分拆成两块,每块都相当于在一个半圆上挖去了一块,所以丢回刚刚的大讨论就行了。
参考代码
$$%偷偷藏个图片源码,没人发现吧 %\documentclass[UTF-8,border=10pt]{standalone} %\usepackage{listings,xcolor,tikz} %\usetikzlibrary{calc} %\newcommand{\suika}[2]{ % \filldraw[fill=green!40!white,draw=green!60!black,thick] (0,0) circle (3); % % \draw[very thick,->] (-3.8,0) -- (3.8,0); % \draw[very thick,->] (0,-3.8) -- (0,3.8); % \node[anchor=south] at (3.8,0) {$x$}; % \node[anchor=west ] at (0,3.8) {$y$}; % % \coordinate (O) at (0,0); % \coordinate (A) at (#1:3); % \coordinate (B) at (#2:3); % % \filldraw[fill=green!90!black,thick] (0,0) -- (A) arc(#1:#2:3) -- (0,0); % \node at ($(A)+(#1:0.2)$) {$a$}; % \node at ($(B)+(#2:0.2)$) {$b$}; % % \draw[dashed,thick] (A) -| (O) (B) -| (O); %} %\begin{document} % \begin{tikzpicture} % \begin{scope} % \suika{-75}{-30}; \node[anchor=north] at (0,-4) {Figure 1}; % \end{scope} % \begin{scope}[xshift=8cm] % \suika{-75}{ 30}; \node[anchor=north] at (0,-4) {Figure 2}; % \end{scope} % \begin{scope}[xshift=16cm] % \suika{ 25}{ 54}; \node[anchor=north] at (0,-4) {Figure 3}; % \end{scope} %\end{tikzpicture} %\end{document} $$#include<bits/stdc++.h> #define up(l,r,i) for(int i=l,END##i=r;i<=END##i;++i) #define dn(r,l,i) for(int i=r,END##i=l;i>=END##i;--i) using namespace std; const double pi =acos(-1); double l,r; void slv(double s,double t,bool f){ //l/r if(t<=0.5*pi){ if(f) l+=sin(s),r+=sin(t); else l+=(sin(t)-sin(s)),r+=1; }else if(0.5*pi<=s){ if(f) l+=sin(s),r+=sin(s); else r+=1; } else{ if(f) l+=sin(s),r+=1; else l+=max(0.0,sin(t)-sin(s)),r+=max(sin(s),sin(t)); } } int main(){ int T; scanf("%d",&T); up(1,T,TT){ double a,b; scanf("%lf%lf",&a,&b); l=r=0,a=pi*a/180,b=pi*b/180; if(a<=pi&&b<=pi){ if(a<b) slv(a,b,0),r+=1; else slv(b,a,1); } else if(a>pi&&b>pi){ if(a<b) slv(2*pi-b,2*pi-a,0),r+=1; else slv(2*pi-a,2*pi-b,1); } else { if(a<b) slv(a,pi,0),slv(2*pi-b,pi,0); else slv(0,b ,0),slv(0,2*pi-a,0); } printf("%.1lf%%\n",100.0*l/r); } return 0; } - 第一类: 。观察下面三张图:
- 1
信息
- ID
- 2749
- 时间
- 1000ms
- 内存
- 125MiB
- 难度
- 5
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
