自动搬运

查看原文

来自洛谷，原作者为

	getchar123 即使遍体鳞伤，也永远不会服软

搬运于2025-08-24 21:52:26，当前版本为作者最后更新于2019-07-31 09:11:03，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

这题可以O($n^2$)过，以下是O（$n^2$)思路：

暴力枚举删掉的边，使它分成两棵树，然后考虑连接哪两个点可以使最大交通费用最小

这时有两种情况：

1.要最大交通费用的两个点在同一棵树上

2.最大费用的两个点分别在两棵树上

第一种情况是不会被连接的边影响的，我们要想办法连边让第二种情况的最大费用最小。显然是连接两棵树上直径的中点（这里别的题解都讲得比较详细，就不再赘述了）

重点来了：如何优化到O(n)

回顾O（$n^2$）的写法：在每去掉一条边后都分别在两棵树上用两遍bfs求树的直径。事实上只分别用一遍就行了。对于一棵被分割出来的树，它直径的一端一定是未删边时树的直径的一端。

反证：（此时a->d为原树上直径，b->e为要删的边）假设x1>x2，那么x1+y+z>x2
+y+z，则原树上直径为c->d，与条件矛盾。所以a距离b最远，a为新树上半径一端
	得证

优化后的时间复杂度依然达不到O（n），继续优化剩下一遍bfs：

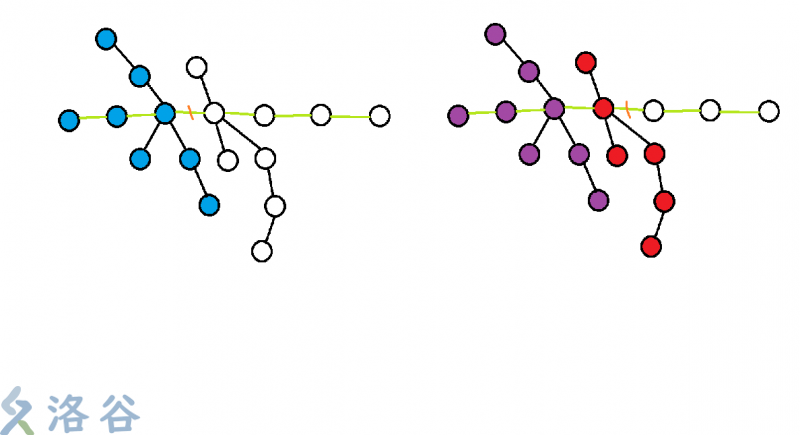
(橙色为截掉的边，绿色为直径，左边蓝色为遍历到的点右边红色为遍历一遍的点，紫色为重复遍历的点)可以看到，在枚举删边时有很多点被重复遍历到了。可以考虑第二次只遍历红色部分。这样总共只将树遍历了一遍，可以达到O（n）。

遍历到叶节点时更新直径（为了表述方便，所有边长度为1）（左边新树直径4，右边6）

维护直径中点

求出直径后，要寻找直径中点，此时如果遍历直径求中点，在极端情况下，时间复杂度还是O（$n^2$)。但可以发现，直径长度是单调不减的，因此半径长度也单调不减。可以由上次的中点推出这次的中点。

讲解瞎说时间到此结束

下面来梳理一遍思路

1. 求出原树上直径，记端点为r，l
2. 从直径左侧开始
3. 在直径上截边，遍历新增子树，更新直径
4. 上一次的中点后移，作为这一次中点
5. 更新半径
6. 存储信息
7. 重复步骤3-6，直到遍历完整个直径
8. 右侧同理
9. 扫描所有存储的信息，求出最终答案

代码

#include<bits/stdc++.h>
using namespace std;
struct bbbb{
	int to,nextt,xx;
}b[10010];
int n,tail,dd[5010],dis[5010],vis[5010],ldd,rdd,diss[5010],ttll;
struct llbb{
	int xxx,x;
}lb[5010];
struct cccc{
	int zjcd,bjcd,zd;
}cc1[5010],cc2[5010];
void jb(int x,int y,int z){
	tail++;
	b[tail].nextt=dd[x];
	b[tail].to=y;
	b[tail].xx=z;
	dd[x]=tail;
	return;
}
queue<int>q; 
void bfs(int x){
	memset(vis,0,sizeof(vis));
	dis[x]=0;
	vis[x]=1;
	q.push(x);
	while(q.empty()==false){
		int xx=q.front();q.pop();
		for(int i=dd[xx];i!=0;i=b[i].nextt){
			if(vis[b[i].to]==0){
				vis[b[i].to]=1;
				dis[b[i].to]=dis[xx]+b[i].xx;
				q.push(b[i].to);
			}
		}
	} 
	return;
}
bool dfs(int x,int mb){
	if(x==mb){
		ttll++;
		lb[ttll].x=x;
		return true;
	}
	for(int i=dd[x];i!=0;i=b[i].nextt){
		if(vis[b[i].to]==0){
			vis[b[i].to]=1;
			if(dfs(b[i].to,mb)==true){
				ttll++;
				lb[ttll].x=x;
				lb[ttll].xxx=b[i].xx;
				return true;
			}
		}
	}
	return false;
}
int bfs1(int x){
	int maxx=0;
	q.push(x);
	while(q.empty()==false){
		int xx=q.front();q.pop();
		maxx=max(maxx,diss[xx]);
		for(int i=dd[xx];i!=0;i=b[i].nextt){
			if(vis[b[i].to]==0){
				vis[b[i].to]=1;
				diss[b[i].to]=diss[xx]+b[i].xx;
				q.push(b[i].to);
			}
		}
	} 
	return maxx;
}
int main(){
	scanf("%d",&n);
	for(int i=1;i<n;i++){
		int x,y,z;
		scanf("%d%d%d",&x,&y,&z);
		jb(x,y,z);
		jb(y,x,z);
	}
	bfs(1);
	for(int i=1;i<=n;i++){
		if(dis[ldd]<=dis[i]){
			ldd=i;//左端点 
		}
	}
	bfs(ldd);
	for(int i=1;i<=n;i++){
		if(dis[rdd]<=dis[i]){
			rdd=i;//右端点 
		}
	}
	memset(vis,0,sizeof(vis));
	vis[ldd]=1;
	dfs(ldd,rdd);//存储树的直径 
//-------------上面是树的直径部分-----------------
	memset(vis,0,sizeof(vis));
	for(int i=1;i<=ttll;i++){
		vis[lb[i].x]=1;
	}
	int zhongd=1;
	for(int i=2;i<=ttll;i++){
		diss[lb[i].x]=diss[lb[i-1].x]+lb[i].xxx;
		int qwq=bfs1(lb[i].x);//遍历新子树 
		if(qwq<=cc1[lb[i-1].x].zjcd){
			cc1[lb[i].x]=cc1[lb[i-1].x];
		}
		else{
			while(zhongd<i&&max(diss[lb[zhongd].x],qwq-diss[lb[zhongd].x])>max(diss[lb[zhongd+1].x],qwq-diss[lb[zhongd+1].x])){
				zhongd++;//中点后移 
			}
			cc1[lb[i].x].zjcd=qwq;//更新直径 
			cc1[lb[i].x].bjcd=max(diss[lb[zhongd].x],qwq-diss[lb[zhongd].x]);//更新半径 
		}
	}
	memset(vis,0,sizeof(vis));
	memset(diss,0,sizeof(diss));
	for(int i=1;i<=ttll;i++){//右侧同理 
		vis[lb[i].x]=1;
	}
	zhongd=ttll;
	for(int i=ttll-1;i>=1;i--){
		diss[lb[i].x]=diss[lb[i+1].x]+lb[i+1].xxx;
		int qwq=bfs1(lb[i].x);
		if(qwq<=cc2[lb[i+1].x].zjcd){
			cc2[lb[i].x]=cc2[lb[i+1].x];
		}
		else{
			while(zhongd>i&&max(diss[lb[zhongd].x],qwq-diss[lb[zhongd].x])>max(diss[lb[zhongd-1].x],qwq-diss[lb[zhongd-1].x])){
				zhongd--;
			}
			cc2[lb[i].x].zjcd=qwq;
			cc2[lb[i].x].bjcd=max(diss[lb[zhongd].x],qwq-diss[lb[zhongd].x]);
		}
	}
	int minn=1e9;
	for(int i=1;i<ttll;i++){//扫描,求出最终答案 
		minn=min(minn,max(cc1[lb[i].x].bjcd+cc2[lb[i+1].x].bjcd+lb[i+1].xxx,max(cc1[lb[i].x].zjcd,cc2[lb[i+1].x].zjcd)));
	}
	printf("%d",minn);
	return 0;		
}

-end-

p.s.如果哪里不是很清楚，欢迎私信提建议哦~